ПРИМЕНЕНИЕ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ ДЛЯ РЕШЕНИЯ ДИНАМИЧЕСКИХ ЗАДАЧ
Литвинова Э.В.
ORCID: 0000–0001–5549–5627, кандидат технических наук,
Академия строительства и архитектуры
ФГАОУ ВО «КФУ имени В.И. Вернадского»
ПРИМЕНЕНИЕ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ ДЛЯ РЕШЕНИЯ ДИНАМИЧЕСКИХ ЗАДАЧ
Аннотация
Предлагается применение метода конечных разностей для решения динамических задач строительной механики на примере динамического изгиба жестко защемленной призматической балки под действием внезапно приложенной равномерно распределенной нагрузки, неизменной во времени. В методе конечных разностей область непрерывного изменения аргумента заменяется конечным (дискретным) множеством узлов, называемым сеткой. Метод конечных разностей – сеточный метод, основанный на замене производных разностными отношениями, прост и удобен для вычислений.
Ключевые слова: метод конечных разностей, сеточные функции, разностная схема, динамическое приложение нагрузки.
Litvinova E.V.
ORCID: 0000–0001–5549–5627, PhD in Engineering, Academy of Construction and Architecture V.I. Vernadsky Crimean Federal University
APPLICATION OF FINITE DIFFERENCES METHOD FOR DYNAMIC PROBLEMS SOLUTION
Abstract
The article proposes the application of finite differences method for solving the dynamic problems of building mechanics with the help of dynamic bending of a rigidly clamped prismatic beam under the impact of a suddenly applied uniformly distributed load, unchanged in time. In the method of finite differences, the domain of continuous change of the argument is replaced by a finite (discrete) set of nodes, called a grid. Finite differences method – the grid method, based on the replacement of derivatives by differencing ratios, is simple and convenient for calculations.
Keywords: finite difference method, grid functions, differencing scheme, dynamic load application.
Решение сложных инженерных задач, относящихся к предметной области науки о прочности и устойчивости строительных конструкций, существенно упрощается благодаря моделированию. Математические модели строительных конструкций представляют собой условия равновесия конструкций и ее узлов, выраженные в дифференциальной или интегральной форме, под действием различного рода нагрузок.
Рассмотрим один из методов дискретизации аналитических моделей функционирования строительных конструкций – метод конечных разностей (МКР).
Пусть на отрезке ![]() требуется найти решение некоторого уравнения
требуется найти решение некоторого уравнения
![]()
где L – некоторый дифференциальный оператор.
Будем предполагать, что решение ![]() уравнения (1) имеет необходимое число производных. Для его решения применим МКР [1 – 3].
уравнения (1) имеет необходимое число производных. Для его решения применим МКР [1 – 3].
В МКР область непрерывного изменения аргумента заменяется конечным (дискретным) множеством узлов, называемым сеткой. Сетку вводят следующим образом. Отрезок изменения аргумента ![]() разбивают на n равных частей длиной
разбивают на n равных частей длиной ![]() каждая. Сами точки
каждая. Сами точки ![]() называются узлами сетки. На сетке вместо функции непрерывного аргумента
называются узлами сетки. На сетке вместо функции непрерывного аргумента ![]() рассматриваются функции дискретного аргумента
рассматриваются функции дискретного аргумента ![]() , определяемые в узлах сетки и называемые сеточными функциями. Производные заменяются (аппроксимируются) соответствующими разностными отношениями, то есть линейной комбинацией значений сеточной функции в нескольких узлах [1, 3].
, определяемые в узлах сетки и называемые сеточными функциями. Производные заменяются (аппроксимируются) соответствующими разностными отношениями, то есть линейной комбинацией значений сеточной функции в нескольких узлах [1, 3].
Необходимо найти разностный аналог производной функции ![]() в касательной к кривой в точке. Это можно сделать с помощью замены истинной производной следующими разностными отношениями [3]:
в касательной к кривой в точке. Это можно сделать с помощью замены истинной производной следующими разностными отношениями [3]:

Первое выражение в (2) определяет левую одностороннюю разностную производную, второе выражение – правую одностороннюю разностную производную, третье – двусторонняя разностная производная.
Очевидно, располагая выражением для первой производной, можно выписать разностные аналоги и для производных высших порядков [3]:
![]()
Заменяя в дифференциальном уравнении производные их разностными аналогами, приходим к разностному уравнению относительно узловых неизвестных, которое вместе с разностными краевыми условиями, называют разностной схемой.
Часто при решении задач с помощью МКР (главным образом при аппроксимации граничных условий) используют правые и левые разности, аналогичные по точности аппроксимации центральным разностям. Приведем без вывода наиболее характерные из них [3]:
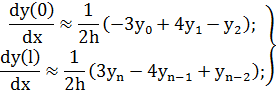
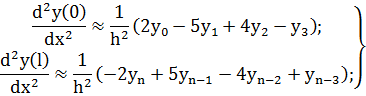
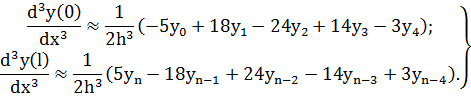
Для исключения грубых ошибок при построении разностных схем полезно помнить, что сумма коэффициентов в рассмотренных выражениях для разностных аналогов производных, должна равняться нулю.
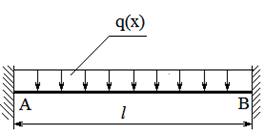
Рис. 1 – Схема крепления и нагружения балки
Применение МКР для решения динамических задач покажем на примере динамического изгиба жестко защемленной призматической балки (рис. 1), под действием внезапно приложенной равномерно распределенной нагрузки, неизменной во времени ![]() Здесь
Здесь ![]() – единичная функция Хэвисайда
– единичная функция Хэвисайда
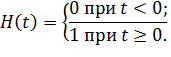
Схема задачи, показанная на рис. 1, отличается в динамическом приложении нагрузки. До приложения нагрузки балка неподвижна и не имеет прогиба.
Динамика системы с внезапным приложением нагрузки описывается дифференциальным уравнением
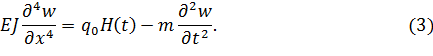
Здесь: ![]() – погонная масса; ρ – плотность материала; А – площадь поперечного сечения; Е – модуль Юнга; J – момент инерции поперечного сечения; w – величина прогиба балки; x – горизонтальная координата вдоль оси балки.
– погонная масса; ρ – плотность материала; А – площадь поперечного сечения; Е – модуль Юнга; J – момент инерции поперечного сечения; w – величина прогиба балки; x – горизонтальная координата вдоль оси балки.
Если предположить, что колебания системы происходят при наличии сил сопротивления, пропорциональных скорости движения поперечных сечений балки, то уравнение (3) можно записать так
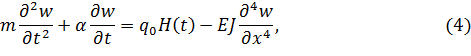
где α – коэффициент сопротивления. Уравнение (3) необходимо дополнить начальными и граничными условиями:
![]()
![]()
Применим для решения краевой задачи (4) – (6) МКР. Выберем на плоскости ![]() (
( ![]() – координата,
– координата, ![]() – время) прямоугольную равномерную сетку с шагами
– время) прямоугольную равномерную сетку с шагами ![]() и
и ![]() . Искомые сеточные функции
. Искомые сеточные функции ![]() (j – номер шага по координате x, i – номер шага по времени t,
(j – номер шага по координате x, i – номер шага по времени t, ![]() – итоговая функция прогиба балки). Для аппроксимации производных, входящих в уравнение (4), а также граничных и начальных условий применим формулы центральных конечных разностей:
– итоговая функция прогиба балки). Для аппроксимации производных, входящих в уравнение (4), а также граничных и начальных условий применим формулы центральных конечных разностей:
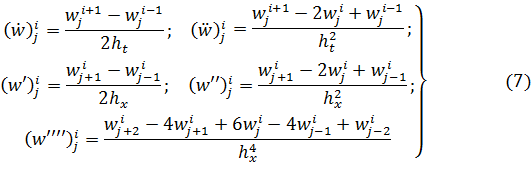
Разделим (4) на массу m
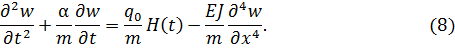
Подставим выражения (7) и граничные условия (5) и (6) в уравнение (8). Получим систему алгебраических уравнений относительно сеточных функций![]() внутри области
внутри области ![]() в момент времени i
в момент времени i
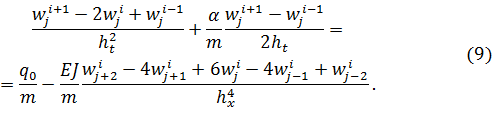

Рис. 2 – Двумерная разностная сетка
Как видно из выражения (9), в точке на плоскости ![]() с координатами (j, i) ее прогиб формируется с помощью семи узловых точек, образующих на плоскости «крест» (рис. 2). При этом значение узловой переменной на новом шаге по времени
с координатами (j, i) ее прогиб формируется с помощью семи узловых точек, образующих на плоскости «крест» (рис. 2). При этом значение узловой переменной на новом шаге по времени ![]() может быть явно выражено из уравнения (9). Поэтому разностную схему (9), построенную с помощью соотношений (7) называют явной разностной схемой типа «крест»
может быть явно выражено из уравнения (9). Поэтому разностную схему (9), построенную с помощью соотношений (7) называют явной разностной схемой типа «крест»
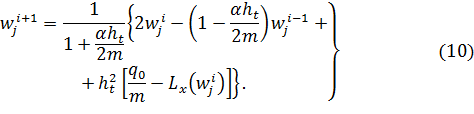
Здесь
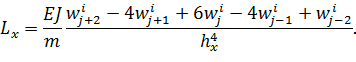
Граничные условия (6) не зависят от времени и могут быть записаны следующим образом:
![]() (11)
(11)
Из начальных условий (5) имеем
![]()
Для замыкания системы нам необходимо получить значения узловых перемещений ![]() на первом шаге по времени (i = 1). Они могут быть найдены при помощи разложения в ряд Тейлора с учетом начальных условий (10)
на первом шаге по времени (i = 1). Они могут быть найдены при помощи разложения в ряд Тейлора с учетом начальных условий (10)
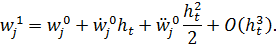
Для определения ![]() воспользуемся уравнением (8). Тогда
воспользуемся уравнением (8). Тогда
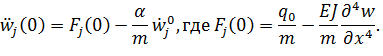
Отсюда следует, что ![]()
Таким образом, имеем разностное уравнение (10), граничные условия (11) и начальные условия для первого и второго слоя разностной схемы
![]()
которые аппроксимируют краевую задачу (8) с граничными и начальными условиями с точностью до величины ![]()
Определим прогиб балки, что позволит получить сравнительный анализ напряженно–деформированного состояния конструкции при статическом и динамическом видах нагружения. В качестве динамической нагрузки примем равномерно распределенную нагрузку, но приложенную внезапно. В этом случае коэффициент динамичности равен двум.
Кроме того, не будем учитывать внутреннее сопротивление конструкции. Тогда уравнение движения балки (4) примет вид
![]()
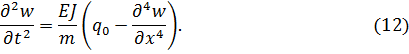
Здесь ![]()
Зададим исходные данные: ![]() – погонная нагрузка,
– погонная нагрузка, ![]() − длина балки,
− длина балки, ![]() − модуль упругости,
− модуль упругости, ![]() − допускаемое напряжение.
− допускаемое напряжение.
Максимальный изгибающий момент в месте жесткой заделки балки ![]() Допускаемый момент сопротивления для данных условий составляет
Допускаемый момент сопротивления для данных условий составляет ![]() Пусть балка имеет двутавровое сечение. Тогда из таблицы сортаментов выбираем двутавр № 18, для которого:
Пусть балка имеет двутавровое сечение. Тогда из таблицы сортаментов выбираем двутавр № 18, для которого: ![]() − площадь поперечного сечения. Погонная масса балки при значении плотности материала
− площадь поперечного сечения. Погонная масса балки при значении плотности материала ![]() составляет
составляет ![]() Прогиб балки при статической нагрузке в фиксированных сечениях составляет:
Прогиб балки при статической нагрузке в фиксированных сечениях составляет:
![]()
Перейдем к динамическому расчету. Разобьем балку по длине на пять равных отрезков ![]()
Применим МКР к уравнению (12), получим четыре уравнения:
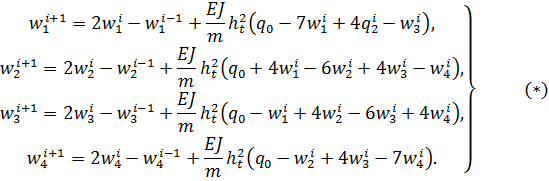
Систему (*) удобно решать на ПК, причем в начальный момент времени все прогибы равны нулю. В результате расчета колебательного процесса без затухания получены максимальные значения прогибов балки в соответствующих ее сечениях: ![]() Обозначенные прогибы в два раза больше, чем при статической нагрузке, то есть соответствуют коэффициенту динамичности.
Обозначенные прогибы в два раза больше, чем при статической нагрузке, то есть соответствуют коэффициенту динамичности.
Вполне естественно, что максимальный изгибающий момент в заделке балки должен быть в два раза больше, т. е. ![]()
![]()
С целью обеспечения прочности балки при заданной динамической нагрузке необходимо определить допускаемый момент сопротивления сечения ![]()
![]() . Из сортамента выбираем двутавр № 22а:
. Из сортамента выбираем двутавр № 22а: ![]() При таких условиях решение динамической задачи дает:
При таких условиях решение динамической задачи дает: ![]()
При этом ![]()
Таким образом, условия прочности удовлетворяются.
Рассматриваемая схема проста и удобна для вычислений.
Список литературы / References
- Курамшина Р.П. Численные методы в строительстве и их реализация: учебное пособие / Р.П. Курамшина. – Братск: ГОУВПО «Братский государственный университет», 2010. – 104 с.
- Чемодуров В.Т. Методы теории планирования эксперимента в решении технических задач: монография / В.Т. Чемодуров, В.В. Жигна. – Симферополь: ИТ «АРИАЛ», 2012. – 110 с.
- Чемодуров В.Т. Численные методы в строительстве: учебное пособие / В.Т. Чемодуров, М.С. Сеитжелилов. – Симферополь: ИТ «АРИАЛ», 2016. – 112 с.
Список литературы на английском языке / References in English
- Kuramshina R.P. Chislennye metody v stroitel'stve i ih realizacija: uchebnoe posobie [Numeral methods in building and their realization: train aid] / R.P. Kuramshina. – Bratsk: GOUVPO «Bratskij gosudarstvennyj universitet» [Bratsk State University], 2010. – 104 p. [in Russian]
- Chemodurov V.T. Metody teorii planirovanija jeksperimenta v reshenii tehnicheskih zadach: monografija [Methods of theory of planning of experiment are in the decision of technical tasks: monograph] / V.T. Chemodurov, V.V. Zhigna. – Simferopol': IT «ARIAL», 2012. – 110 p. [in Russian]
- Chemodurov V.T. Chislennye metody v stroitel'stve (dlja studentov vseh special'nostej ochnoj i zaochnoj form obuchenija): uchebnoe posobie [Numeral methods are in building: train aid] / V.T. Chemodurov, M.S. Seitzhelilov. – Simferopol': IT «ARIAL», 2016. – 112 p. [in Russian]
