МОДЕЛИРОВАНИЕ ВОЗДЕЙСТВИЯ АГРАРНОГО СЕКТОРА ЭКОНОМИКИ НА КАЧЕСТВО ОКРУЖАЮЩЕЙ СРЕДЫ

Зарецкая М.В.

ORCID: 0000-0002-9857-2693, Доктор физико-математический наук, доцент, Кубанский государственный университет

Работа выполнена при поддержке РФФИ (грант № 16-08-00191_а), РФФИ и администрации Краснодарского края (грант № 16-41-230154)

МОДЕЛИРОВАНИЕ  ВОЗДЕЙСТВИЯ АГРАРНОГО СЕКТОРА ЭКОНОМИКИ НА КАЧЕСТВО ОКРУЖАЮЩЕЙ СРЕДЫ

Аннотация

В настоящей статье представлены математические модели, включение которых в системы комплексного экологического мониторинга и производственного контроля позволит дать динамический прогноз состояния экологической системы в зоне агропромышленного предприятия до, во время и после производственного процесса.

Формулировка граничных задач выполнена на основе уравнений движения в различных системах координат. Физическая среда, в которой исследуются процессы, может  характеризоваться существенно отличающимися физико-механическими, химическими параметрами. Построение моделей базируется на топологическом подходе, включающем теорию блочных структур и дифференциальный метод факторизации.

Получены решения модельных задач.

Ключевые слова: аграрный сектор экономики, мониторинг, негативное воздействие, экология, качество среды, моделирование окружающей среды.

Zaretskaya M.V.

ORCID: 0000-0002-9857-2693, PhD in Physics and Mathematics, Associate Professor, Kuban State University

This work was supported by the Russian Foundation for Basic Research (Grant No. 16-08-00191_a), the RFBR and the Administration of the Krasnodar Region (grant No. 16-41-230154)

MODELING THE IMPACT OF AGRARIAN SECTOR OF ECONOMICS ON THE QUALITY OF ENVIRONMENT

Abstract

This article presents mathematical models the inclusion of which into the systems of integrated environmental monitoring and production control will enable giving a dynamic forecast of the ecological system state in agro-industrial enterprise area before, during and after the production process.

Stating boundary problems is based on the equations of motion in various coordinate systems. Physical environment where the processes are studied can be characterized by substantially different physical, mechanical and chemical parameters. The construction of models is based on a topological approach, including the theory of block structures and the differential factorization method.

Solutions of model problems are obtained.

Keywords: agrarian sector of economy, monitoring, negative impact, ecology, quality of environment, environmental modeling.

Введение

Отличительной особенностью сельскохозяйственного производства является наличие взаимно-однозначных связей с геоэкологической средой. Подвергаясь разнотипному влиянию со стороны внешнего окружения, предприятия агропромышленного комплекса в свою очередь формируют качество экологической системы,  оказывая на нее существенное, длительное, иногда определяющее, воздействие, отличающееся интенсивностью, разнотипностью форм и масштабов, что обусловлено высокой токсичностью и большим разнообразием химических субстанций, используемых в производственных процессах.

Негативному воздействию со стороны элементов сельскохозяйственного производства подвергаются  почвы, атмосфера, поверхностные и подземные воды.

С другой стороны, став действующим фактором в результате вторичного переноса, оседающие загрязняющие вещества могут стать причиной токсичного  или  радионуклеидного заражения,  изменения химического состава почв, оказать мутагенное воздействие на  сельскохозяйственные культуры.

Существуют два пути разработки современных систем экологического мониторинга в агропромышленном производстве, как основного инструмента оценки качества окружающей  среды в зоне возможного влияния агропромышленного предприятия [1].

Прежде всего, это  химико-аналитический контроль. Такая система располагает широкой базой информационных ресурсов, развитыми методами и методиками инструментального аналитического контроля, результатами длительного экологического мониторинга  показателей окружающей  среды, определяющих ее  качество.

Однако существующая экологическая обстановка в регионах интенсивного аграрного производства свидетельствует о недостаточности мер регулирования природопользования на уровне законодательства. Экологический мониторинг и производственный контроль, как наиболее часто используемый инструмент наблюдения за уровнем негативных последствий  агропромышленного производства, выполняет функцию  фиксации  текущих значений параметров и процессов. Он не обеспечивает в полной мере проведения экологической оценки состояния экосистем и диагностики дальнейшего развития событий, не позволяет проследить динамические изменения в уровне основных оцениваемых параметров, и  не обладает прогностической значимостью.

Поэтому перед разработчиками встает необходимость и потребность включения в системы комплексного экомониторинга математических модулей, позволяющих дать динамический прогноз состояния экологической системы в зоне агропромышленного предприятия до, во время и после производственного процесса.

Математическая модель. Методы решения

Перенос загрязняющих субстанций (СБ) – сложный процесс, существенно определяемый динамическими процессами в атмосфере и водной среде. Также необходимо учитывать термодинамические характеристики,  природный и промышленный ландшафт,  и  т.д. [2], [3], [4]. Рассмотрим основные механизмы.

В настоящее время получили развитие различные математические подходы, статистические, аналитические, численные, анализа процессов переноса в некоторой среде.

Наиболее достоверными  считаются  модели, построение которых базируется на решении трехмерного нелинейного уравнения турбулентной диффузии [2], [3].  Несомненным достоинством методов,  предложенных в [2], [3], является учет физико-химических трансформаций и взаимодействия субстанций, которые свойственны реальным процессам переноса. При всех достоинствах эти модели не лишены недостатков. Один из  наиболее существенных – применение численных методов, которые позволяют получить решение в узлах сетки, при этом некоторые особенности процессов, особенно на мезомасштабном уровне, могут быть утеряны.

В связи с широким распространением в природе циклонических (конвективных) движений [1], [4], требуется развитие теории и методов исследования переноса ЗВ при одновременном наличии плоскопараллельных и  конвективных течений. Выполним постановки задач переноса.

1. Транспорт субстанций плоскопараллельным течением.

Считаем, что перенос субстанций в атмосфере или водной среде описывается уравнением переноса [2], [3], [4], распределение физико-механических характеристик среды по вертикали таково, что ее можно аппроксимировать однородными слоями с  установившимся движением , где каждый слой может иметь свои, в общем случае различные  характеристики .

Распространение вещества  в каждом слое описывается уравнением:

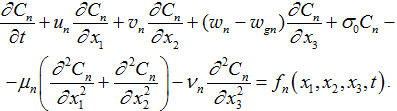  (1)

Обозначения и физико-механический смысл коэффициентов уравнения (1) определены в [4, 5].

СБ оседает  на поверхность Ω, являющуюся , соотносящиеся с конкретными ландшафтами территории: участки сельскохозяйственных полей и насаждений,  лесополосы, и т.д. [5].

На нижней границе пакета слоев  в каждой области Ω_l ставится граничное условие

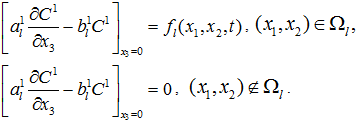
Здесь  – параметры граничных условий; функция  может моделировать сброс в водоем сточных вод, выбросы труб промышленных предприятий. В случае площадного источника она моделирует, например, автомагистраль, являющуюся источником продуктов горения бензина, тяжелых металлов, которые переносятся и осаждаются на поля, или, наоборот,  сельскохозяйственное   угодье, с которого происходит сдув ядохимикатов, удобрений.

2. Транспорт примесей свободными или вынужденными конвективными потоками.

Уравнения переноса,  в цилиндрической системе координат  имеют вид

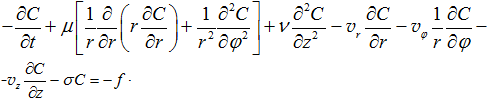
Для постановки граничных условий считаем, что с цилиндрической поверхности находящейся в конвективном движении области среды происходит приток загрязняющего вещества:

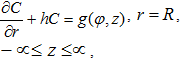
где  задает концентрацию примеси на цилиндрической поверхности ячейки, h – параметр, характеризующий эффективность обмена между ячейкой и окружающей средой.

Формулировка задач (1) – (2) выполнена на основе уравнений движения в различных системах координат [6]. Физическая среда, в которой исследуется процесс переноса, может  характеризоваться существенно отличающимися физико-механическими, химическими параметрами. Сложность постановки делает необходимым применение топологического подхода, реализуемого в форме метода блочного элемента, и факторизационных методов [7].

Моделирование отдельных ситуаций

Рассмотрены три задачи.

1. Оценка сноса некоторой СБ воздушным потоком, например, ядохимикатов при распылении с самолета.

При штатной ситуации вся масса субстанции концентрируется на обрабатываемом поле. Оседание происходит неравномерно, выделяются зоны повышенной концентрации, в том числе, превосходящие ПДК. Возможно смещение области максимальной концентрации на прилегающую территорию. Также в зависимости от скорости ветра наблюдались следы ненулевой концентрации на расстоянии от 5 до 28 км от обрабатываемого поля.

2. Оценка сноса СБ от точечного поверхностного источника постоянной мощности, который моделирует, например, стационарные выбросы завода по переработке. Полученные результаты закономерны – зона оседания формируется на некотором расстоянии, зависящем от скорости ветра, от источника. Особенно сложная картина наблюдается, если кроме плоскопараллельного ветрового потока присутствуют восходящие конвективные вихри. В этом случае примесь попадает в верхние слои приземного слоя, которые характеризуются изменением направления и интенсивности потока, и оседает в значительно удаленных областях. Предугадать такой результат без математического моделирования было бы невозможно.
3. Моделирование вторичного переноса облака от выброса точечного источника при оседании на водную поверхность. Результаты зависят от типа СБ (легкая или тяжелая) и структуры водных течений. При наличии только плоскопараллельных течений происходит снос легкой СБ с постепенным уменьшением концентрации. Формируется область поражения до 4–18 км. Тяжелая СБ оседает на дно, формируя четко выраженную зону с фиксированной точкой максимального значения. При наличии горизонтального или вертикального конвективного течения теряется четкость очертания зоны загрязнения, формируются кольцевые структуры. Результаты хорошо согласуются с данными исследования переноса продуктов грязевулканической деятельности в Азовском море [8].

Проведение расчетов для  различных сценариев температурно-климатических условий позволяет оптимизировать результаты процесса и исключить возможность заражения прилегающих и удаленных территорий.

Заключение

Особенностью топологических методов является возможность получить решение задач в интегральном представлении и сделать выводы о свойствах исследуемых процессов без вычисления интегралов, что существенно уменьшает время расчетов и способствует созданию основ новых перспективных технологий экологического мониторинга, контроля и управления качеством водной среды или атмосферного воздуха.

Построенные математические модели могут быть реализованы при решении следующих научно-практических задач:

1. Динамическая оценка поступления вредных веществ в окружающую среду в результате деятельности предприятий агропромышленного комплекса;
2. Оценка последствий выбросов, в том числе, отдаленных, предприятиями аграрного сектора экономики загрязняющих веществ, включая тяжелые, радиоактивные, токсичные: загрязнение атмосферного воздуха и континентальных водоемов;
3. Оценка последствий применения современных способов переработки отходов сельского хозяйства (сжигание или захоронение органических отходов, анаэробной обработки отходов с получением биогаза, тепловой, электрической энергии);
4. Прогноз загрязнения и деградации сельскохозяйственных земель вследствие выбросов промышленности и транспорта, радиоактивного загрязнения;
5. Загрязнение водных ресурсов, используемых в сельском хозяйстве, стоками промышленности и жилищно-коммунального хозяйства.

Список литературы / References

1. Зарецкая М.В. Математический аппарат исследования блочных структур с разнотипными блоками / М.В. Зарецкая, А.Г.Зарецкий // Международный научно-исследовательский журнал. – 2016.– № 3 (45).  Часть 2. – С. 58–60.
2. МарчукГ.И. Математическое моделирование в проблеме окружающей среды / Г.И. Марчук. – М.: Наука, 1982.– 320 с.
3. Алоян А.Е. Моделирование динамики и кинетики газовых примесей и аэрозолей в атмосфере / А.Е. Алоян. – М.: Наука, 2008. – 415 с.
4. Бабешко В.А. К вопросу моделирования процессов переноса в экологии, сейсмологии и их приложения / В.А. Бабешко, М.В. Зарецкая, И.В. Рядчиков // Экологический вестник научных центров Черноморского экономического сотрудничества. – 2008.– № 3. – С. 20–25.
5. Зарецкая М.В. Исследование влияния разнотипности подстилающих поверхностей на процесс массопереноса в слоисто-неоднородных средах / М.В. Зарецкая // Экологический вестник научных центров Черноморского экономического сотрудничества. – 2003. – № 1. – С. 42.
6. Babeshko V.A. Block elements with a cylindrical boundary in macro-and nanostructures / V.A. Babeshko, O.V. Evdokimova, O.M. Babeshko // Doklady Physics. – 2011. – Volume 56. Issue 10. – Pages 544–547.
7. Babeshko V.A. The differential factorization method for a block structure / V.A. Babeshko, O.V. Evdokimova, O.M. Babeshko, M.V. Zaretskaya, A.V. Pavlova // Doklady Physics. – 2009. – Volume 54. Issue 1. – Pages 25–28.
8. Зарецкая М.В., Бабешко В.А., Ратнер С.В. Моделирование процесса переноса в водной среде продуктов грязевулканической деятельности // Защита окружающей среды в нефтегазовом комплексе. – 2008. – № 11. – С. 27–29.

Список литературы на английском языке / References in English

1. Zareckaja M.V. Matematicheskij apparat issledovanija blochnyh struktur s raznotipnymi blokami [Mathematical apparatus for studying block structures with different types of blocks] / M.V. Zareckaja, A.G. Zareckij // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. – 2016. – № 3 (45). Chast' 2. – P. 58–60. [in Russian]
2. Marchuk G.I. Matematicheskoe modelirovanie v probleme okruzhajushhej sredy [Mathematical modeling in the environmental problem] / G.I. Marchuk. – M.: Nauka, 1982. – 320 P. [in Russian]
3. Alojan A.E. Modelirovanie dinamiki i kinetiki gazovyh primesej i ajerozolej v atmosfere [Modeling of dynamics and kinetics of gas impurities and aerosols in the atmosphere] / A.E. Alojan. – M.: Nauka, 2008. – 415 P. [in Russian]
4. Babeshko V.A. K voprosu modelirovanija processov perenosa v jekologii, sejsmologii i ih prilozhenija [To the problem of modeling transport processes in ecology, seismology and their applications] / V.A. Babeshko, M.V. Zareckaja, I.V. Rjadchikov // Jekologicheskij vestnik nauchnyh centrov Chernomorskogo jekonomicheskogo sotrudnichestva [Ecological bulletin of scientific centers of the Black Sea Economic Cooperation]. – 2008.– № 3.– P. 20–25. [in Russian]
5. Zareckaja M.V. Issledovanie vliyaniya raznotipnosti podstilayushchih poverhnostej na process massoperenosa v sloisto-neodnorodnyh sredah [Investigation of the influence of the heterogeneity of the underlying surfaces on the process of mass transfer in layered inhomogeneous media]/ M.V. Zareckaja // Jekologicheskij vestnik nauchnyh centrov Chernomorskogo jekonomicheskogo sotrudnichestva [Ecological bulletin of scientific centers of the Black Sea Economic Cooperation]. – 2003. – № 1. – P. 42. [in Russian]
6. Babeshko V.A. Block elements with a cylindrical boundary in macro-and nanostructures / V.A. Babeshko, O.V. Evdokimova, O.M. Babeshko // Doklady Physics. – 2011. – Volume 56. Issue 10. – P. 544–547.
7. Babeshko V.A. The differential factorization method for a block structure / V.A. Babeshko, O.V. Evdokimova, O.M. Babeshko, M.V. Zaretskaya, A.V. Pavlova // Doklady Physics. – 2009. – Volume 54. Issue 1. – Pages 25–28.
8. Zareckaja M.V. Modelirovanie processa perenosa v vodnoj srede produktov grjazevulkanicheskoj dejatel'nosti [Modeling the process of transport in the aquatic environment of products of mud volcanic activity] / M.V. Zareckaja, V.A. Babeshko, S.V. Ratner // Zashhita okruzhajushhej sredy v neftegazovom komplekse [Environmental protection in the oil and gas sector]. – 2008. – № 11. – S. 27–29. [in Russian]