МОДЕЛИРОВАНИЕ ЭЛЕКТРОХИМИЧЕСКОЙ ОБРАБОТКИ ВРАЩАЮЩИМСЯ ПЛАСТИНЧАТЫМ ЭЛЕКТРОД-ИНСТРУМЕНТОМ
Житников В.П.1, Шерыхалина Н.М.2, Соколова А.А.3
1ORCID: 0000-0002-6198-0917, Доктор физико-математических наук,
Уфимский Государственный Авиационный Технический Университет,
2ORCID: 0000-0002-2808-1311, Доктор технических наук,
Уфимский Государственный Авиационный Технический Университет,
1ORCID: 0000-0002-1528-8778, Аспирант,
Уфимский Государственный Авиационный Технический Университет
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 17-07-00356).
МОДЕЛИРОВАНИЕ ЭЛЕКТРОХИМИЧЕСКОЙ ОБРАБОТКИ ВРАЩАЮЩИМСЯ ПЛАСТИНЧАТЫМ ЭЛЕКТРОД-ИНСТРУМЕНТОМ
Аннотация
Проведено моделирование способа электрохимической обработки вращающимся пластинчатым электродом-инструментом, который позволяет создать условия для постоянного обмена электролита. В качестве примера рассмотрена задача прорезания прямолинейных пазов. Для численного моделирования использован метод постоянных граничных элементов. Проведенное численное исследование позволило обнаружить и объяснить эффект образования волнообразной формы одной из боковых границ паза. Найдено условие, при котором амплитуда волн имеет наибольшее значение.
Ключевые слова: нестационарный процесс, метод граничных элементов, волнообразная форма границ.
Zhitnikov V.P.1, Sherykhalina N.M.2, Sokolova A.A.3
1ORCID: 0000-0002-6198-0917,
PhD in Physics and Mathematics, Ufa State Aviation Technical University,
2ORCID: 0000-0002-2808-1311,
PhD in Engineering, Ufa State Aviation Technical University,
3ORCID: 0000-0002-1528-8778, Postgraduate student,
Ufa State Aviation Technical University
The work was supported by the Russian Foundation for Basic Research (Project code 17-07-00356)
SIMULATION OF ELECTROCHEMICAL PROCESSING OF ROTATING PLATE ELECTRODE INSTRUMENT
Abstract
A simulation of the electrochemical machining method by a rotating plate electrode tool is carried out in this paper; it allows creating conditions for the permanent exchange of the electrolyte. The problem of straight lines cutting is considered as an example, the constant boundary elements method is used for numerical modeling. The performed numerical study made it possible to detect and explain the effect of the formation of a wave-shaped form of one of the lateral boundaries of the groove. It was found a condition under which the wave amplitude has the greatest value.
Keywords: nonstationary process, boundary elements method, wavy shape of boundaries.
Для получения штампов сложной формы из трудно обрабатываемых материалов часто используется электрохимическая обработка (ЭХО), которая имеет ряд важных преимуществ: отсутствие силового и теплового воздействия на обрабатываемую заготовку, отсутствие износа электрод-инструмента (ЭИ). В этом случае обычно используется ЭИ круглого сечения [1], [2], [3]. При этом во избежание загрязнения электролита продуктами реакций его прокачивают вдоль ЭИ. Для улучшения обмена электролита во фронтальной области межэлектродного пространства (МЭП) приходится периодически выключать напряжение, прерывая процесс растворения, и отводить ЭИ назад. Возможен другой тип технологического процесса. Если использовать ЭИ в виде узкой полосы, то вращение такого ЭИ будет создавать условия для постоянного обмена электролита.
Рассмотрим нестационарную задачу ЭХО с помощью пластинчатого ЭИ конечной толщины. Форма межэлектродного пространства показана на рис. 1. Центр ЭИ движется внутри заготовки со скоростью ![]() вниз вдоль оси ординат. Одновременно ЭИ вращается относительно своего центра с угловой скоростью ω. Начальное отверстие в заготовке имеет некоторую форму (обычно, круглую), разность потенциалов между электродами равна U.
вниз вдоль оси ординат. Одновременно ЭИ вращается относительно своего центра с угловой скоростью ω. Начальное отверстие в заготовке имеет некоторую форму (обычно, круглую), разность потенциалов между электродами равна U.
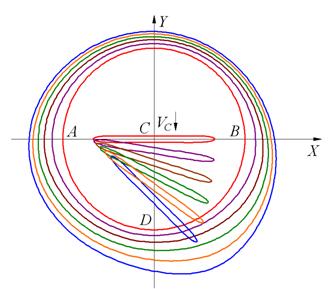
Рис. 1– Схема МЭП: ADB – обрабатываемая поверхность (анод); C – ЭИ (катод)
Процесс электрохимического растворения материала анода определяется законами Фарадея и Ома [4]
![]() (1)
(1)
где ![]() – скорость электрохимического растворения (сдвига границы); E, j – напряженность и плотность тока на границе анода;
– скорость электрохимического растворения (сдвига границы); E, j – напряженность и плотность тока на границе анода; ![]() – электропроводность электролита; η – выход по току; ε – электрохимический эквивалент; ρ – плотность растворяемого материала.
– электропроводность электролита; η – выход по току; ε – электрохимический эквивалент; ρ – плотность растворяемого материала.
Электрическое поле считается потенциальным и соленоидальным, поэтому потенциал ![]() удовлетворяет уравнению Лапласа
удовлетворяет уравнению Лапласа ![]() .
.
На границах, соответствующих электродам, значения потенциала на аноде и катоде равны
![]()
Перейдем к безразмерным величинам. Безразмерные величины x, y, τ и φ определяются следующим образом
![]()
где ![]() – величина стационарного зазора в задаче об обработке плоским горизонтальным ЭИ.
– величина стационарного зазора в задаче об обработке плоским горизонтальным ЭИ.
Центр ЭИ движется, как показано на рис. 1 со скоростью VC. При этом
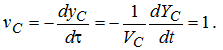
Граница детали также подвижна, нормальная скорость ее движения определяется уравнением (1). Представим (1) в безразмерном виде
![]() (2)
(2)
Здесь ![]() – координаты точек на обрабатываемой поверхности (ОП);
– координаты точек на обрабатываемой поверхности (ОП); ![]() – угол наклона внешней нормали к поверхности анода.
– угол наклона внешней нормали к поверхности анода.
Перемещение точек поверхности ЭИ в процессе обработки можно определить следующим образом
![]() (3)
(3)
где ![]() – координаты точек на исходной поверхности ЭИ (при
– координаты точек на исходной поверхности ЭИ (при ![]() );
); ![]() – угол поворота ЭИ вокруг своей оси относительно начального положения (на рис. 1 α изменяется от 0 до
– угол поворота ЭИ вокруг своей оси относительно начального положения (на рис. 1 α изменяется от 0 до ![]() ).
).
При численном решении безразмерное время дискретизируется, т. е. разбивается на некоторое количество шагов, на каждом шаге решается краевая задача для уравнения Лапласа
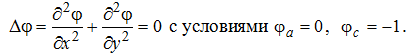 (4)
(4)
При этом определяются нормальные производные ![]() . Далее, согласно (2) и (3) производится шаг по времени (например, по методу Эйлера).
. Далее, согласно (2) и (3) производится шаг по времени (например, по методу Эйлера).
![]() (5)
(5)
![]() (6)
(6)
Далее процесс повторяется.
Решение краевой задачи для уравнения Лапласа с граничными условиями первого рода (4) на основе интеграла Грина сводится к граничному интегральному уравнению [1]
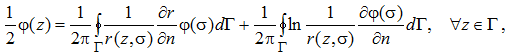 (7)
(7)
где z – точка наблюдения, σ – точка расположения источника; ![]() – расстояние между точкой наблюдения и источником; Г – граница области, проходимая так, что область находится слева.
– расстояние между точкой наблюдения и источником; Г – граница области, проходимая так, что область находится слева.
Для решения интегрального уравнения (7) будем использовать метод граничных элементов. Для упрощения расчетов, аналогично [1], будем использовать постоянные граничные элементы, в которых напряженность электрического поля имеет постоянные значения.
Разобьем границу Г на n прямолинейных граничных элементов Гm. Расчетные точки (узлы) расположим в середине граничного элемента. Дискретная форма уравнения (5а) будет иметь вид
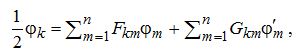 (8)
(8)
где
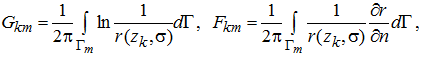 (9)
(9)
(при наличии особенности во втором интеграле в (9), согласно формуле Сохоцкого, берется его главное значение). Интегралы, входящие в (9), вычисляются точно.
Пусть расстояния от середины k-го элемента до начала и конца m-го элемента равны ![]() – углы между отрезками, соединяющими середину k-го граничного элемента с начальной и конечной точкой m-го граничного элемента, соответственно, и внешней нормалью к m-му граничному элементу при прохождении границы в положительном направлении (таким образом, что область межэлектродного пространства всегда находится слева),
– углы между отрезками, соединяющими середину k-го граничного элемента с начальной и конечной точкой m-го граничного элемента, соответственно, и внешней нормалью к m-му граничному элементу при прохождении границы в положительном направлении (таким образом, что область межэлектродного пространства всегда находится слева), ![]() – длина m-го граничного элемента. При этих обозначениях значения коэффициентов
– длина m-го граничного элемента. При этих обозначениях значения коэффициентов ![]() в (8) равны
в (8) равны
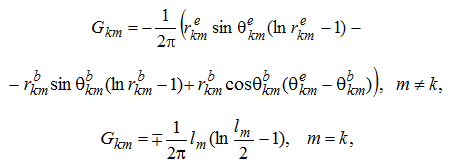 (10)
(10)
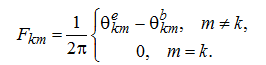 (11)
(11)
Знак «–» в (10) выбирается при проходе вдоль анода (против часовой стрелки), «+» выбирается при проходе вдоль катода (по часовой стрелке). При этом при интегрировании область всегда остается слева от контура интегрирования.
Как было указано выше, разобьем границы анода и катода на n1 и n2 прямолинейных граничных элементов соответственно. Координаты начальных и конечных точек этих элементов
![]()
при этом
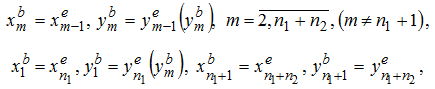 (12)
(12)
здесь элементы пронумерованы последовательно, сначала анод, затем катод, при этом сохраняется положительное направление обхода.
Подставляя в систему уравнений (8) граничные условия постоянства потенциала на аноде и катоде (4), получим систему линейных алгебраических уравнений для расчета нормальных производных ![]() на элементах
на элементах
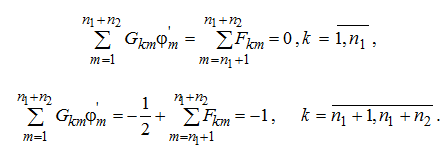 (13)
(13)
Матрица СЛАУ – заполненная, поэтому для решения задачи можно применить, например, метод Гаусса.
Полученные значения нормальных производных используются на следующих шагах алгоритма решения нестационарной задачи.
Способ изменения сетки заключается в первоначальном сдвиге угловых точек полигона (рис. 2). Затем положение этих точек видоизменяется так, чтобы длины элементов на аноде были равными. Для этого используется сплайн-интерполяция. При совершении шага очередная конфигурация ![]() интерполируется сплайнами (отдельно
интерполируется сплайнами (отдельно ![]() ,
, ![]() - длина участка границы, отсчитываемая от 0-й точки; изначально
- длина участка границы, отсчитываемая от 0-й точки; изначально ![]() ), задается положение узлов
), задается положение узлов ![]() , и решаются уравнения по определению параметра
, и решаются уравнения по определению параметра ![]() , при котором
, при котором ![]() . Координаты m-го узла с помощью сплайнов заменяются на
. Координаты m-го узла с помощью сплайнов заменяются на ![]() .
.
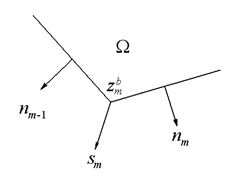
Рис. 2 – Сдвиг вершин полигона
Формулы шага по методу Эйлера аналогичны (5), (6).
На рис.3 и рис.4 приведены формы границ для различных значений круговой частоты w вращения ЭИ для τ=0, 2, 4, …, 20.
Видно, что для малых частот левая боковая граница паза приобретает существенную волнообразность формы, причем максимальная амплитуда волн наблюдается при ![]() . При
. При ![]() волнообразность практически исчезает.
волнообразность практически исчезает.
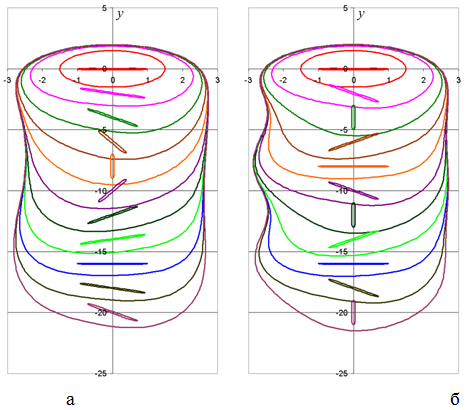
Рис. 3 – Формы обрабатываемой поверхности: а – ![]() ; б –
; б – ![]()
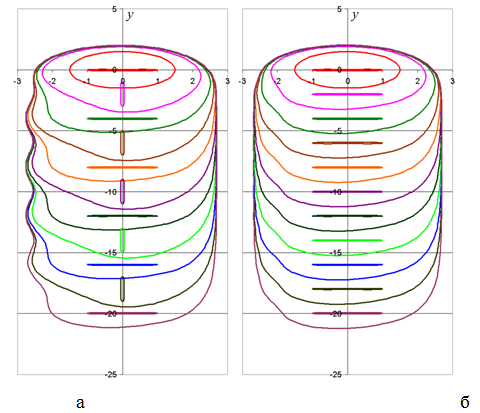
Рис. 4 – Формы обрабатываемой поверхности: а – ![]() ; б –
; б – ![]()
Явление образования волнообразной формы боковой части ОП можно объяснить следующим образом. При прохождении левой части зоны обработки кромка ЭИ движется вверх, поскольку ЭИ вращается по часовой стрелке, но центр ЭИ движется вниз. Тем самым, скорость движения кромки ЭИ относительно ОП уменьшается, и количество растворенного материала в левой части ОП увеличивается. При углах наклона ЭИ к оси x, близких к pn (n=1, 2, …), можно определить мгновенный центр вращения ЭИ Ct (рис. 5).
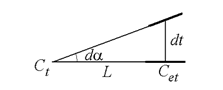
Рис. 5. –К определению положения центра вращения ЭИ
Расстояние L от Ct до центра ЭИ Cet определяется из уравнения
![]()
Отсюда при ![]() найдем
найдем ![]() .
.
Существует значение ω, при котором центр вращения находится на левой границе ОП. При ![]() величина L равна 2.55, что, судя по рис. 4,б приблизительно соответствует полуширине невозмущенного паза. Это же значение приближенно соответствует максимальной амплитуде волны, что подтверждается вычислительным экспериментом (рис. 3, 4). При увеличении w время прохождения центра вращения пропорционально уменьшается, но уменьшается и период волны на ОП, что компенсирует и то и другое. Поэтому наблюдаемый факт образования волнообразной формы левой границы максимальной амплитуды можно объяснить наиболее сильным «замиранием» кромки ЭИ вблизи левой части ОП при расположении мгновенного центра вращения ЭИ на границе ОП.
величина L равна 2.55, что, судя по рис. 4,б приблизительно соответствует полуширине невозмущенного паза. Это же значение приближенно соответствует максимальной амплитуде волны, что подтверждается вычислительным экспериментом (рис. 3, 4). При увеличении w время прохождения центра вращения пропорционально уменьшается, но уменьшается и период волны на ОП, что компенсирует и то и другое. Поэтому наблюдаемый факт образования волнообразной формы левой границы максимальной амплитуды можно объяснить наиболее сильным «замиранием» кромки ЭИ вблизи левой части ОП при расположении мгновенного центра вращения ЭИ на границе ОП.
Итак, был проведен вычислительный эксперимент с различными значениями угловой скорости w вращения ЭИ по часовой стрелке. Эксперимент показал, что левая граница прорезаемого паза при малых частотах приобретает волнообразную форму. При некотором значении w амплитуда волн имеет максимальное значение. Это было объяснено совпадением мгновенного центра вращения ЭИ, совершающего вращательное движение с одновременным поступательным движением его центра, с некоторой точкой на ОП. Это способствует наиболее длительному нахождению кромки ЭИ вблизи ОП и увеличению количества растворяемого материала.
Список литературы / References
- Волгин В. М. Моделирование электрохимической обработки проволочным электродом-инструментом / В. М. Волгин, До Ван Донг, А. Д. Давыдов // Изв. ТулГУ. Технические науки. – 2013. – Вып. 11. – С. 122–136.
- Volgin V. M. Modeling of wire electrochemical machining. / V. M. Volgin, V. D. Do, A. D. Davydov // Chem. Eng. Trans. – 2014. – V. 41. – P. 91-96.
- Житников В. П. Моделирование прецизионной нестационарной электрохимической обработки круглым и пластинчатым электрод-инструментом / В. П. Житников, Р. Р. Муксимова, А. А. Зарипов // Вестник УГАТУ. – 2015. – Т. 19 – №1 (67) – С. 92–99.
- Клоков В. В. Электрохимическое формообразование / В. В. Клоков // Изд-во Казань, ун-та, Казань. – 1984. – 80 с.
Список литературы на английском языке / References in English
- Volgin V. M. Modelirovanie electrohimicheskoi obrabotki provolochnim electrodom-instrumentom [Modeling of electrochemical machining with a wire electrode tool] / V. M. Volgin, V.D. Do, A. D. Davydov // Izv. TulGU. Technicheskie nauki [Collection of scientific works of Tulskiy University. Technical science]. – 2013. V. 11. P. 122–136. [in Russian]
- Volgin, V. M. Modeling of wire electrochemical machining. / V. M. Volgin, V. D. Do, A. D. Davydov // Chem. Eng. Trans. – 2014. – V. 41. P. 91-96. [in Eanglish]
- Zhitnikov V. P. Modelirovanie prezicionnoi nestacionarnoi electrohimicheskoi obrabotki krooglim i plastinchatim electrod-instrumentom [Modeling of Nonstationary electrochemical machining precision and circular plate of the electrode-tool] / V. P. Zhitnikov, R. R. Muksimova, A. A. Zaripov // Vestnik UGATU [USATU’s Gazette ]. – 2015. – V. 19 – №1 (67) – P. 92–99. [in Russian]
- Klokov V. V. Electrohimicheskoe formoobrazovanie [Electrochemical shaping] / V. V. Klokov // izdatelstvo Kazan, un-ta, Kazan [Publishing Kazan University]– 1984. – P. 80. [in Russian]
