КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ ВАЛОВОГО РЕГИОНАЛЬНОГО ПРОДУКТА ЯРОСЛАВСКОЙ ОБЛАСТИ

Чалик А.В.¹, Мудревский А.Ю.²

¹ORCID- 0000-0002-2502-5859 Аспирант,

²ORCID- 0000-0002-7334-3384 Кандидат экономических наук, доцент, заведующий кафедрой «Экономики и учетно-аналитической деятельности»

Международная академия бизнеса и новых технологий (МУБиНТ)

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ ВАЛОВОГО РЕГИОНАЛЬНОГО ПРОДУКТА ЯРОСЛАВСКОЙ ОБЛАСТИ

Аннотация

В статье произведен корреляционно-регрессионный анализ валового регионального продукта Ярославской области. Применены методы экстраполяции временного ряда. Найдены коэффициенты корреляции между исследуемыми переменными. Построена многофакторная модель, найдены коэффициенты регрессии, дана их экономическая интерпретация на примере области. Обоснованы направления роста ВРП путем развития взаимосвязанных и зависимых факторов объема строительно-монтажных работ, суммы оптовой и розничной торговли. Проверено качество построенной модели путем расчета среднеквадратичной ошибки. Предложены методы расчета, при разработке и реализации стратегии развития региона для федеральных и региональных органов управления.

Ключевые слова: Валовой региональный продукт, региональное управление, развитие, корреляционно-регрессионный анализ, экстраполяция временного ряда.

Chalick A.V.¹, Mudrevskiy A.Y.²

¹ORCID- 0000-0002-2502-5859 Postgraduate student,

²ORCID- 0000-0002-7334-3384 PhD in Economics, associate professor, head of the Department of «Economics and Accounting and Analytical Activities»

International Academy of Business and New Technologies (MUBiNT)

CORRELATION-REGRESSION ANALYSIS OF GROSS REGIONAL PRODUCT OF YAROSLAVL REGION

Abstract

The article presents correlation-regression analysis of the gross regional product of the Yaroslavl region. Methods of time series extrapolation are applied. Correlation coefficients between the considered variables are found. A multifactor model is constructed, coefficients of regression are discovered, and their economic interpretation is given on the example of the region. The directions of GRP growth are substantiated by means developing interrelated and dependent factors of the volume of construction, assembly works and the amount of wholesale and retail trade. The quality of the model is checked by calculating the root-mean-square error. Methods of calculation are proposed in the development and implementation of the regional development strategy for federal and regional government bodies.

Keywords: Gross regional product, regional management, development, correlation-regression analysis, extrapolation of time series.

 

Эффективность функционирования экономики страны во многом зависит от особенностей регионов. Их уровень развития определяется экономическим показателем - объемом валового регионального продукта (ВРП). Валовой региональный продукт, по своему экономическому содержанию, даёт наиболее полную картину о состоянии и развитии региона (области). Рост ВРП зависит от многих факторов и показателей, существующие между ними виды связей весьма разнообразны по своей классификации существуют, например, функциональные и стохастические связи.

Осуществление этапов распределения бюджета или выбора приоритетных направлений зачастую прерывается выявившимися препятствиями. Возникают ограничения в бюджетных средствах, проблемы организационно-мониторингового характера, которые не позволяют в должной мере использовать реально имеющийся потенциал социально-экономических систем для достижения максимальных результатов. В связи с чем встает вопрос о выборе приоритетных направлений развития региона. Проявляется необходимость в создании эффективного инструментария для региональных органов управления.

В данном исследовании используем совокупность методов экстраполяции временного ряда и корреляционно-регрессионного анализа для нахождения взаимосвязи, установление между ними причинно-следственной зависимости и влиянии факторов на ВРП в будущий момент времени. Расчеты выполнены на примере Ярославской области.

Временной ряд - это собранный в прошлый момент времени статистический материал о значениях исследуемых переменных изучаемого нами процесса. Данные были взяты за 2010-16 гг. из официальной статистической отчетности, ежегодных изданий Росстата «Регионы России. Социально-экономические показатели» [1], [2] (таблица 1). После чего статистические данные экстраполируются по 2018 год в соответствии со сложившимися тенденциями для дальнейшего анализа и планирования хозяйственно-экономической деятельности региона.

Таблица 1 – Экономические показатели Ярославской области

Ярославская область	валовой региональный продукт (млн. руб.)	объем строительно-монтажных работ (млн. руб.)	Оборот розничной и оптовой торговли (млн. руб.)
2010	239644	36823,7	299561
2011	286967,5	39816,9	354831
2012	327279,6	41496,8	386621
2013	362861,8	43495,3	422438
2014	388135,5	46132,7	491308
2015	431020,87	38632,1	543537
2016	468915,27	44065,04	582895,5

На рисунке 1 проиллюстрирован пример экстраполяции временного ряда. Метод экстраполирования это распространение выводов полученных из наблюдений на значение показателей в будущий момент времени.

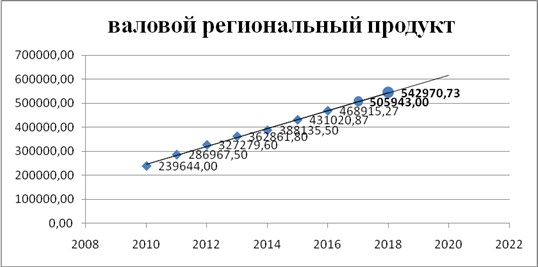
Рис. 1 - Экстраполяция временного ряда валового регионального продукта Ярославской области

Опираясь на полученные данные можно сделать прогноз, что ВРП по Ярославской области в 2017 г. предположительно составит 505943 млн. руб., а в 2018 г. 542970,73 млн. руб. Аналогичным образом спрогнозируем значения остальных переменных, объем строительно-монтажных работ и оборот розничной и оптовой торговли. По полученным результатам проведен корреляционно-регрессионный анализ.

В учебном пособии Харченко М.А. “Корреляционный анализ” дается определение: “Корреляционная зависимость – стохастическая зависимость между случайными величинами, при которой наблюдается функциональная зависимость между значениями одной величины и средними значениями другой величины” [3, С. 4]. Это наиболее подходящий вид анализа для использования его на примере регионов, поскольку регион можно и нужно рассматривать как хозяйственную деятельность.

Получи коэффициенты корреляции исходных данных. За результативный показатель возьмем валовой региональный продукт(Y) в качестве факторов используем объем строительно-монтажных работ(X₁) и сумму оборота розничной и оптовой торговли(X₂). Сначала проведем однофакторный анализ между Y: X₁; Y: X₂ и X₁: X₂ (таблица 2).

Таблица 2 – Расчеты корреляционного анализа

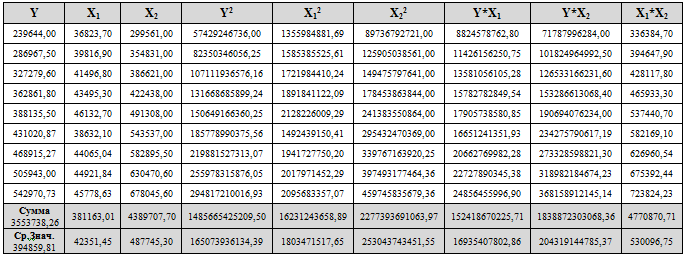
Продолжение таблицы 2

 

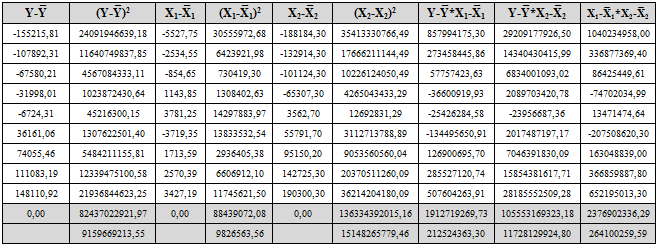
Перед тем, как искать коэффициент корреляции, необходимо установить есть ли между исследуемыми показателями корреляционный момент. Корреляционный момент, он же ковариация, характеризует наличие или же отсутствие связи между случайными величинами X₁, X₂ и Y. Формула для расчета ковариации:

Корреляционный момент во всех случаях отличен от нуля, следовательно, корреляционная связь существует между всеми переменными. Нормированное значение коэффициента ковариации называется коэффициентом корреляции [3, С. 11].

Для проверки наличия корреляции парной линейной связи используют линейный коэффициент парной корреляции, который является мерой пропорциональности степени зависимости явлений, показателем интенсивности линейной связи. Формула для нахождения коэффициентов:

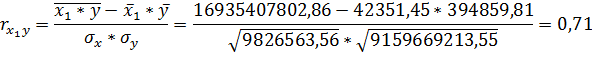
Коэффициент корреляции изменяется от -1 до +1. Если значение положительное то это свидетельствует о прямой связи, отрицательное значение - об обратной. Характеристики тесноты связи, отображенные в таблице 3, приведены из учебника “Военно-экономический анализ” под ред. С.Ф. Викулова [4, С. 197].

Таблица 3 – Количественные критерии оценки тесноты связи

Коэффициент парной корреляции между валовым региональным продуктом и объем строительно-монтажных работ (Y, X₁) является сильным видом связи; валовой региональный продукт и сумма оборота розничной и оптовой торговли (Y, X₂) является функциональной. Объем строительно-монтажных работ и сумма оборота розничной и оптовой торговли (X_1, X₂) являются факторами в данном исследовании и их уровень тесноты связи может быть причиной мультиколлинеарности. Мультиколлинеарность мешает правильному определению взаимосвязи. Если в регрессионную модель включить два или более линейно-зависимых факторов, то это усложнит процесс выделения наиболее существенных факторов, исказит смысл коэффициентов регрессии при их экономической интерпретации. В нашем случае, согласно полученным результатам, он не превысил допустимое значение 0,8.

Коэффициент корреляции проверяется путем нахождения t-критерия Стьюдента [4, С. 159]. Определим значение критерия t_расч. Затем проверим на нулевую гипотезу об отсутствии связи между факторами и ВРП с помощью t-критерия.

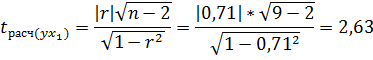
t_табл. =1.8331 с уровнем вероятности 0.90

Вычисленное по формуле значение  сравнивается с , который получают по таблице Стьюдента. В случае если , то связь считают существенной. Так как ,  и  то это означают, что связь является существенной для всех коэффициентов.

Регрессионный анализ является количественным методом определения вида математической функции в причинно-следственной зависимости между ВРП и факторами. Поэтому необходимо сделать прогноз результативного показателя, построением уравнения регрессии. Многофакторные модели обладают двумя достоинствами: простотой получения и достаточно ясной экономической интерпретацией. Линейное уравнение множественной регрессии имеет вид:

где х_i – факторные признаки;

 а_i – неизвестные параметры уравнения (коэффициенты регрессии).

Коэффициенты регрессии а_i показывают, насколько изменяется значение ВРП (Y) при увеличении i-го факторного признака (X_i) на единицу при фиксированном положении остальных факторов. Свободный член уравнения а₀ показывает усредненное влияние на результативный показатель всех неучтенных факторов. Для нашего исследования применим уравнения множественной регрессии с двумя факторами:

Для нахождения коэффициентов линейной двухфакторной модели необходимо решить систему уравнений с тремя неизвестными параметрами (a₀, a₁ и a₂) Для решения системы используют методы подстановок, сложения уравнений и др.:

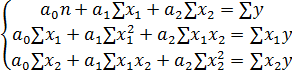
С полученными данными формула примет вид:

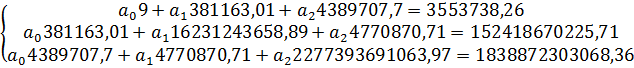
a₁  и a₂ являются коэффициентами регрессии, a₀ – свободным членом уравнения. Получим значение коэффициентов:

Уравнение линейной регрессии:

Дадим экономическую трактовку результатам построенной модели. Линейная регрессии выражает зависимость ВРП (Y) от объема строительно-монтажных работ (Х₁), суммы оптовой и розничной торговли (Х₂). Коэффициенты уравнения подтверждают наличие воздействия всех факторов на результативный показатель. В нашем случае валовой региональный продукт увеличивается в среднем на 1,542 млн. руб. При увеличении объема строительно-монтажных работ на 1 млн. руб. при неизменности показателя суммы оптовой и розничной торговли. Валовой региональный продукт увеличивается в среднем на 0,747 млн. руб. при увеличении суммы оптовой и розничной торговли на 1 млн. руб. при неизменности показателя объема строительно-монтажных работ.

Применим корреляционный анализ на многомерном случае. При изучении двумерной модели рассматривались только взаимосвязи парных коэффициентов корреляции, но этого недостаточно для многомерной модели. К. Пирсоном предложены множественные и частные коэффициенты, в которых отражено многообразие связей между переменными [4, С. 229].

Теснота связи между ВРП и всеми факторами измеряется при помощи коэффициента множественной корреляции:

Коэффициент множественной корреляции по определению является положительным и принимает значения в интервале между нулем и единицей. Если ВРП не связан с исследуемыми факторами линейной корреляционной зависимостью, то коэффициент примет значение близкое к 0. Коэффициент стремящийся к единице свидетельствует о сильной зависимости между признаками.. Полученный нами коэффициент составил 0,765, это говорит нам о сильной тесноте связи между факторами и ВРП.

Качество построенной модели проверяется, расчетом среднеквадратичной ошибки уравнения регрессии, предложенную Ф. И. Эджвортом[4, C. 206]:

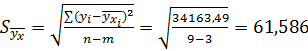
где m – число параметров в уравнении;

Относительная ошибка уравнения регрессии[4] - коэффициент вариации:

Достоинством коэффициента вариации является то, что он может служить мерой сравнения однородных по характеру величин, но имеющих существенную разницу в абсолютном значении. Если коэффициент вариации имеет значение менее 33 %, а в нашем случае так и есть, то построенным уравнением регрессии можно пользоваться для принятия управленческих решений.

Рассчитаем коэффициент детерминации [4,с.219], который показывает, какую часть вариации результативного признака объясняет построенная модель:

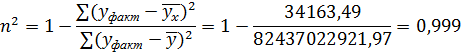
Долю дисперсии результативного признака Y, вызванную влиянием остальных не учтенных в модели факторов характеризует величина (1 – ). Следовательно факторы X₁ и X₂ объясняют, вариацию доходов на 99,9 %, а оставшийся 0,1 % является дисперсией результативного признака вызванного влиянием других, не учтенных в модели, факторов.

Соответственно, полученная нами регрессия и корреляция оказались адекватными. Результаты корреляции доказали существование связи между ВРП и объемом строительно-монтажных работ и суммой оборота розничной и оптовой торговли. Была построена модель регрессии, найдены коэффициенты регрессии и установлен уровень зависимости между переменными.

Использованные нами методы могут служить эффективным инструментарием для региональной власти при разработке и реализации стратегии развития региона, а так же для федеральных и региональных органов управления. Достаточная степень конкретности и достоверности показателей позволят: дать однозначную оценку фактическому состоянию региона; распределить бюджет, основываясь на результатах; обоснованно отстаивать точку зрения региона на федеральном уровне.

Список литературы / References

1. Официальный Интернет-сайт Росстата. [Электронный ресурс]. – URL: http://www.gks.ru. (дата обращения: 05.03.2017)
2. Территориальный орган Федеральной службы государственной статистики по Ярославской области [Электронный ресурс]. – URL: http://yar.gks.ru/wps/wcm/connect/rosstat_ts/yar/ru. (дата обращения 07.03.2017).
3. Харченко М.А. Корреляционный анализ: Учебное пособие для вузов. - Воронеж: Изд-во ВГУ, 2008. - 31 с.
4. Военно-экономический анализ: Учеб. / под общ. ред. С.Ф. Викулова. - Ярославль: ВФЭИ, 2010.

Список литературы на английском языке / References in English

1. Oficial'nyj Internet-sajt Rosstata [Official website of Rosstat]. [Electronic resource]. – URL http://www.gks.ru.. (accessed: 05.03.2017) [in Russian]
2. Territorial'nyj organ Federal'noj sluzhby gosudarstvennoj statistiki po Jaroslavskoj oblasti [Territorial body of the Federal State Statistics Service for the Yaroslavl Region]. [Electronic resource]. – URL: http://jar.gks.ru/shhps/shhcm/connect/rosstat_ts/jar/ru. (accessed 07.03.2017) [in Russian]
3. Harchenko M.A. Korreljacionnyj analiz [Correlation analysis]: Uchebnoe posobie dlja vuzov [A manual for universities]. - Voronezh: Izd VGU, 2008. - 31 p. [in Russian]
4. Voenno-jekonomicheskij analiz [Military-economic analysis]: Manual / ed. by S.F. Vikulova. - Jaroslavl': VFJeI, 2010. [in Russian]