ЭЛЕКТРОННОЕ СТРОЕНИЕ АТОМОВ ЩЕЛОЧНЫХ МЕТАЛЛОВ
Потапов А.А.
ORCID: 0000-0002-1006-9074, Доктор химических наук, профессор, Независимый исследователь
ЭЛЕКТРОННОЕ СТРОЕНИЕ АТОМОВ ЩЕЛОЧНЫХ МЕТАЛЛОВ
Аннотация
Целью настоящей статьи является обсуждение проблемы электронного строения атомов I группы таблицы Менделеева. Атомы представляют систему вложенных оболочек-квазисфер, наподобие русской матрешки. Дается анализ и обоснование механизмам формирования электронных оболочек атомов. Концептуальной основой теории электронного строения атомов выступает диполь-оболочечная модель. Для внешней оболочки атомов щелочных металлов предложена уточненная водородоподобная модель электронного строения. Внутренние электронные оболочки атомов представляют правильные геометрические фигуры разной симметрии, в том числе зеркально симметричной, тригональной, тетраэдрической, гексаэдрической и т.п. В рамках решения задачи Кеплера приводятся уравнения движения электронов на соответствующих оболочках. Получены формулы для описания и расчета основных параметров атомов. Определены эффективные радиусы атомов I группы. Обсуждается их поведение в группе. Характерным представляется то, что полученные радиусы приблизительно в два раза меньше имеющихся литературных данных; дается объяснение этому различию. Также определены основные параметры ряда внутренних оболочек атомов – константы экранирования, эксцентриситеты и большие полуоси эллиптических орбит.
Ключевые слова: атомы щелочных металлов, эффективные радиусы атомов, диполь-оболочечная модель.
Potapov A.A.
ORCID: 0000-0002-1006-9074, PhD in Chemistry, Professor, Independent researcher
ELECTRONIC STRUCTURE OF ALKALI METAL ATOMS
Abstract
The main goal of this paper is to consider the problem of the electronic structure of atoms of the 1st group of the periodic table. Atoms represent the system of nested shells-quasi-spheres, like a Russian Matryoshka. The analysis and justification are given on the formation mechanisms of electron shells of atoms. The conceptual basis of the theory of the electronic structure of atoms is a dipole-shell model. A refined hydrogen-like model of the electronic structure was proposed for the outer shell of alkali metal atoms. The internal electron shells of atoms represent regular geometric figures of different symmetry, including mirror symmetric, trigonal, tetrahedral, hexahedral, etc. Under the solution of the Kepler problem, the equations of motion of electrons on the corresponding shells are given. Formulas for description and calculation of the basic parameters of atoms are obtained. The effective radii of the atoms of the 1st group are determined. Their behavior in the group is considered as well. One of the characteristic features is that the radii obtained are approximately twice smaller in size compared to data from the literature; The explanation to this difference is also given in the paper. The basic parameters of a number of inner shells of atoms - screening constants, eccentricities and large semi-axes of elliptical orbits are also determined.
Keywords: atoms of alkali metals, effective atomic radii, dipole-shell model.
Атомы I группы таблицы Менделеева могут быть отнесены к классу водородоподобных структур. Они имеют по одному валентному электрону на внешней оболочке и квазисферический остов атома. В приближении недеформируемого остова атомы I группы в электрическом отношении подобны атому водорода. Из этого подобия следует, что к описанию щелочных металлов (атомам I группы) может быть привлечена классическая теория и соответствующая этой теории планетарная модель атома. Теперь в качестве притягивающего центра в атоме выступает положительный заряд qNе остова, где Nе ‒ число валентных электронов остова. Это означает, что многочастичную задачу атомов I группы можно свести к двухчастичной задаче, т.е. к задаче нахождения основных параметров движения вращающегося электрона в центральном поле заряда q остова атома [1].
Валентный электрон в поле заряда +q остова занимает одно из разрешенных вышестоящих уровней энергии (поскольку первая, K-оболочка занята). Следуя гипотезе квантования электронных оболочек, ближайший незанятый уровень водородоподобной структуры соответствует главному квантовому числу n =2, которому соответствует радиус, равный ![]() . Это означает, что в приближении водородоподобных атомов ожидаемая энергия связи
. Это означает, что в приближении водородоподобных атомов ожидаемая энергия связи ![]() атомов I группы должна быть равной
атомов I группы должна быть равной ![]() . При этом учтено то, что увеличение расстояния между ядром и электроном в 2 раза сопровождается уменьшением энергии взаимодействия между зарядами также в 2 раза. В этом заключается смысл коэффициента 1/n2 в данном соотношении. Величину
. При этом учтено то, что увеличение расстояния между ядром и электроном в 2 раза сопровождается уменьшением энергии взаимодействия между зарядами также в 2 раза. В этом заключается смысл коэффициента 1/n2 в данном соотношении. Величину ![]() надо понимать как определение энергии связи гипотетического атома, радиус круговой орбиты которого равен
надо понимать как определение энергии связи гипотетического атома, радиус круговой орбиты которого равен ![]() .
.
Измеряемой величиной, выступающей в качестве меры энергии связи ε1, является потенциал ионизации II. Его численные значения оказываются существенно отличными от гипотетической величины ![]() атомов I группы. Наблюдаемое различие
атомов I группы. Наблюдаемое различие ![]() связано с несовершенством принятой в исходном пункте модели водородоподобного атома. Единственной причиной данного несоответствия является заряд q остова атома, для которого ранее было принято приближение геометрической точки, имеющей единичный заряд +е [1].
связано с несовершенством принятой в исходном пункте модели водородоподобного атома. Единственной причиной данного несоответствия является заряд q остова атома, для которого ранее было принято приближение геометрической точки, имеющей единичный заряд +е [1].
В силу водородоподобной структуры атомов I группы уравнение движения валентного можно записать аналогично уравнению движения атома водорода с помощью потенциальной функции [1]
![]() (1)
(1)
где L – момент количества движения, q – эффективный заряд остова атома, r - радиус-вектор, ![]() , константа экранирования,
, константа экранирования, ![]() .
.
Существенным представляется то, что электронные орбиты атомов I группы являются круговыми, как и у атома водорода. Действительно, уравнение (1) с учетом константы экранирования можно представить в виде
![]() (2)
(2)
Функция ε(r) атомов I группы отличается от функции ![]() атома водорода только множителем σ/4. Отсюда следует важный вывод ‒ электронные орбиты атомов щелочных металлов являются круговыми (в отличие от ранее принятой модели эллиптических орбит [1]). Физический смысл круговой орбиты атомов I группы заключается в том, что изменение величины эффективного заряда q приводит к одновременному изменению орбитальной скорости v валентного электрона и радиуса r атома в соответствии с законом сохранения количества движения L=mvr. Так что для всех эффективных зарядов q кинетическая энергия остается равной половине потенциальной энергии атома.
атома водорода только множителем σ/4. Отсюда следует важный вывод ‒ электронные орбиты атомов щелочных металлов являются круговыми (в отличие от ранее принятой модели эллиптических орбит [1]). Физический смысл круговой орбиты атомов I группы заключается в том, что изменение величины эффективного заряда q приводит к одновременному изменению орбитальной скорости v валентного электрона и радиуса r атома в соответствии с законом сохранения количества движения L=mvr. Так что для всех эффективных зарядов q кинетическая энергия остается равной половине потенциальной энергии атома.
Решением уравнения (2) выступает энергия связи ε1 электрона
![]() (3)
(3)
где aI – радиус круговой орбиты, ![]() - боровский радиус.
- боровский радиус.
Здесь энергия связи ε1 определяется как результат притяжения валентного электрона к ядру в центральном поле заряда остова q = ![]() , находящегося на расстоянии
, находящегося на расстоянии ![]() .
.
Структурным параметром атомов I группы выступает радиус aI. Его можно определить непосредственно по уравнению (3) в приближении равенства энергии связи потенциалу ионизации II
![]() (4)
(4)
Константа экранирования определяется как отношение потенциала ионизации II атома к энергии гипотетического атома ![]() , у которого σ=1,
, у которого σ=1,
![]() (5)
(5)
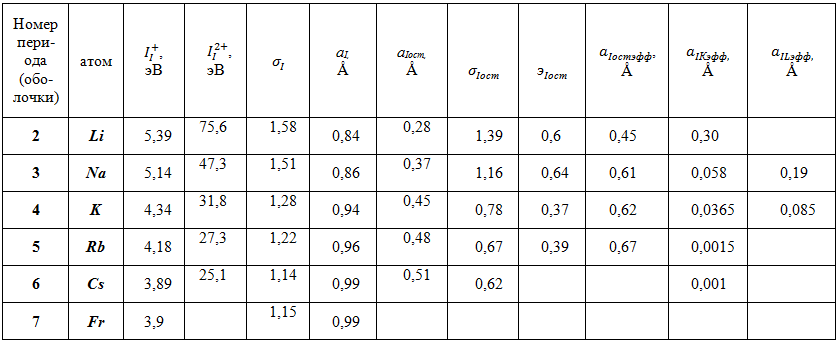
Рассчитанные по формулам (4) и (5) параметры атомов щелочных металлов приведены в таблице. В ряду атомов I группы константа экранирования закономерно снижается, отражая увеличение плотности эффективного заряда остова атомов по мере увеличения числа электронов в атомах. У атомов I группы константы экранирования имеют наибольшие численные значения по сравнению с другими атомами.
Радиусы атомов закономерно увеличиваются по мере увеличения числа внутренних оболочек атомов. Удивительно то, что при многократном весовом различии атомов их радиусы различаются незначительно, оставаясь в пределах 0,84Å у лития и 0,99Å у цезия. При этом радиусы атомов I группы ограничены удвоенным боровским радиусом ![]() = 1,06Å, которому соответствует радиус гипотетического атома на энергетическом уровне n=2 и константе экранирования σ=1. Численные значения радиусов приблизительно в два раза ниже литературных данных [2]. Различие между ними можно объяснить тем, что известные в литературе данные получены с помощью рентгеновских измерений, согласно которым определяется не радиус атомов, а половинное расстояние между ядрами близлежащих атомов в структуре исследуемого кристалла. При таком подходе к определению радиуса реальные размеры собственно атомов остаются не определенными. Что касается радиусов по (4), то их следует отнести к категории абсолютных, т.е. относящихся собственно к атомам. Численные величины радиусов атомов щелочных металлов получены впервые.
= 1,06Å, которому соответствует радиус гипотетического атома на энергетическом уровне n=2 и константе экранирования σ=1. Численные значения радиусов приблизительно в два раза ниже литературных данных [2]. Различие между ними можно объяснить тем, что известные в литературе данные получены с помощью рентгеновских измерений, согласно которым определяется не радиус атомов, а половинное расстояние между ядрами близлежащих атомов в структуре исследуемого кристалла. При таком подходе к определению радиуса реальные размеры собственно атомов остаются не определенными. Что касается радиусов по (4), то их следует отнести к категории абсолютных, т.е. относящихся собственно к атомам. Численные величины радиусов атомов щелочных металлов получены впервые.
Структура внутренних оболочек атомов I-й группы формируется по общим для всех атомов таблицы Менделеева принципам в соответствии с диполь-оболочечной моделью [1]. В рамках данной модели стало возможным рассчитать размеры внутренних оболочек. При этом общий подход к определению параметров атомов остается прежним, основанным на данных измерения потенциалов ионизации с учетом их электронных конфигураций.
Наиболее простое строение у атома лития, имеющего одну внутреннюю оболочку (К-оболочку). Она образована двумя эллиптическими электронными орбитами с общим фокусом на ядре. Уравнение движения электронов можно представить с помощью потенциальной функции [1]
![]() (6)
(6)
где первое слагаемое представляет кинетическую энергию вращения электронов по эллиптическим орбитам, второе слагаемое – энергия притяжения электронов в поле заряда ядра 3е![]() , третье слагаемое – энергия взаимного отталкивания электронов с учетом эффекта экранирования.
, третье слагаемое – энергия взаимного отталкивания электронов с учетом эффекта экранирования.
Решением уравнения движения каждого из электронов остова-катиона атома выступает энергия связи в соответствии с (6)
![]() (7)
(7)
где ![]() – большая полуось эллиптической орбиты каждого электрона. Здесь первое слагаемое представляет энергию притяжения каждого валентного электрона на эллиптической орбите в центральном поле заряда +3е
– большая полуось эллиптической орбиты каждого электрона. Здесь первое слагаемое представляет энергию притяжения каждого валентного электрона на эллиптической орбите в центральном поле заряда +3е![]() остова с учетом энергии центробежного отталкивая электрона (коэффициент 1/2), второе слагаемое – энергия взаимного отталкивания валентных электронов на расстоянии удвоенного радиуса
остова с учетом энергии центробежного отталкивая электрона (коэффициент 1/2), второе слагаемое – энергия взаимного отталкивания валентных электронов на расстоянии удвоенного радиуса ![]()
В приближении ![]() на основании уравнения (7) можно рассчитать длину большой полуоси лития
на основании уравнения (7) можно рассчитать длину большой полуоси лития
![]() (8)
(8)
Входящую в данное уравнение константу экранирования можно рассчитать по формуле ![]() в соответствии с (5), где
в соответствии с (5), где ![]() энергия связи круговой орбиты электронов остова гипотетического катиона-остова, образованного парой эллиптических орбит с общим фокусом на ядре.
энергия связи круговой орбиты электронов остова гипотетического катиона-остова, образованного парой эллиптических орбит с общим фокусом на ядре.
Для определения величины ![]() нужно решить уравнение движения электронов на своих эллиптических орбитах в приближении σ=1, так что
нужно решить уравнение движения электронов на своих эллиптических орбитах в приближении σ=1, так что
![]() (9)
(9)
Здесь первое слагаемое представляет кинетическую энергию электронов, второе слагаемое – энергия притяжения электронов в поле заряда +3е остова-катиона с учетом энергии центробежного отталкивая электрона (коэффициент 1/2), третье слагаемое – энергия межэлектронного отталкивания на удвоенном расстоянии 2r.
Его решением является энергия связи электронов остова, представляющая минимум потенциальной энергии (9)
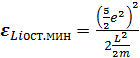 (10)
(10)
Эта энергия соответствует энергии гипотетической круговой орбиты остова, так что ![]() . Расчет по (10) дает
. Расчет по (10) дает ![]() = 84,4эВ. Принимая табличное значение потенциала
= 84,4эВ. Принимая табличное значение потенциала ![]() = 75,6эВ, получаем
= 75,6эВ, получаем ![]() = 0,89 и соответственно подстановка этой величины в (8) дает для большой полуоси эллиптической орбиты остова
= 0,89 и соответственно подстановка этой величины в (8) дает для большой полуоси эллиптической орбиты остова ![]() = 0,23Å.
= 0,23Å.
Учитывая динамический характер электронов, обусловленный вращением электронов с огромными скоростями, атом следует рассматривать как сферу с эффективным радиусом, определяемым максимальным расстоянием электрона от ядра, т.е. расстоянием в апогее rA,
![]()
Входящий в это уравнение эксцентриситет э эллиптической орбиты можно определить с помощью величины ![]() на основании известной формулы [3]
на основании известной формулы [3]
![]()
из которой следует э = 0,33, так что для лития получаем эффективный радиус равен ![]() = 0,23Å·1,33 = 0,30Å.
= 0,23Å·1,33 = 0,30Å.
У остальных атомов щелочных металлов в качестве остова выступают 6-и электронные оболочки, образованные эллиптическими орбитами с общим для них фокусом на ядре. Уравнение движения электронов остова принимает следующий вид
![]() (13)
(13)
Здесь первое слагаемое представляет кинетическую энергию электронов, второе слагаемое – энергия притяжения электронов в поле заряда +7е![]() остова-катиона с учетом энергии центробежного отталкивая электрона (коэффициент 1/2), третье слагаемое – энергия отталкивания выделенного электрона от остальных пяти валентных электронов на удвоенном расстоянии 2r.
остова-катиона с учетом энергии центробежного отталкивая электрона (коэффициент 1/2), третье слагаемое – энергия отталкивания выделенного электрона от остальных пяти валентных электронов на удвоенном расстоянии 2r.
Его решением является энергия связи электронов остова
![]() (14)
(14)
где ![]() – большая полуось эллиптической орбиты остова.
– большая полуось эллиптической орбиты остова.
Данное уравнение в приближении ![]() является основой для определения длины большой полуоси
является основой для определения длины большой полуоси
![]() (15)
(15)
Входящая в (14) константа экранирования рассчитывается по формуле (5). Рассчитанные величины ![]() приведены в таблице.
приведены в таблице.
Чтобы найти радиус остова атомов необходимо учесть фактор эллиптичности, т.е. определить эксцентриситеты э эллиптических орбит. Его можно найти с помощью формулы, аналогичной (12) [3]
![]()
где ![]() - энергия круговой орбиты остова, равная минимуму
- энергия круговой орбиты остова, равная минимуму ![]() потенциальной энергии (13), которую можно найти аналогично (10), так что
потенциальной энергии (13), которую можно найти аналогично (10), так что ![]() . Эта энергия соответствует энергии гипотетической круговой орбиты остова, так что
. Эта энергия соответствует энергии гипотетической круговой орбиты остова, так что ![]() . Учитывая динамический характер электронов, остов атома можно представить как сферу с эффективным радиусом, определяемым как максимальное расстояние электрона от ядра, т.е. расстояние в апогее эллиптической орбиты. Радиусы остовов атомов определяются аналогично (11),
. Учитывая динамический характер электронов, остов атома можно представить как сферу с эффективным радиусом, определяемым как максимальное расстояние электрона от ядра, т.е. расстояние в апогее эллиптической орбиты. Радиусы остовов атомов определяются аналогично (11), ![]() , где э ‒ эксцентриситет эллиптических электронных орбит, который находится с помощью (16). Рассчитанные величины
, где э ‒ эксцентриситет эллиптических электронных орбит, который находится с помощью (16). Рассчитанные величины ![]() и приведены в таблице.
и приведены в таблице.
Наличие данных по эксцентриситетам позволяет рассчитать малую полуось остова атома [3] ![]() .
.
Данные по высшим степеням потенциалов ионизации также позволяют определить параметры некоторых внутренних оболочек атомов.
К-оболочки образованы двухэлектронными эллиптическими орбитами с общим фокусом на ядре. Для них уравнение движения электронов принимает следующий вид
![]() (17)
(17)
где ZI - порядковый номер элементов, соответствующих атомам I-группы, т.е. ZI = 1, 3, 11, 19, 37, 55. Здесь первое слагаемое представляет кинетическую энергию электронов, второе слагаемое – энергия притяжения электронов в поле заряда ![]() остова-катиона с учетом энергии центробежного отталкивая электрона (коэффициент 1/2), третье слагаемое – энергия взаимного отталкивания электронов на удвоенном расстоянии 2r. Его решением по аналогии с (7) является энергия связи
остова-катиона с учетом энергии центробежного отталкивая электрона (коэффициент 1/2), третье слагаемое – энергия взаимного отталкивания электронов на удвоенном расстоянии 2r. Его решением по аналогии с (7) является энергия связи
![]() (18)
(18)
Таблица 1 – Экспериментальные и рассчитанные параметры атомов I группы таблицы Менделеева
На основании (18) в приближении![]()
У атома лития К-оболочка соответствует его остову. Для него было получено ![]() .
.
По приведенной выше методике для К-оболочек получены следующие параметры: натрий ‒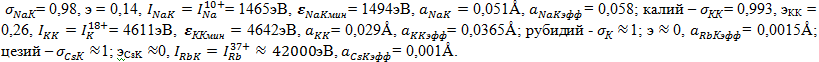
Для L-оболочек исходным для расчетов является уравнение движения электронов, наподобие (17),
![]() (20)
(20)
где ![]() – большая полуось эллиптических орбит L-оболочек.
– большая полуось эллиптических орбит L-оболочек.
На основании (21) в приближении ![]() можно найти большие полуоси эллиптических орбит L-оболочек
можно найти большие полуоси эллиптических орбит L-оболочек
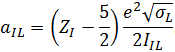
В результате расчетов параметров L-оболочек получены следующие параметры: натрий
Таким же образом удалось рассчитать параметры М-оболочки атома калия:
![]()
Данные по потенциалам ионизации для расчета параметров атомов взяты из справочников [4], [5].
На основании полученных данных в качестве иллюстрации на рисунке схематически представлены атомы щелочных металлов в относительном масштабе. Внешние и внутренние оболочки представлены в виде квазисфер. В центре оболочек черными кружками показаны ядра атомов. Видно, что, несмотря на увеличение числа внутренних оболочек, размеры атомов в ряду щелочных металлов изменяются незначительно.
Выводы

Рис. 1
В рамках диполь-оболочечной модели дано динамическое описание атомов I группы таблицы Менделеева. Получены формулы для расчета основных параметров атомов, по которым определены эффективные радиусы, константы экранирования, большие полуоси эллиптических орбит ряда внутренних оболочек и их эксцентриситеты.
Список литературы / References
- Потапов А.А. Ренессанс классического атома / А.А. Потапов. ‒ М.: Издательский Дом “Наука”. LAP LAMBERT Academic publishing. 2011. ‒444 с.
- БацановС.С. Структурная химия. Факты и зависимости / C. С. Бацанов. М.: Диалог-МГУ, 2000. ‒ 292 с.
- Киттель Ч., Найт В., Рудерман М. Механика / Ч. Киттель, В. Найт, М. Рудерман ‒ М.: Наука. ‒ 448 с.
- Физические величины: Справочник . – М.:Энергоатомиздат, 1991. – 1232 с.
- Яценко А.С. Оптические спектры Н- и Не-подобных ионов / А.С. Яценко – Новосибирск: Наука, – 216 с.
Список литературы на английском языке / References in English
- Potapov A.A. Renessans klassicheskogo atoma [Renaissance of the classical atom / A.A. Potapov. ‒ М.: Publishing house “Nauka”, LAPLAMBERT Academic publishing. 2011. – 444 p. [in Russian]
- Batsanov S.S. Structural chemistry book of facts [Structural chemistry book of facts] / S.S. Batsanov. ‒ M.: Dialog-MGU. 292 p. [in Russian]
- Kittel Ch., Knight W., Ruderman M. Mechanics [Mechanics] / Ch.Kittel, W.Knight, R M.uderman. М: Nauka, 1983. ‒ 448 p. [in Russian]
- Physical quantities: Reference book [Physical quantities: Reference book]. – M.:Energoatomizdat, 1991. – 1232 p. [in Russian]
- Yatsenko A. S. Optical spectra of H- and He-like ions [Optical spectra of H- and He-like ions] / A. S. Yatsenko. – Novosibirsk: Nauka, 2003. – 216 p. [in Russian]