ВЛИЯНИЕ КРИВИЗНЫ ПОВЕРХНОСТИ МАТЕРИАЛА НА РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТЕЙ ПРИ РЕНТГЕНОДИФРАКЦИОННОМ АНАЛИЗЕ
ВЛИЯНИЕ КРИВИЗНЫ ПОВЕРХНОСТИ МАТЕРИАЛА НА РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТЕЙ ПРИ РЕНТГЕНОДИФРАКЦИОННОМ АНАЛИЗЕ
Научная статья
Жигачев А.О.
Студент, Научно-образовательный центр “Нанотехнологии и наноматериалы” при ТГУ имени Г.Р. Державина
Аннотация
В работе рассмотрены результаты экспериментального изучения влияния кривизны поверхности поликристаллического материала, исследуемого методами рентгенодифракционного анализа, на профиль отдельного рефлекса и на общее распределение интенсивностей дифракционных пиков. Эффект, описанный в работе, может быть полезен для усовершенствования методики рентгенофазного анализа с целью более точного определения количественного соотношения фаз.
Ключеые слова: рентгеновская дифракция, систематические погрешности.
Keywords: XRD, systematic aberrations.
Рентгенодифракционный анализ является одним из наиболее распространенных методов анализа строения кристаллического вещества в большинстве современных лабораторий. С использованием методов рентгенофазного анализа возможно определение содержания различных фаз в исследуемом материале с точностью до одного весового процента. С применением рентгеноструктурного анализа и, в частности, метода Ритвельда возможно определение не только пространственной группы кристалла, но и расположения атомов внутри элементарной ячейки и множества других параметров. Однако проведение точного анализа состава и структуры материала предъявляет существенные требование к качеству подготовки образца, что, при современном развитии методов интерпретации получаемых экспериментальных данных, оказывается лимитирующим фактором при рентгенодифракционном анализе.
Из литературных данных [1, 2] известно, что наибольшее влияние на интенсивность отдельных пиков на дифрактограмме оказывает преимущественная ориентация кристаллитов, которая является, по сути, случайной ошибкой, то есть на настоящий момент предварительное определение ориентации кристаллитов с целью улучшения качества получаемых дифрактограмм затруднено и практически не применяется. Данный вид погрешности обусловлен особенностями исследуемого вещества, поэтому более практичным оказывается учет влияния преимущественной ориентации постфактум на полученной дифрактограмме.
Долгое время наиболее существенной систематической аберрацией при рентгенодифракционных исследованиях была погрешность, вызванная аксиальной расходимостью пучка, то есть расходимость вдоль линии параллельной оси гониометра. Эта аберрация вызывает смещения центра тяжести пика в область меньших углов, пик становится сильно ассиметричным и плохо описывается функциями PseudoVoigt и Split PseudoVoigt. Однако в настоящее время удалось значительно уменьшить влияние этого рода погрешностей путем применения щелей Соллера в дифрактометрах и метода фундаментальных параметров [3] при анализе дифракционных данных.
Таким образом, в современных дифрактометрах основную часть систематических аберраций составляют погрешности вызванные смещением образца в направлении, перпендикулярном к фокусирующей окружности гониометра и погрешности, вызванные особенностями подготовки поверхности. Большая часть этих погрешностей довольно подробно изучена и методы, позволяющие их учесть, широко применяются при анализе дифрактограмм.
Однако проблема влияния кривизны поверхности на геометрию дифракционных пиков относительно слабо изучена – рассчитаны лишь коррекции для цилиндрического образца в геометрии Дебая-Шеррера [4], хотя и представляет некоторую научную и практическую ценность. При анализе поликристаллических материалов зачастую возникают ситуацию, в которых приходится производить изучения образца сложной формы, например, в при работе с веществами, которые испытывают фазовые превращения при возникновении механических напряжения. Фазовый состав таких веществ после помола или шлифовки может значительно измениться, что приведет к невозможности определить состав исходного вещества.
Понимание влияния кривизны поверхности на результаты рентгенодифракционных исследований может оказаться полезным, так как любую поверхность сложной формы можно представить в виде некоторой комбинации искажений поверхности, каждое из которых имеет более простую форму. В данной работе произведено экспериментальное изучение влияния кривизны цилиндрической поверхности на геометрию пиков.
В качестве исследуемого образца мы использовали свинцовую деталь следующей формы: одна поверхность образца была плоской, вторая имела цилиндрическую форму с радиусом кривизны поверхности 12 мм. Образец изготавливался из свинца методом плавления в предварительно подготовленной керамической форме с последующей многостадийной шлифовкой. Исследование проводилось на рентгеновском дифрактометре Bruker AXS D2 Phaser с использованием отражательной геометрии Брегга-Брентано. Ниже приведены основные инструментальные параметры проведенных нами измерений.
1) Радиус гониометра, мм 141;
2) Угловая апертура щели расходимости, град. 0,24;
3) Первичная и вторичная щели Соллера, град. 2,5;
4) Используемый шаг измерения, град. 0,02;
5) Длина волны излучения, Å 1,54;
6) Детектор излучения Линейный PSD.
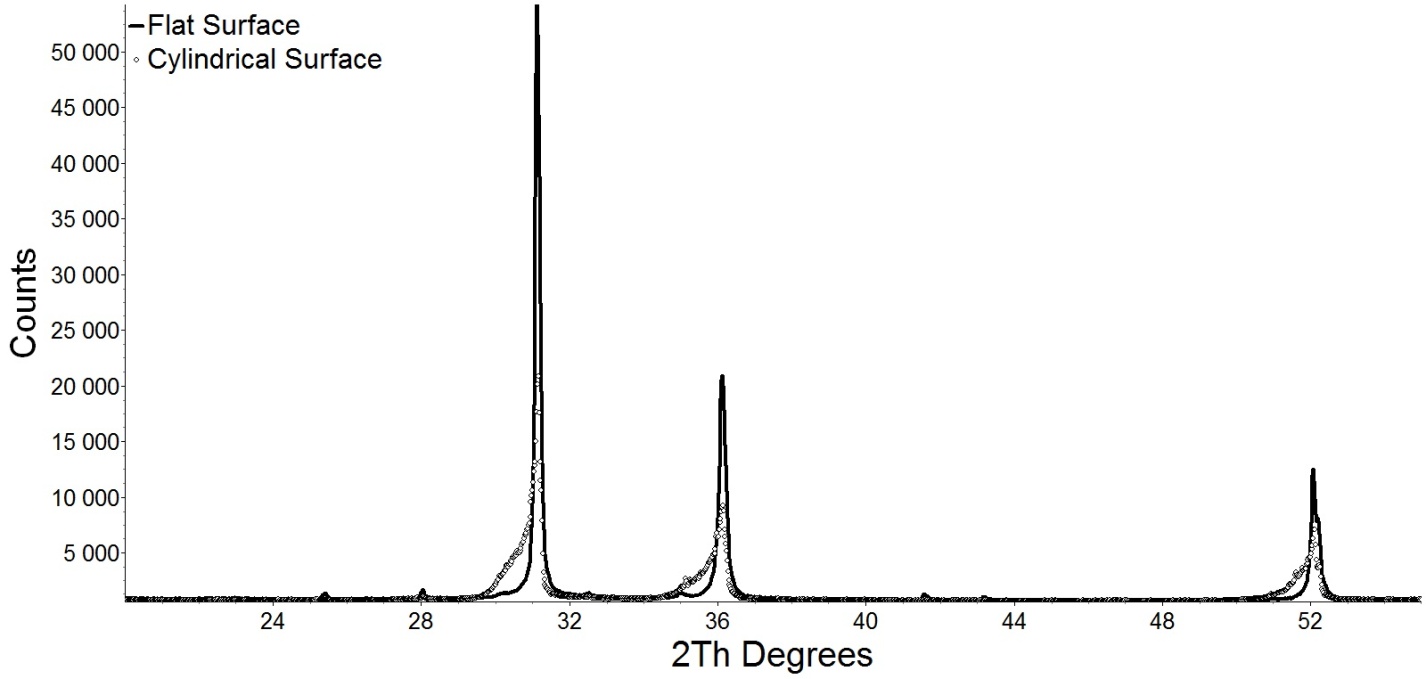
Снятие дифрактограммы производилось в угловом диапазоне 20-55 градусов 2θ, в котором расположены три рефлекса Pb, соответствующие кристаллографическим семействам плоскостей: {1 1 1}, {0 0 2}, {0 2 2}. Малое количество рефлексов, обусловленное высокой симметрией кристаллической решетки свинца (пространственная группа – 225) позволило изучить изменение геометрии отдельных пиков без влияния соседних рефлексов. Ниже, на рис. 1. приведены дифрактограммы полученные для плоской поверхности (сплошная линия) и для цилиндрической (полые кружки).
Рис. 1.Обзорная дифрактограмма
На рис. 1 хорошо видно, что при снятии дифрактограммы с плоской поверхности интенсивность пиков выше, чем при дифракции на цилиндрической поверхности. Это можно объяснить тем, что происходит перераспределение интегральных интенсивностей пиков с образованием сильно ассиметричного пика, центр тяжести которого смещен в сторону меньших углов 2θ. Можно заметить, что соотношение интенсивностей пиков увеличивается при увеличении угла сканирования. Полученные соотношения интенсивностей малых и больших пиков равны для наблюдаемых рефлексов, соответственно: 0,39; 0,46; 0,47.
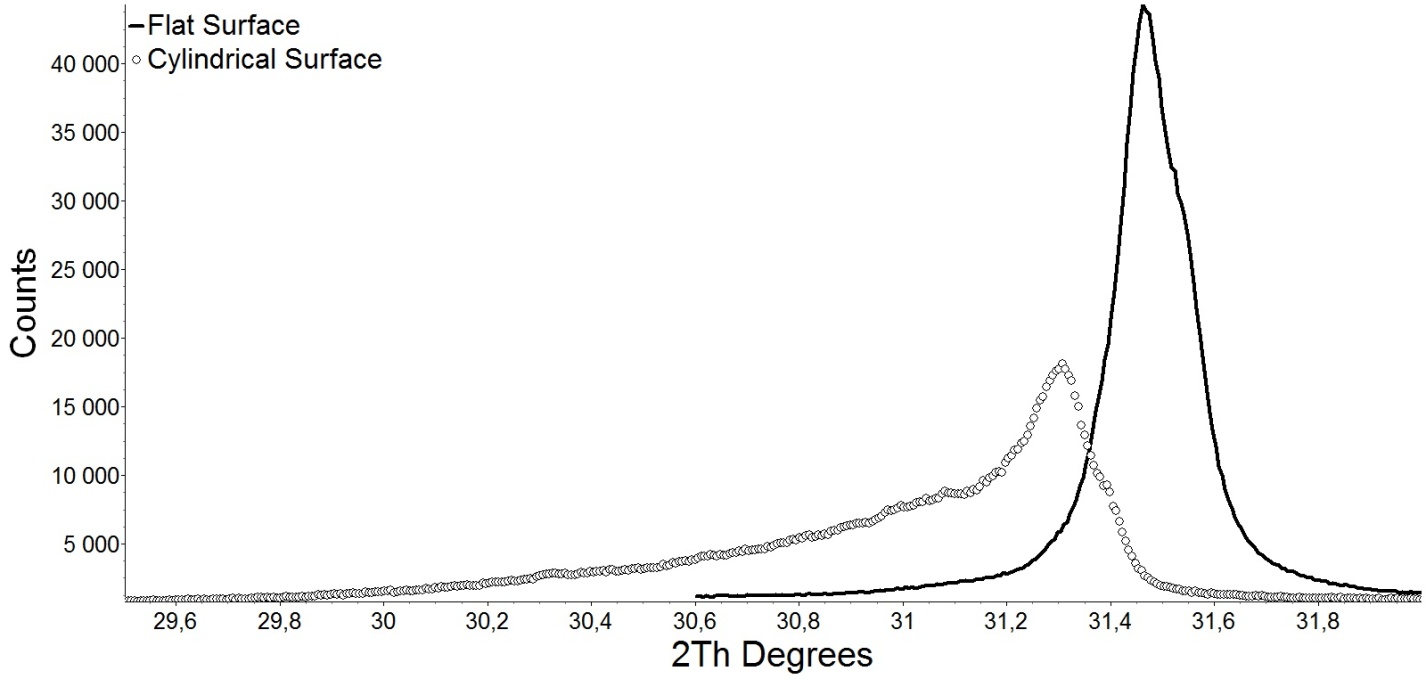
Также нами была произведена более подробная съемка геометрии рефлекса, соответствующего углу 2θ » 31°. В данном случае угловой шаг съемки составил 0,006° 2θ. Ниже, на рис. 2, показана типичная полученная нами картина для плоской (сплошная линия) и цилиндрической (полые кружки) поверхностей.
Рис.2. Подробная дифрактограмма отдельного рефлекса
На рис. 2. хорошо видно, что происходит “размазывание” интенсивности рефлекса в сторону меньших углов. Левая часть ассиметричного пика представляется гладкой функцией, на которой расположены низкоинтенсивные выбросы, обусловленные наличием шероховатости и, возможно, макроскопических дефектов на поверхности образца. Смещение максимумов двух рефлексов, представленных на рис.2 может быть объяснено двумя способами:
1) неточность установки плоскости, касательной к исследуемой цилиндрической поверхности, в измерительную кювету
2) Систематическое смещение пика, вызванное кривизной поверхности
Описание геометрии сложного ассиметричного пика представляет собой интересную теоретическую задачу. Решение ее представляется возможным при расширении фундаментальных параметров на случай кривизны поверхности в геометрии на отражение, а также путем подбора эмпирических функций и применением операции свертки к ассиметричной оконной функции и семейству PseudoVoigt, что рассмотрено в работах [5-7].
Таким образом, проведенная работа может оказаться полезной для экспериментального и теоретического изучения влияния поверхности на качество и результаты рентгенодифракционных исследования, а также для разработки методов учета этих погрешностей, с целью увеличения точности получаемых данных и для уменьшения требований к подготовке образцов.
Список литературы / References
1) Introduction to X-ray Powder Diffractometry. Ron Jenkins, Robert L. Snyder. John Wiley & Sons Ltd. (1996);
2) X-Ray Diffraction by Pollycrystaline Materials. René Guinebretière. ISTE Ltd. (2007);
3) Fundamental Parameters Line Profile Fitting in Laboratory Diffractometers, J. Res. Natl. Inst. Stand. Technol. 109, 1-25 (2004);
4) Analytical Expressions for the Transmission Factor and Peak Shift in Absorbing Cylindrical Specimen. J. Appl. Cryst. 31, 47-51 (1998);
5) Flat-specimen effect as a convolution in powder diffractometry with Bragg-Brentano geometry. J. Appl. Cryst. 32, 634-640 (1999);
6) An efficient method for calculating asymmetric diffraction peak profiles. Rev. Sci. Instrum. 69, 3837 (1998);
7) Effect of sample transparency in powder diffractometry with Bragg-Brentano geometry as a convolution. J. Appl. Cryst. (1999). 32, 982-991.