ЭНТРОПИЙНАЯ ЭФФЕКТИВНОСТЬ ТЕПЛОПОТРЕБЛЯЮЩИХ ОБЪЕКТОВ
ЭНТРОПИЙНАЯ ЭФФЕКТИВНОСТЬ ТЕПЛОПОТРЕБЛЯЮЩИХ ОБЪЕКТОВ
Научная статья
Требунских С.А.
Канд. техн. наук, кафедра тепловых электрических станций, Забайкальский государственный университет – ЗабГУ.
Аннотация
В статье рассмотрен метод определения энтропийной эффективности на основе закономерностей линейной неравновесной термодинамики, позволяющий численно рассчитать относительную степень совершенства различных теплопотребляющих объектов.
Ключевые слова: термодинамика, энтропия, эффективность.
Key words: thermodynamics, entropy, efficiency.
Термодинамика неравновесных процессов широко применяется преимущественно при изучении процессов с химическими превращениями веществ, существенные результаты получены и в направлении информационных процессов. Центральными понятиями термодинамики неравновесных процессов являются энтропия и производство энтропии. Теория информации также развивается с применением термина «энтропия», поскольку отмечено совпадение формул для разности статистической энтропии и количества информации. В рамках теории информации появился термин «негэнтропия», параметр, противоположный энтропии. Вместе с тем в ряде основополагающих работ негэнтропия вообще не рассматривается [1, 3], а энтропия не получает словесного определения, ограничиваясь математической записью. Чаще всего встречается утверждение, что энтропия есть мера беспорядка системы. Однако данное утверждение применимо к так называемой информационной энтропии, которую, согласно [4], отождествлять с энтропией термодинамической не следует.
Прикладные теплоэнергетические задачи в подавляющем большинстве случаев решаются с применением закономерностей классической равновесной термодинамики. Учитывая значительные достижения в применении методов неравновесной термодинамики в различных областях науки и техники, возникает потребность использовать эти методы и при решении теплоэнергетических задач. Особенно актуально применение данных понятий при разработке критериев эффективности различных тепловых процессов.
Фундаментальный смысл второго начала термодинамики заключается в том, что самопроизвольный поток энергии в термодинамической системе направлен от большей плотности энергии к меньшей, к примеру, тепловой поток движется от большей температуры к меньшей. Поскольку любой подобный поток необратим, должна существовать некоторая монотонная функция состояния, всегда либо возрастающая, либо убывающая. Эта функция и есть энтропия.
Мощность теплового потока через разделяющую две среды стенку описывается общепринятым уравнением:
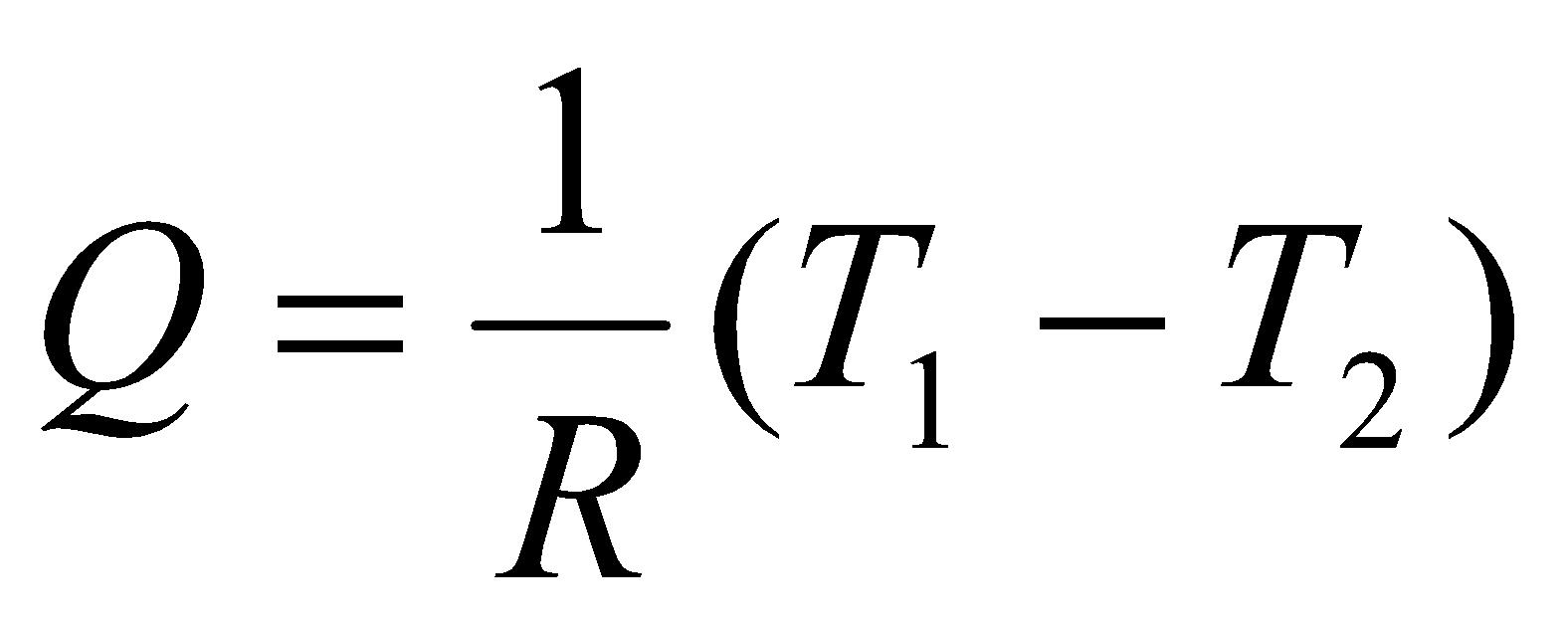
 ,
,
где R – средний коэффициент полного термического сопротивления среды, учитывающий коэффициенты теплопроводности и теплоотдачи, толщину среды (стенки или стенок) и площадь теплообмена, через которую протекает данный тепловой поток, и имеющий размерность оК/Вт. Если привести размерности термического сопротивления и температур к энергетической, умножая на постоянную Больцмана, то получим [R]=Дж/Вт.
Центральным понятием неравновесной термодинамики является производство энтропии. Общепринятая формула производства энтропии потоком теплоты через среду, имеющую ненулевое термическое сопротивление, имеет вид
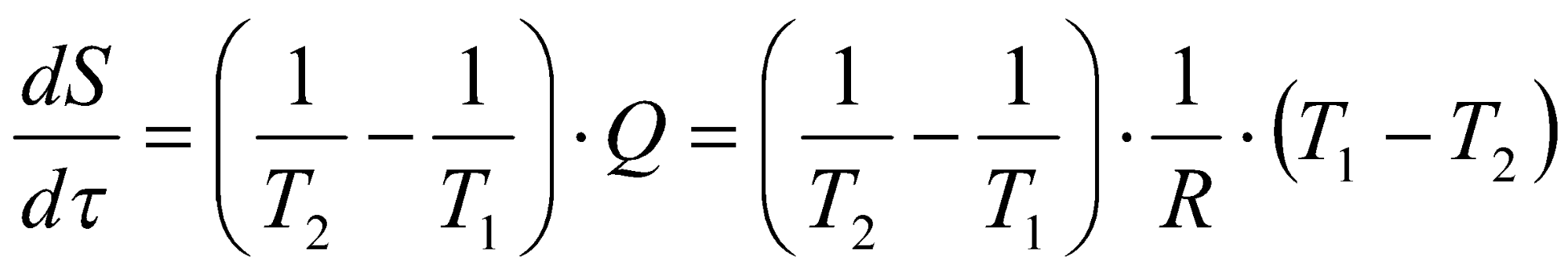
 .
.
Перепишем уравнение производства энтропии тепловым потоком введя параметр 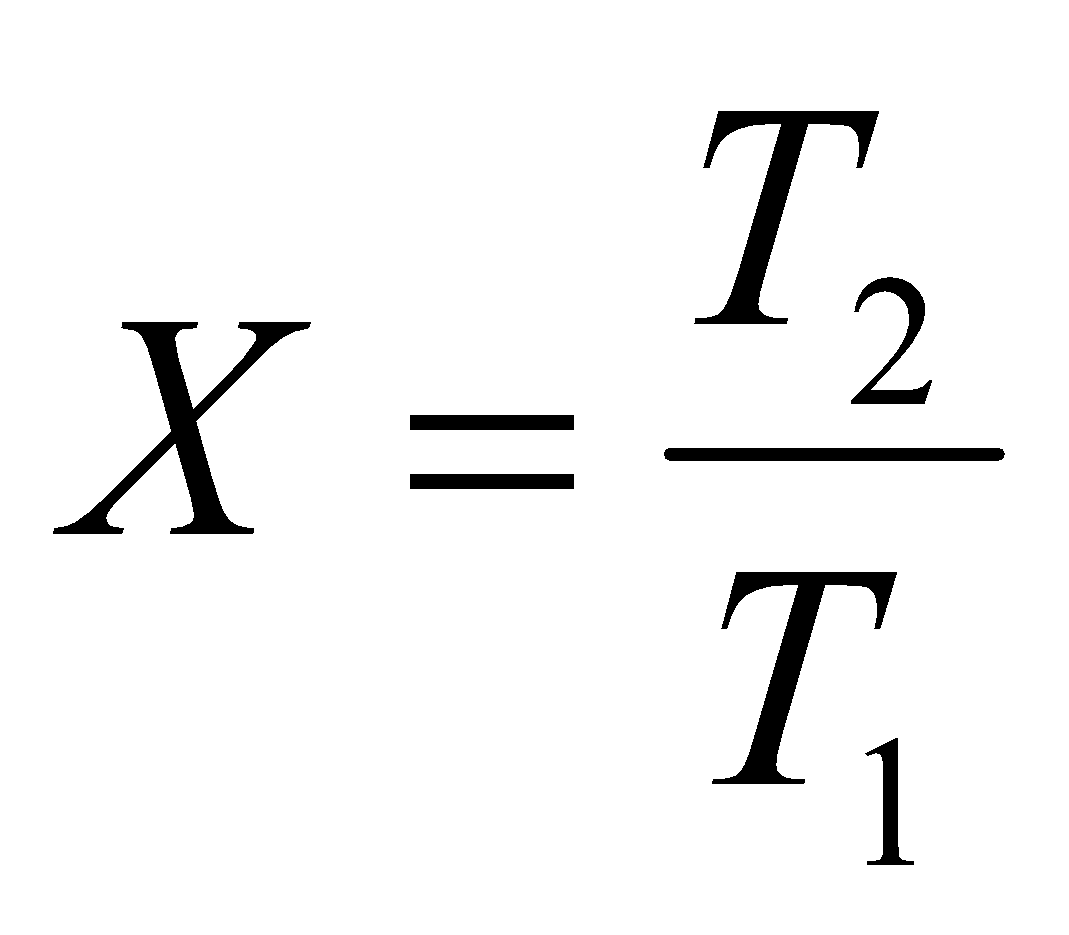
 :
:
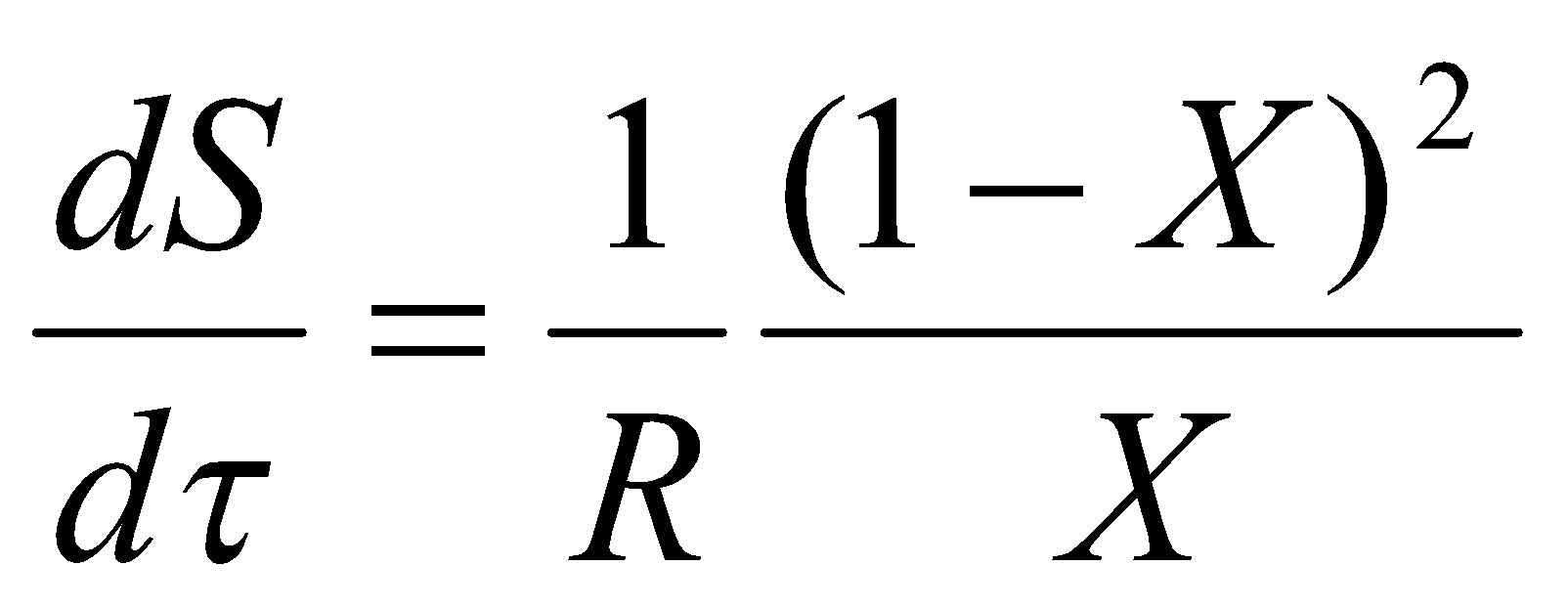
 .
.
Математически вышеприведённая формула совпадает с общепринятой. Предложение использовать отношение температур Х в явной форме основано главным образом на том, чтобы избежать произведения температур, поскольку такое произведение не имеет физического смысла. В приведённом уравнении отсутствует выражение градиента температур, но характер изменения температуры определяется как геометрическими особенностями теплопроводящей среды, так и значением коэффициента теплопроводности, в общем случае нелинейно зависящего от температуры, а эти факторы следует учитывать при определении RQ.
Максимальное производство энтропии при прочих равных условиях достигается при простом рассеивании высокопотенциальной энергии в низкопотенциальную окружающую среду. Производство энтропии будет меньше, если в процессе данного рассеивания часть тепловой энергии преобразовывается в иные формы, например механическую или химическую, либо плотность тепловой энергии локально поддерживается на уровне, превышающем уровень плотности энергии окружающей среды. Поэтому предлагается разность изменения максимально возможной и изменения данной энтропии отождествить с изменением негэнтропии:
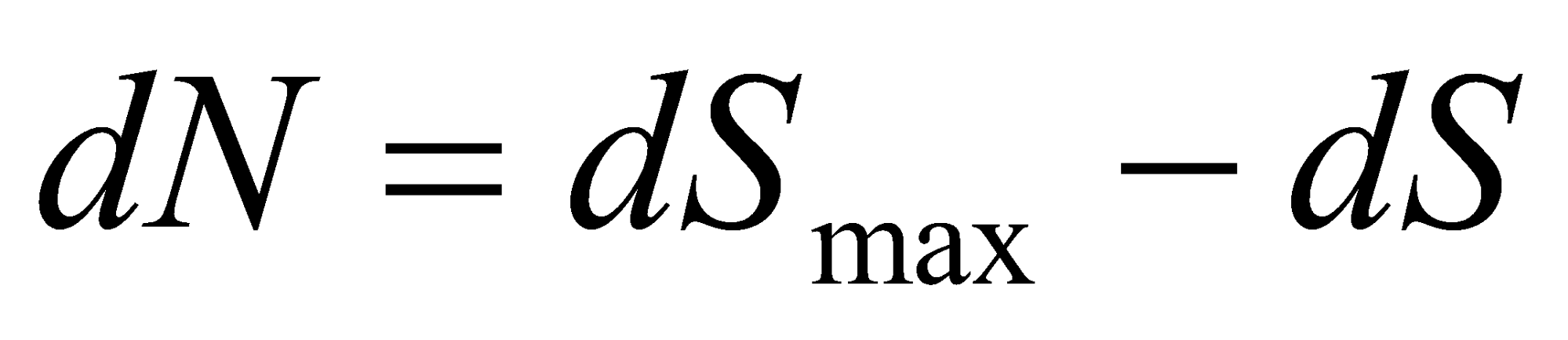
 .
.
В [2] введено понятие энтропийной эффективности
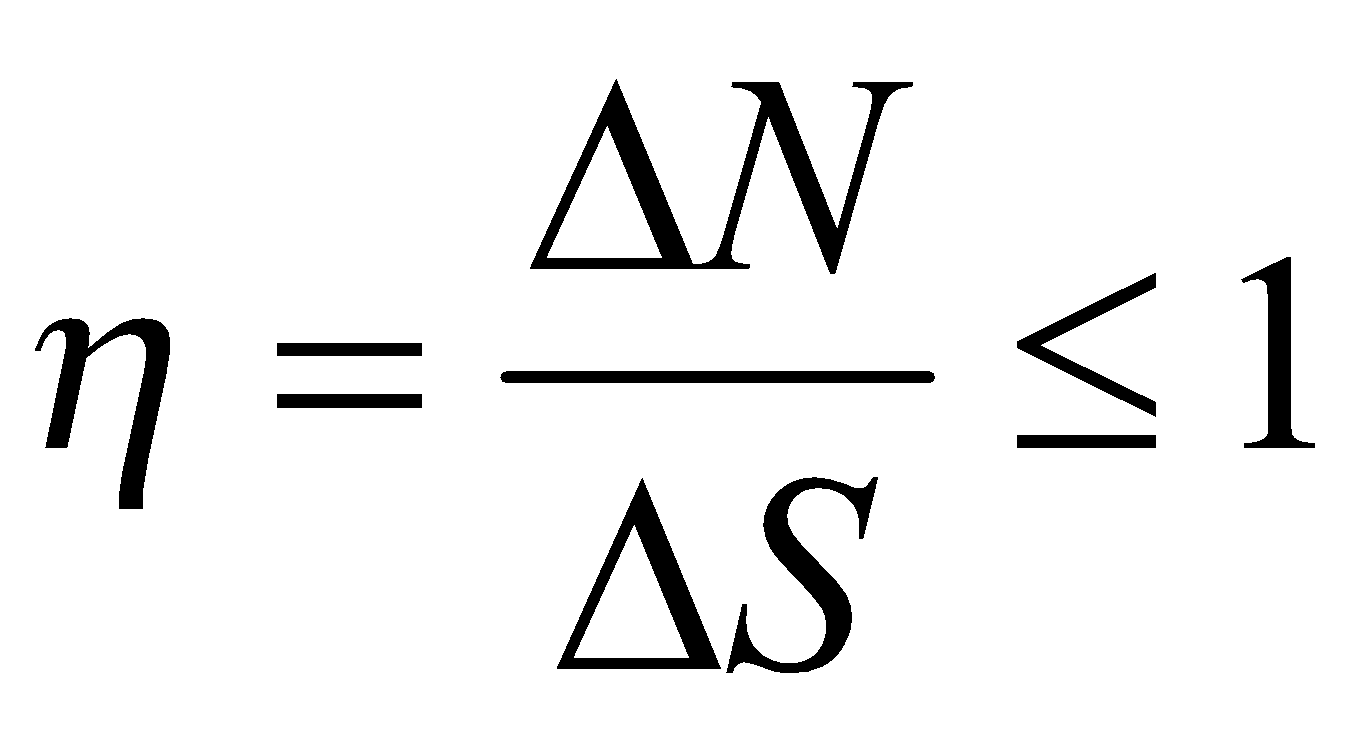
 ,
,
характеризующей степень необратимости процесса упорядочения некоторой системы и при приближении к обратимому процессу 
 . Введём аналогичное отношение изменения негэнтропии к максимальному изменению энтропии и свяжем данное отношение с энтропийной эффективностью теплофизического процесса:
. Введём аналогичное отношение изменения негэнтропии к максимальному изменению энтропии и свяжем данное отношение с энтропийной эффективностью теплофизического процесса:
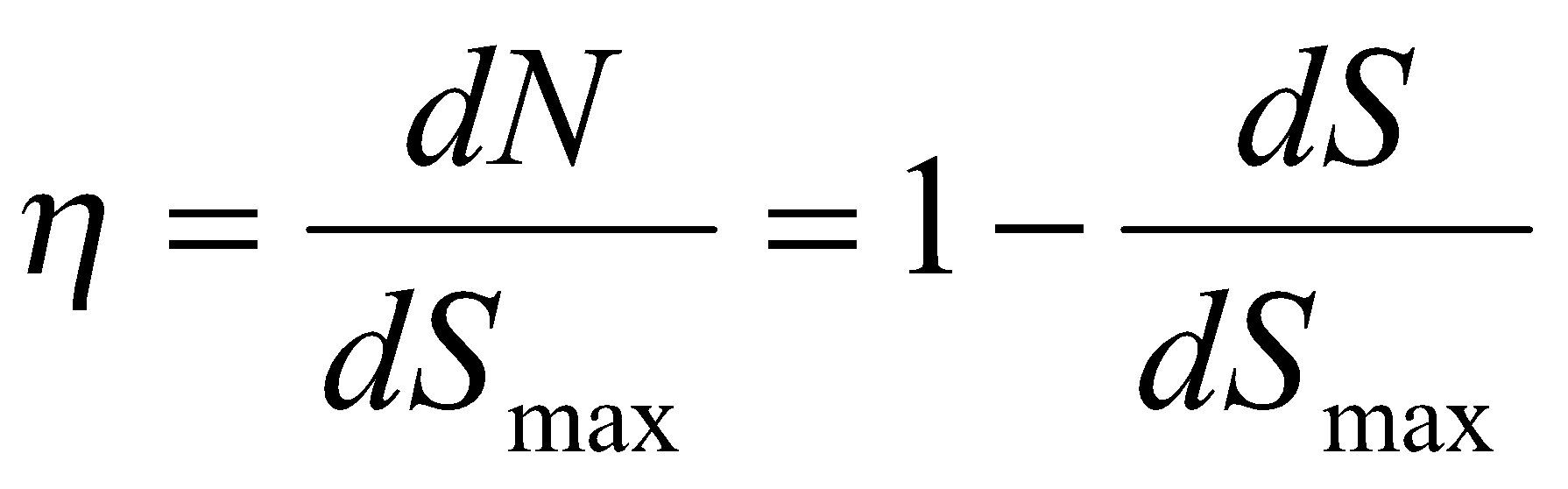
 .
.
Для иллюстрации введённого термина рассмотрим несколько простых примеров.
Отапливаемое помещение, рассеивающее теплоту в окружающую среду
Задача определения энергетической эффективности процесса отопления помещения остается нерешённой, поскольку применение коэффициента полезного действия для данного процесса не представляется возможным вследствие отсутствия полезной механической работы. Определение энтропийной эффективности позволяет разработать критерий, характеризующий степень тепловой эффективности отапливаемых зданий.
Рассмотрим модель простейшей системы отапливаемого помещения или здания, состоящего из ограждающих конструкций и отопительного прибора (батареи). Отопительный прибор характеризуется средней температурой теплоносителя Тб и полным коэффициентом термического сопротивления теплопередаче Rб с учетом площади теплообмена Fб. Помещение характеризуется средней температурой воздуха Тзд, постоянной по всему объёму, коэффициентом термического сопротивления теплопередаче стен Rст с учётом площади Fст. Окружающая среда по отношению к помещению представляет собой термостат с заданной температурой Токр. Воздух внутри помещения полагается находящимся в состоянии равновесия. Система является стационарной; температура теплоносителя изменяется в соответствии с изменением температуры окружающей среды с целью поддержания температуры внутри помещения постоянной, заданной исходно.
Первым этапом расчёта является определение тепловых потерь помещения, в силу стационарности рассматриваемого процесса равных тепловой мощности отопительных приборов:
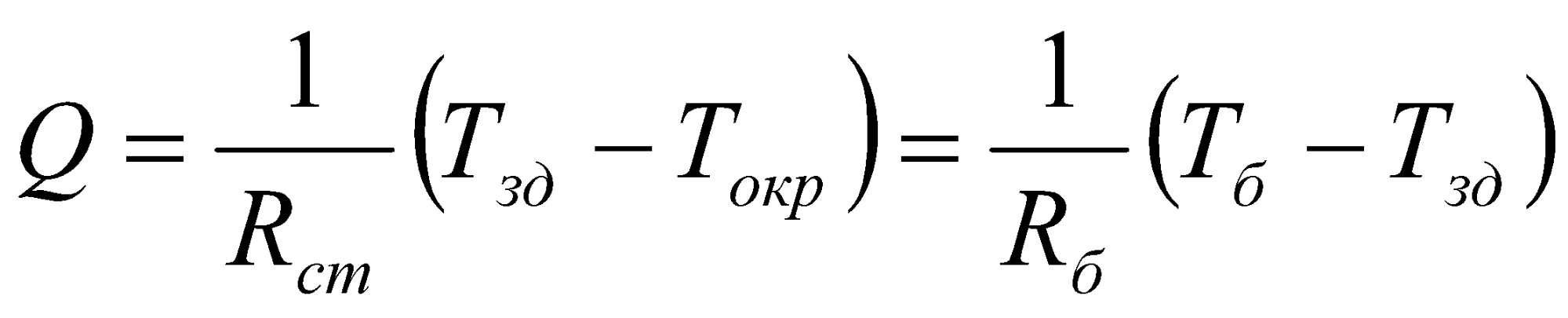
 ,
,
откуда рассчитывается средняя температура теплоносителя Tб, движущегося в отопительной батарее и по сути являющегося внутренним источником энергии для рассматриваемой системы.
Следующий этап заключается в определении суммарного производства энтропии.
Определим производство энтропии при передаче теплоты от отопительного элемента внутреннему воздуху:
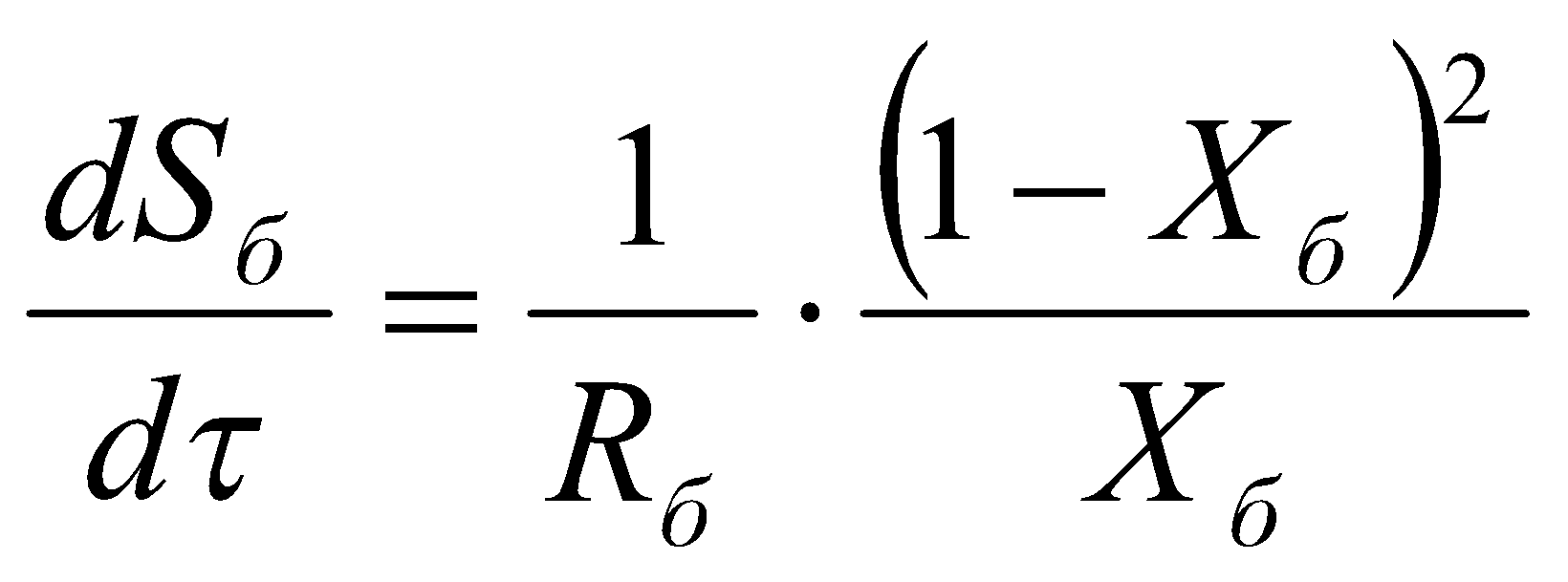
 ,
,
где 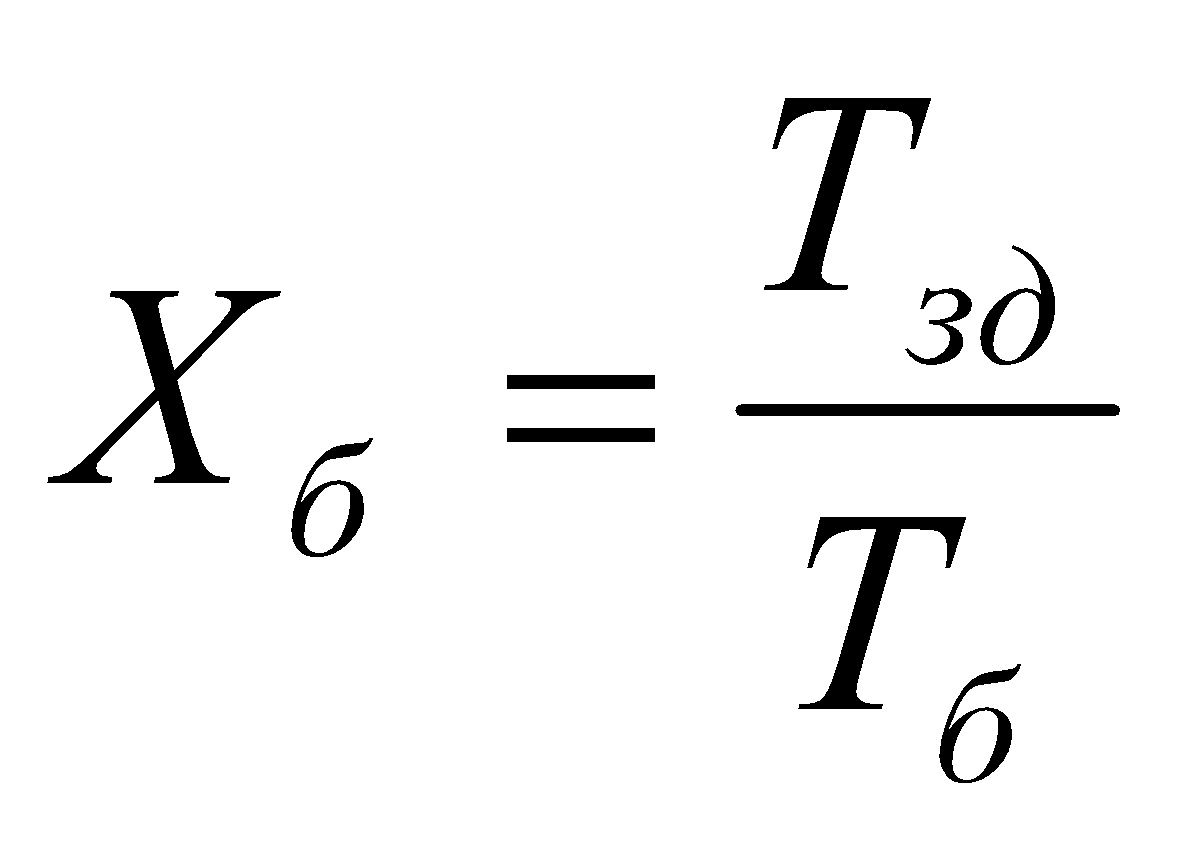
 .
.
Аналогично, производство энтропии при передаче теплоты от внутреннего воздуха наружу через ограждающие конструкции:
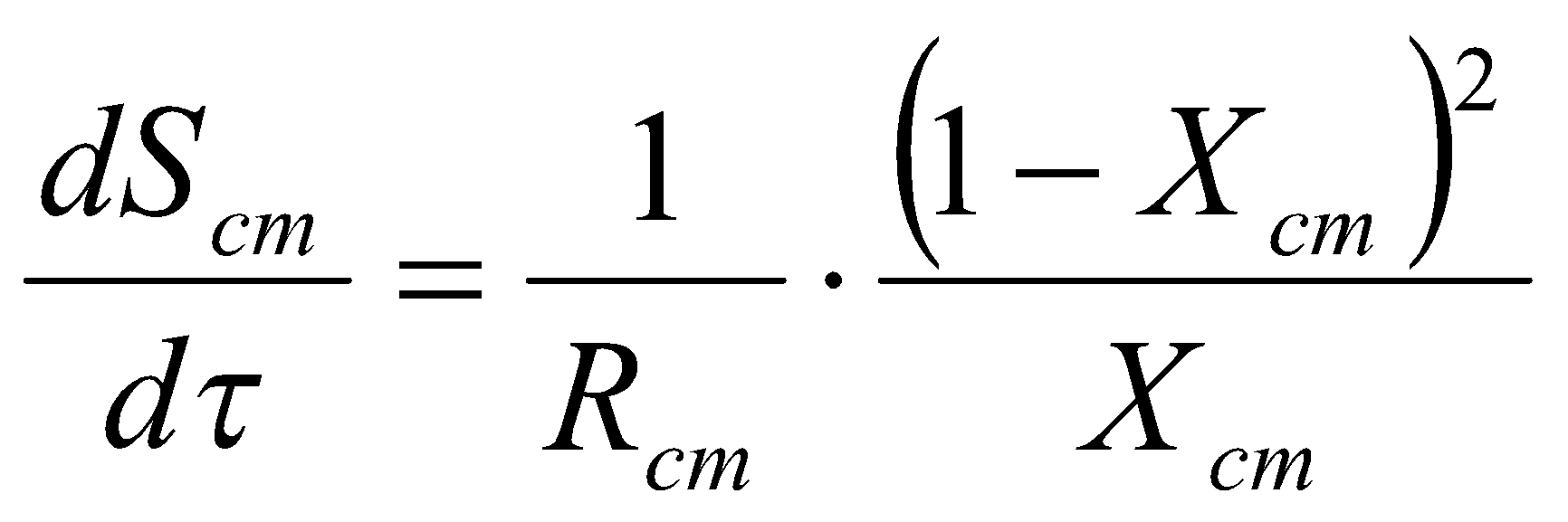
 ,
,
где 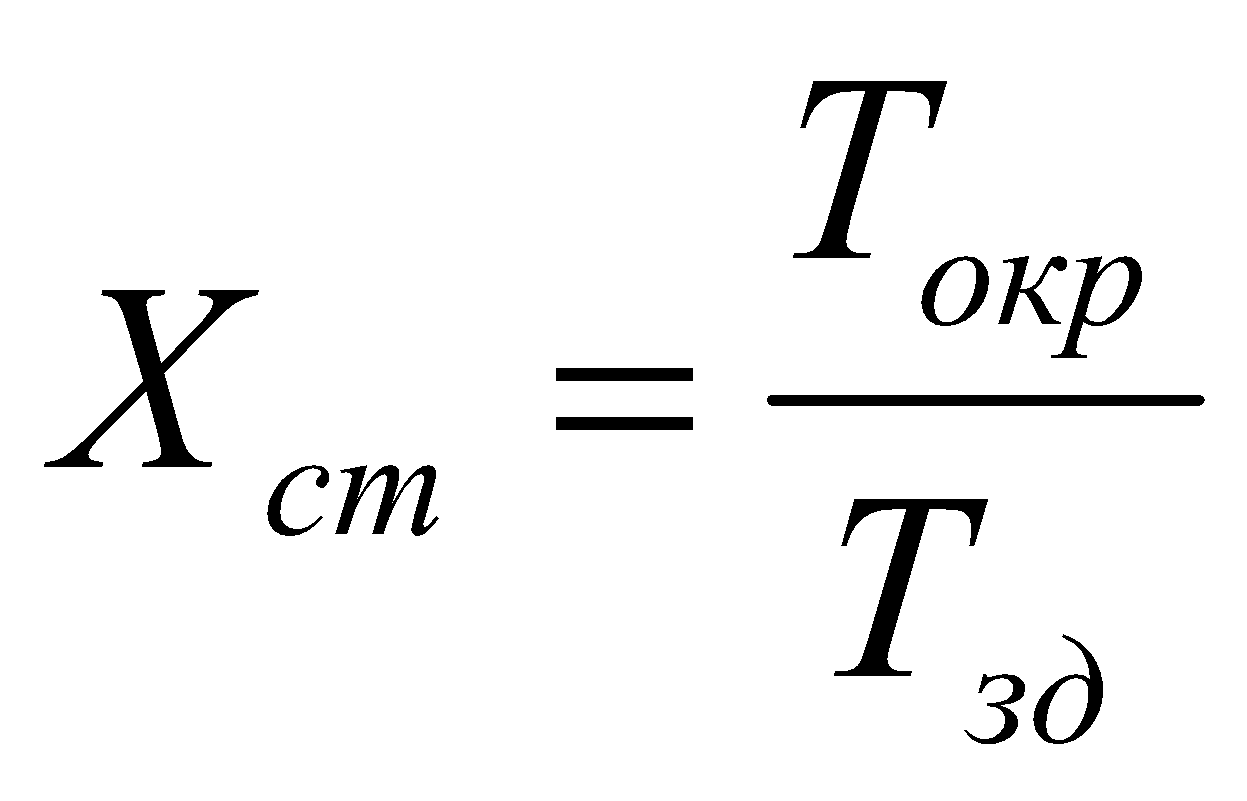
 .
.
Также введём минимальное отношение температур:
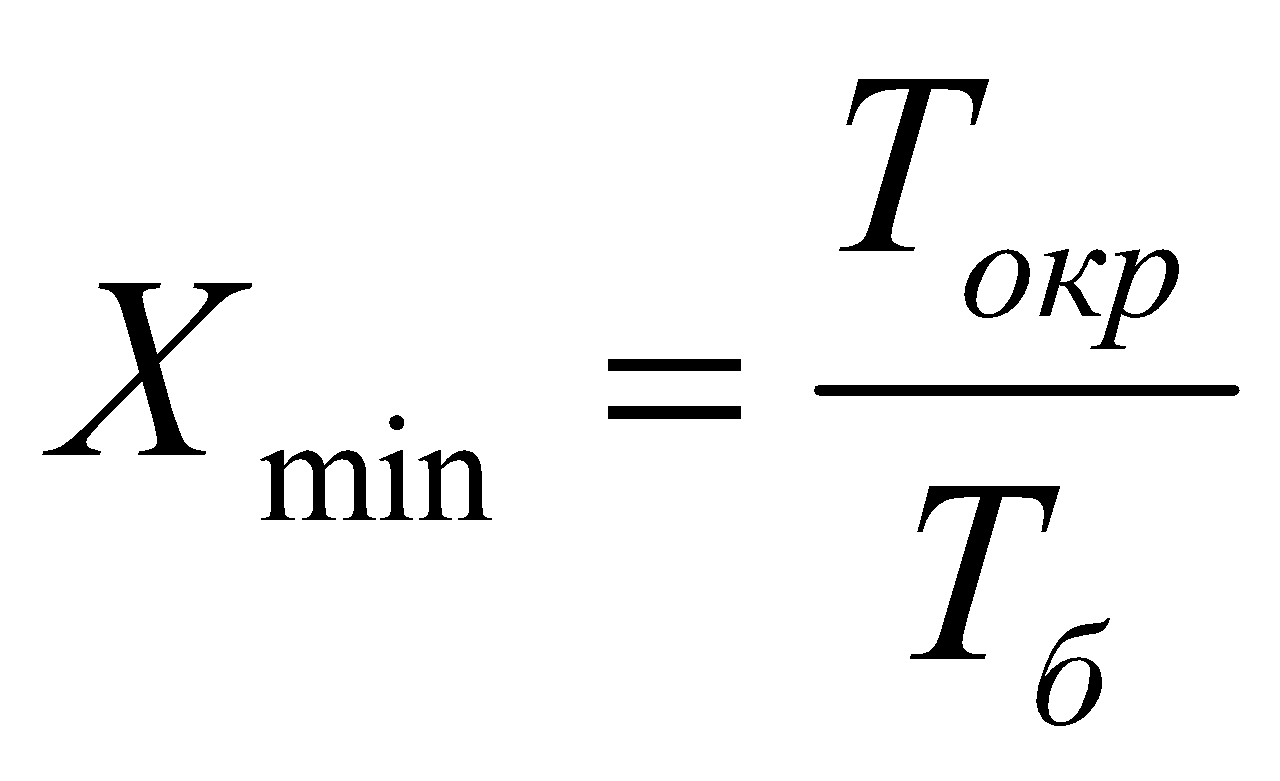
 .
.
Введём термин «термически предельно неэффективное здание». Таким зданием будем считать помещение без стен, или, что математически эквивалентно, со стенами, имеющими нулевое термическое сопротивление теплопередаче. В этом случае температура в помещении будет равна температуре окружающей среды, являющейся термостатом (Тзд=Токр). Производство энтропии стенами, соответственно, равно нулю, а общее производство энтропии определится термическим сопротивлением только отопительной батареи и будет являться максимально возможным в заданном температурном диапазоне:
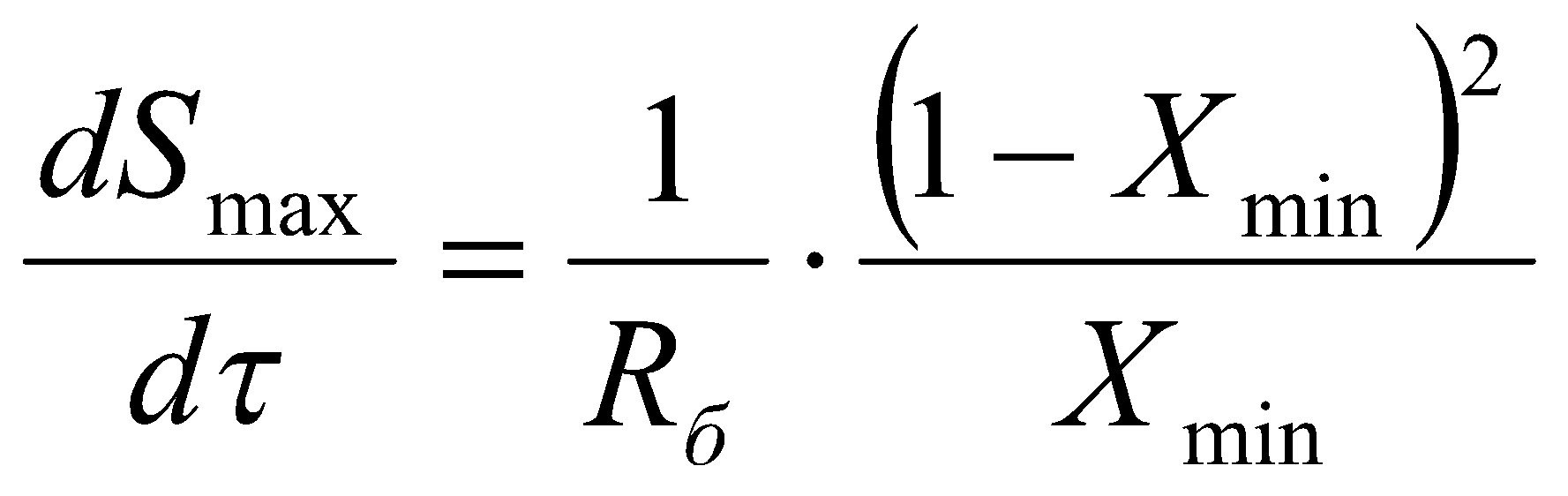
 .
.
С другой стороны, предельно эффективным зданием следует считать здание с адиабатными стенами, имеющими бесконечно большое значение термического сопротивления теплопередаче и поэтому не имеющее тепловых потерь. В данном случае отсутствуют тепловые потоки, как к внутреннему воздуху, так и к наружному, и, следовательно, производство энтропии равно 0.
В результате численного анализа было обнаружено, что существует величина, принимающая значения от 0 до 1 и в явной форме не зависящая от температур (если в первом приближении принять, что температура не оказывает влияния на коэффициенты теплопроводности и теплоотдачи):
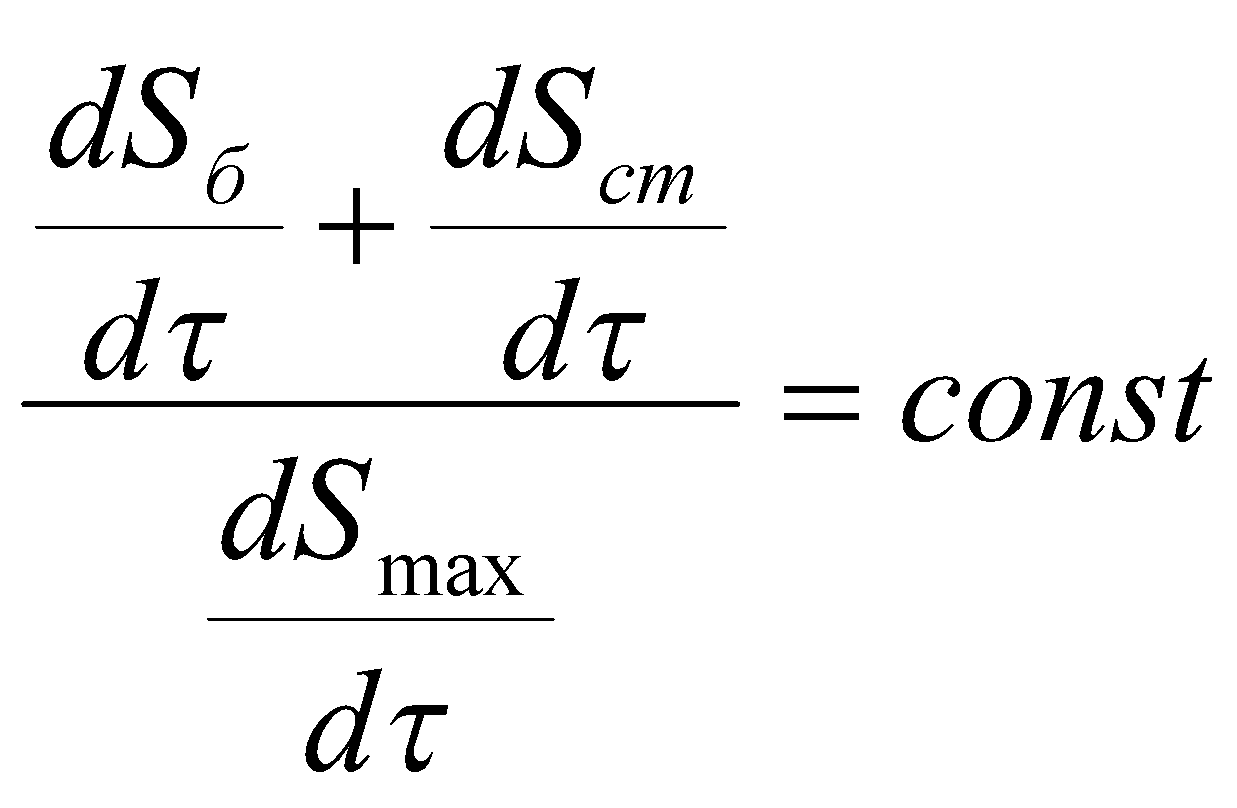
 .
.
Эта величина увеличивается с ростом полного термического сопротивления отопительного прибора и уменьшается с ростом полного термического сопротивления стен. На основании данного эффекта, а также на основании вышеизложенных соображений об энтропийной эффективности, предлагается использовать следующий параметр в качестве показателя энтропийной эффективности отапливаемого помещения:
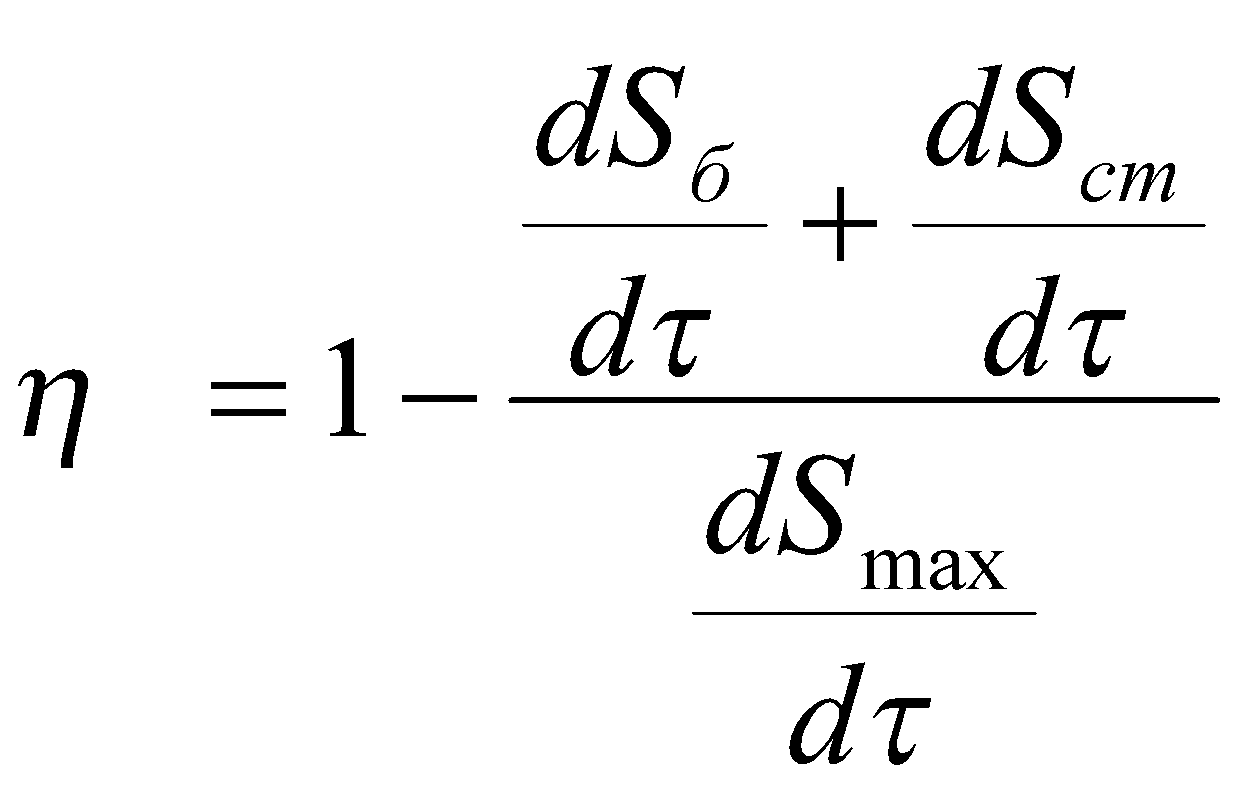
 .
.
При этом производство негэнтропии равно
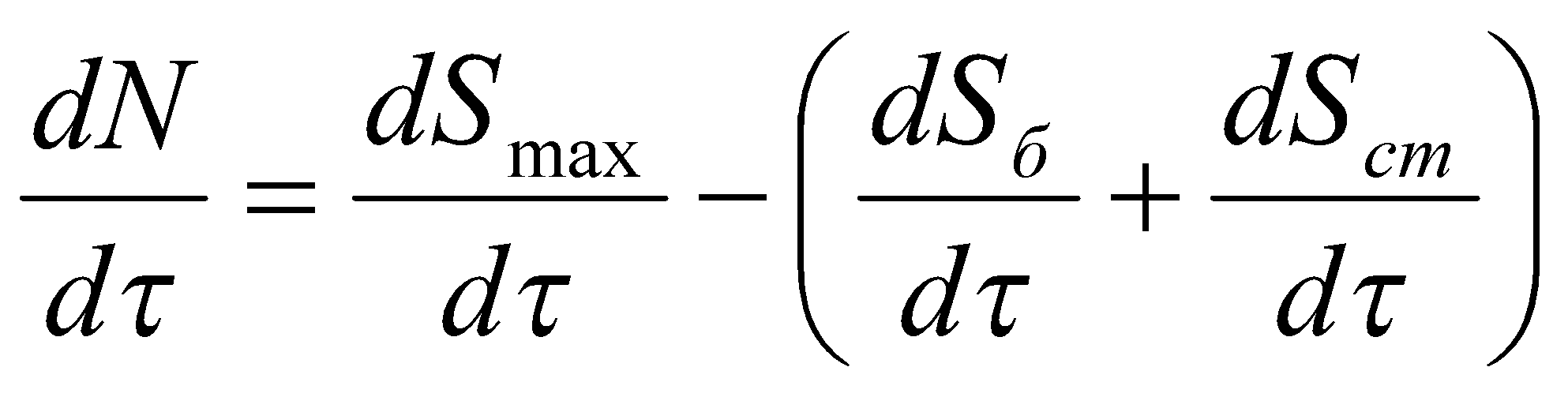
 .
.
Физический смысл производства негэнтропии отапливаемым помещением связан с локальным поддержанием значения температуры выше, чем температура окружающей среды (Tзд>Tокр). Необходимо отметить, что в отличие от соотношения 
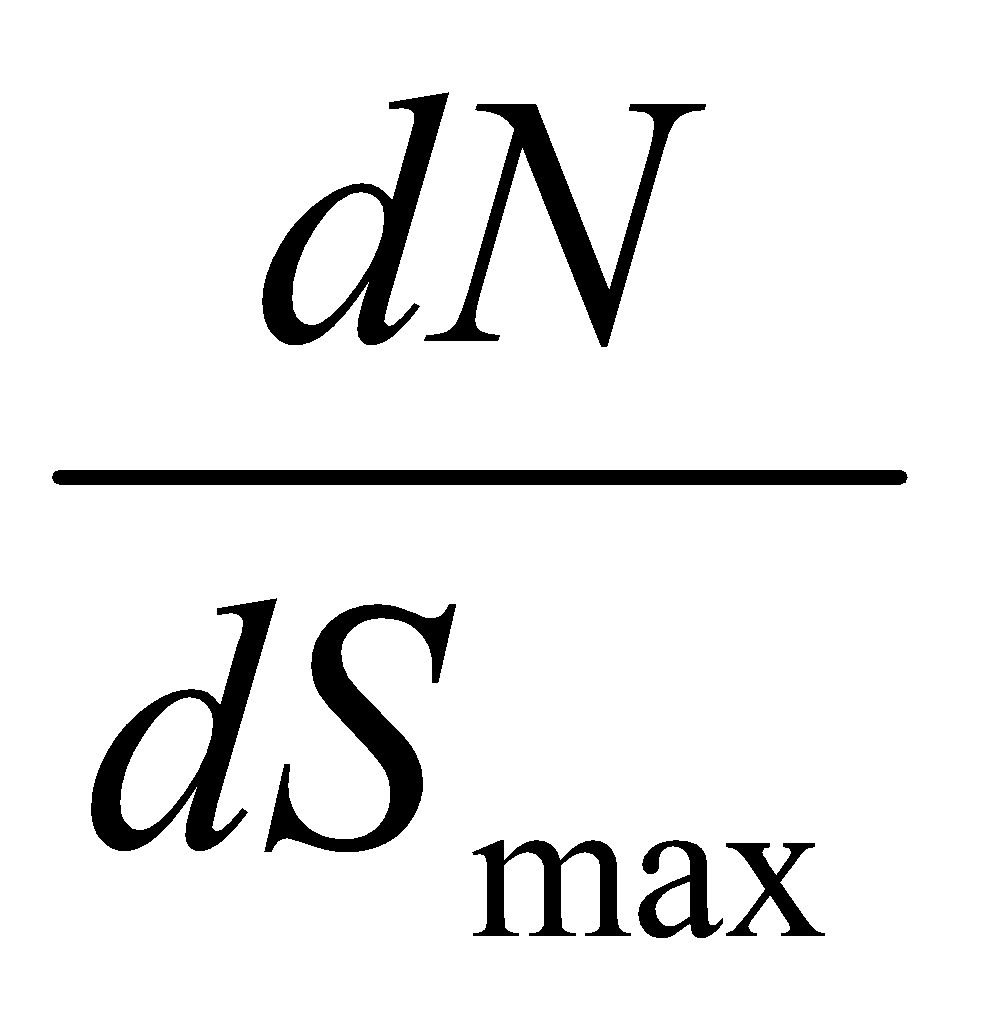 , соотношение
, соотношение 
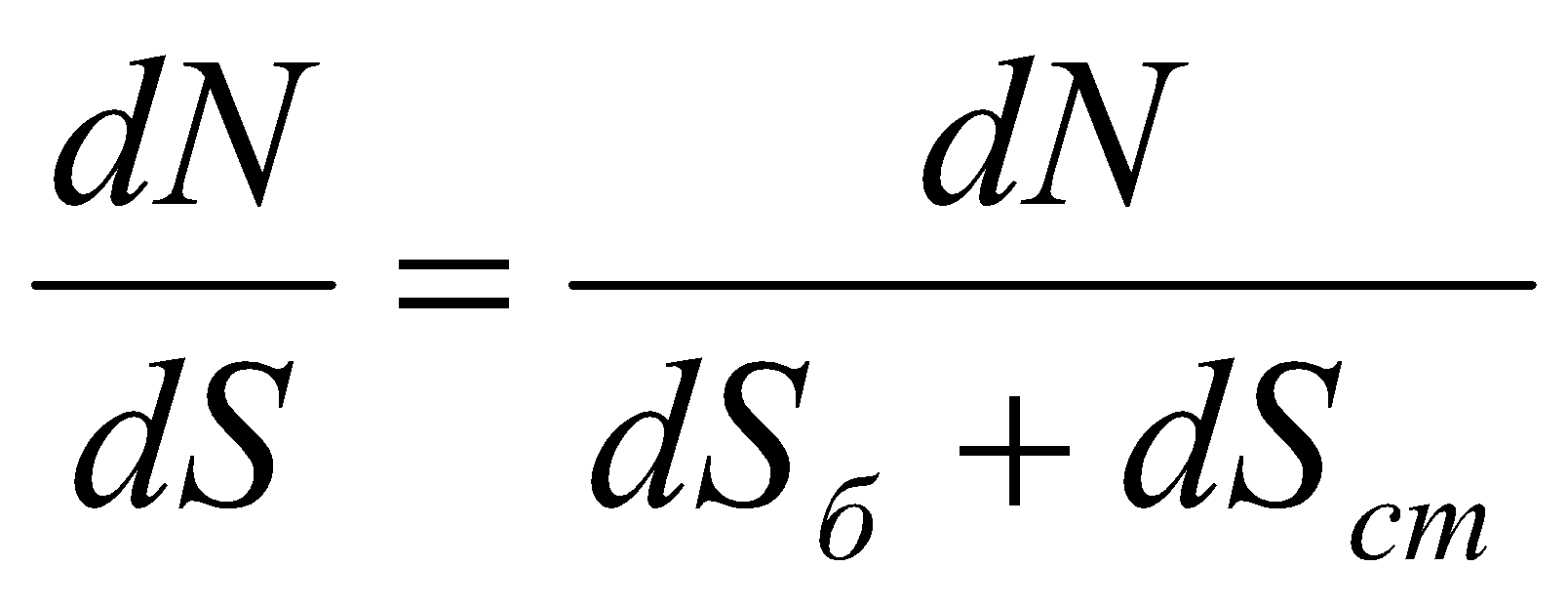 не является постоянным и принимает значения как меньше, так и больше единицы, и поэтому не может быть мерой энтропийной эффективности.
не является постоянным и принимает значения как меньше, так и больше единицы, и поэтому не может быть мерой энтропийной эффективности.
Энтропийная эффективность зависит от температур наружного и внутреннего воздуха и теплоносителя в системе отопления лишь в той мере, в какой от этих температур зависят коэффициенты теплоотдачи и теплопроводности. Следовательно, эффективность помещения зависит только от теплофизических свойств отопительных приборов, ограждающих конструкций и свойств теплоносителей, и численно равно следующему соотношению:
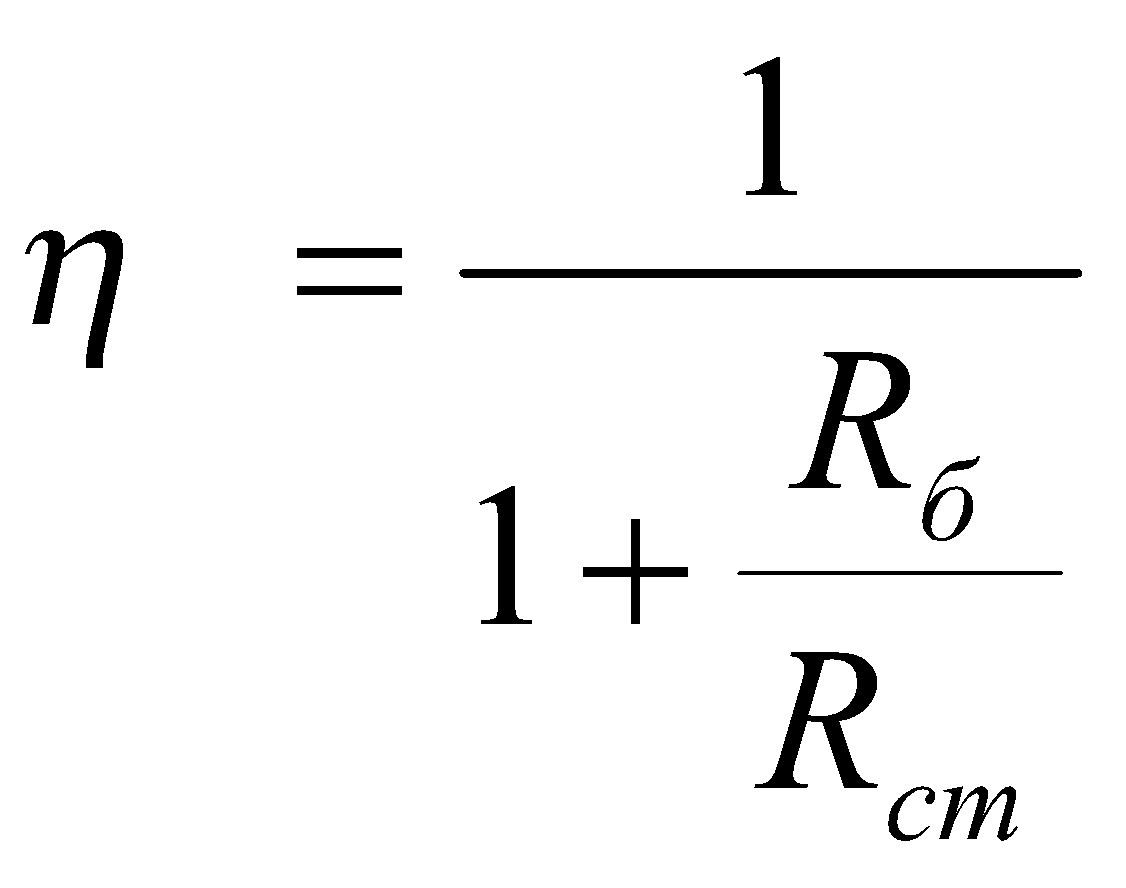
 .
.
Полученный критерий характеризует степень энтропийной эффективности процесса поддержания температуры в отапливаемом помещении.
Очевидно, повысить тепловую эффективность здания можно двумя путями: увеличением термического сопротивления ограждающих конструкций Rст и уменьшением термического сопротивления отопительных приборов Rб. Если не интенсифицировать теплоотдачу от отопительных приборов, то снижение Rбможно достигнуть простым увеличением площади теплообмена, наращивая количество секций отопительных батарей. В этом случае неизменная тепловая нагрузка остаётся при условии уменьшения средней температуры греющего теплоносителя, то есть снижении параметра XБ и, соответственно, снижении производства энтропии при передаче теплоты от отопительного элемента внутреннему воздуху. Однако следует иметь в виду, что наращивание количества секций, во-первых, приводит к увеличению металлоемкости, во-вторых, к повышенным затратам на транспорт греющего теплоносителя.
Результаты численного эксперимента представлены на рисунке 1.

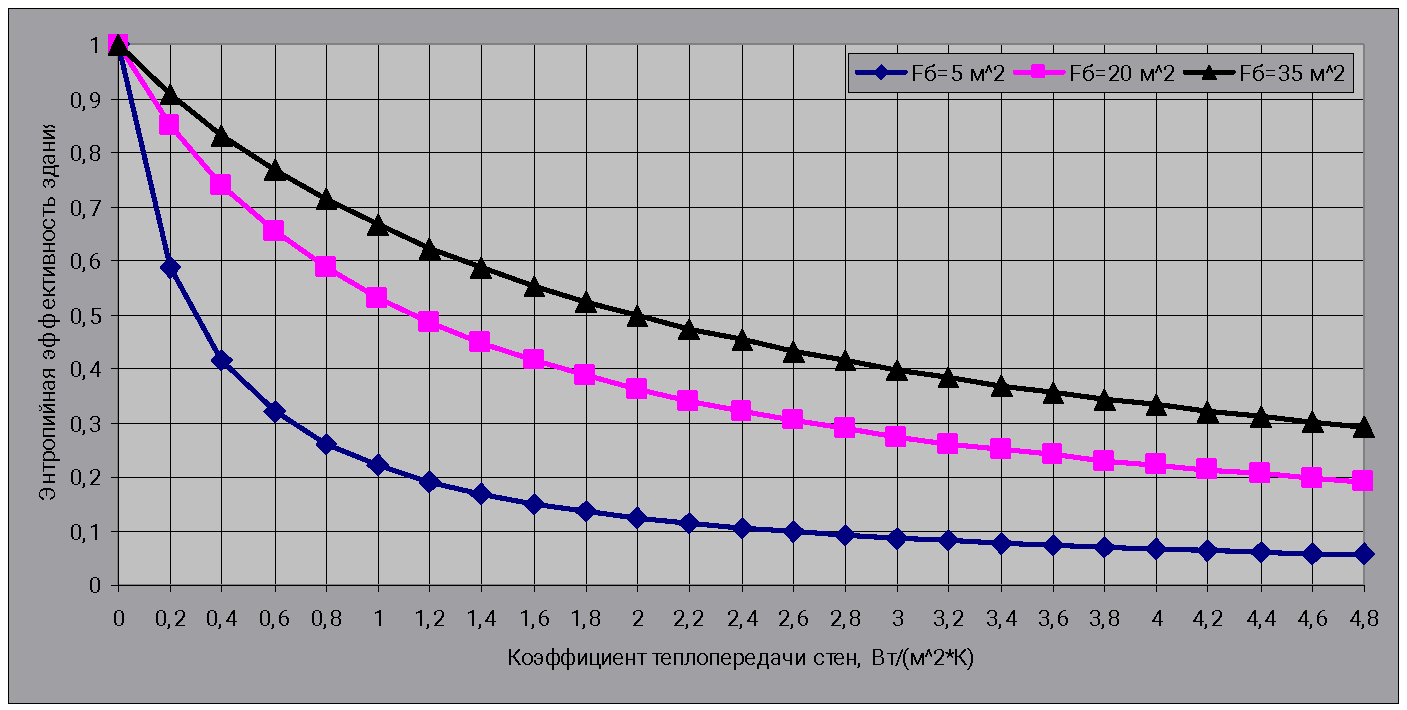
Рисунок 1 – Зависимость энтропийной эффективности здания от коэффициента теплопередачи ограждающих конструкций при различных величинах площадей теплообмена отопительных приборов.
Паровая турбина, совершающая работу
Теперь применим принцип энтропийной эффективности, рассматривая цикл паротурбинной установки, которая работает в диапазоне температур от Т1 до Т2. Пусть к циклу подводится теплота в количестве Q1, и к холодному источнику отводится теплота Q2, кроме того, в процессе совершается полезная работа L=Q1-Q2.
Изменение энтропии в процессе расширения примет вид:
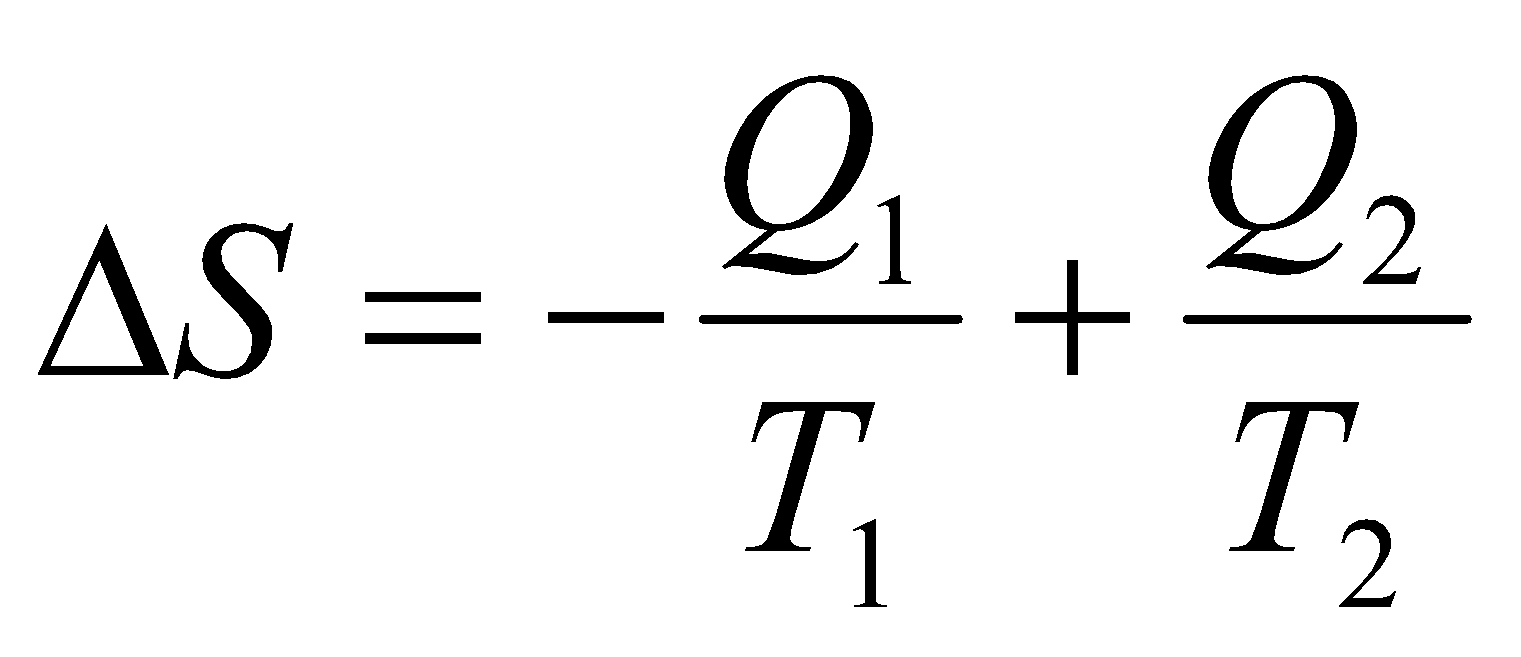
 .
.
Как известно, идеальный адиабатный процесс расширения пара в турбине является изоэнтропным, то есть 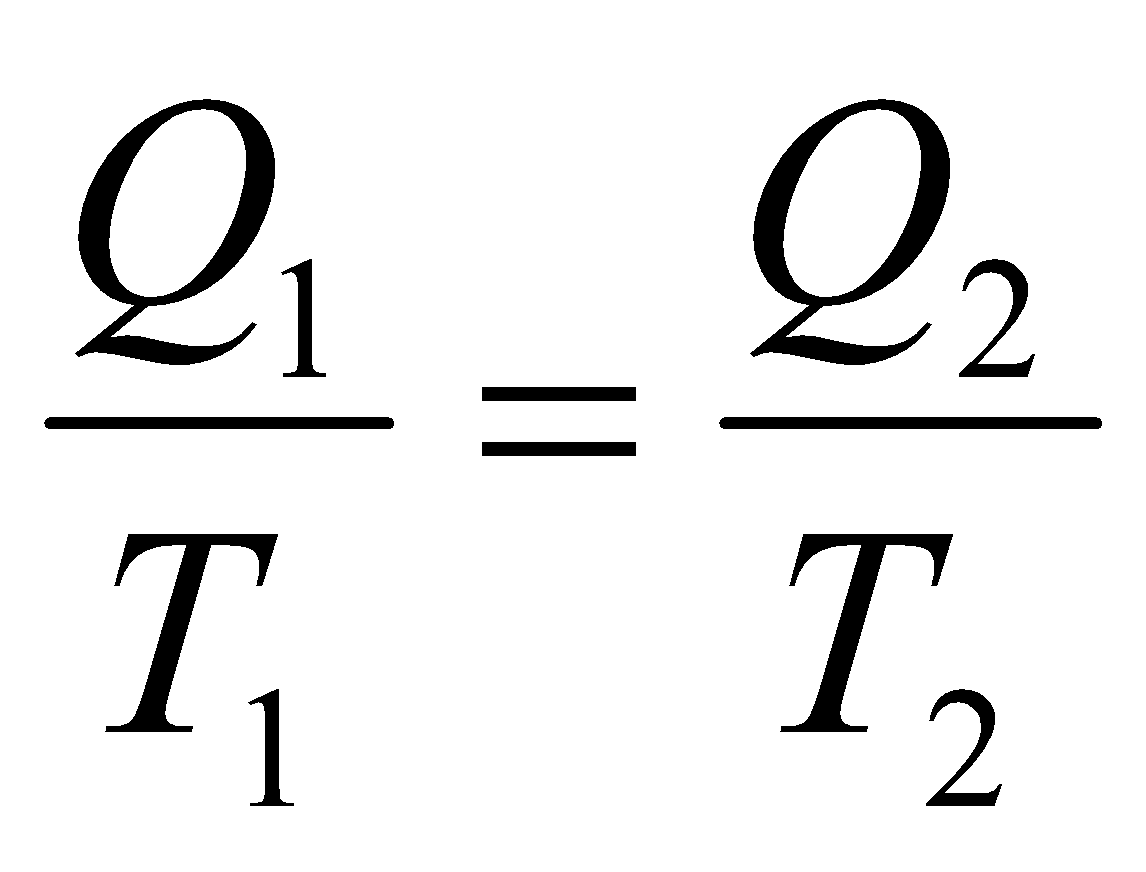
 , и ΔS=0, но реальный процесс характеризуется неравенством ΔS>0.
, и ΔS=0, но реальный процесс характеризуется неравенством ΔS>0.
В случае если полезная работа не производится, то есть Q2=Q1, вся подведенная высокопотенциальная тепловая энергия бесполезно рассеивается в низкопотенциальную окружающую среду, тогда изменение энтропии максимально:
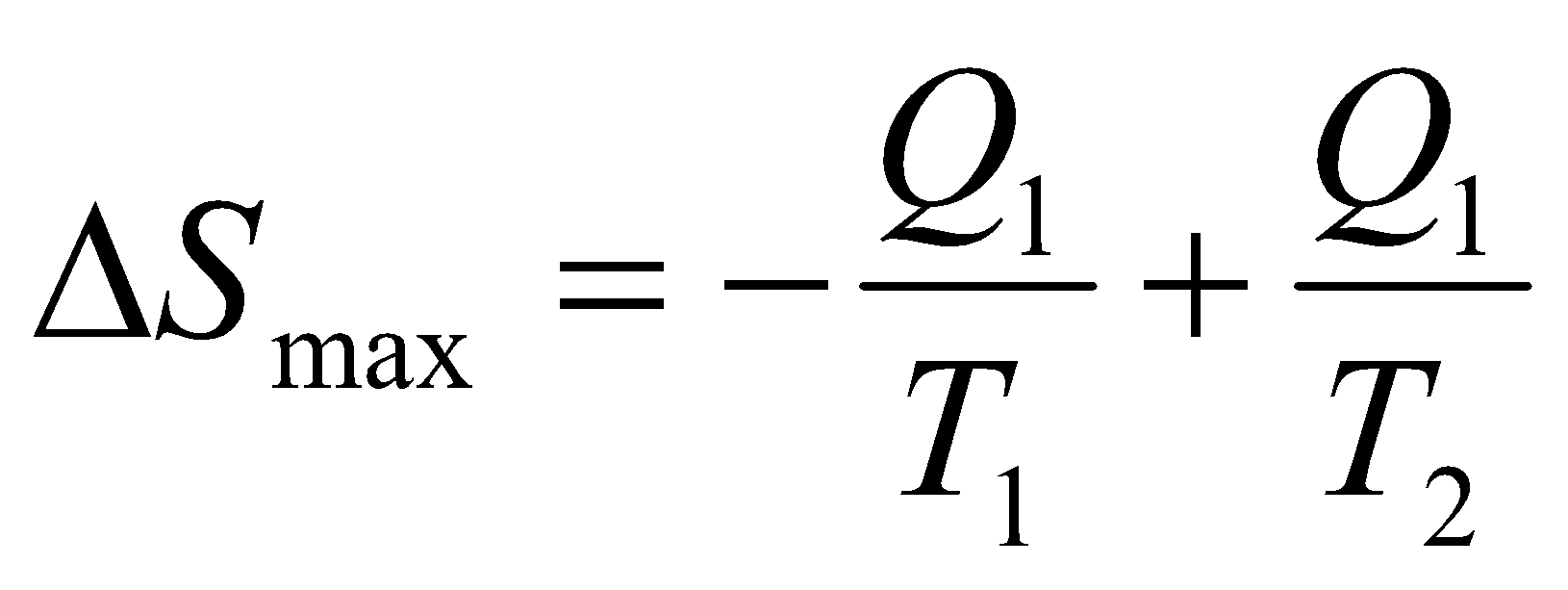
 .
.
Разницу между максимальным и текущим изменением энтропии назовём негэнтропией, связав данное понятие с превращением тепловой энергии в иную форму, в данном случае в механическую энергию вращения ротора турбины:
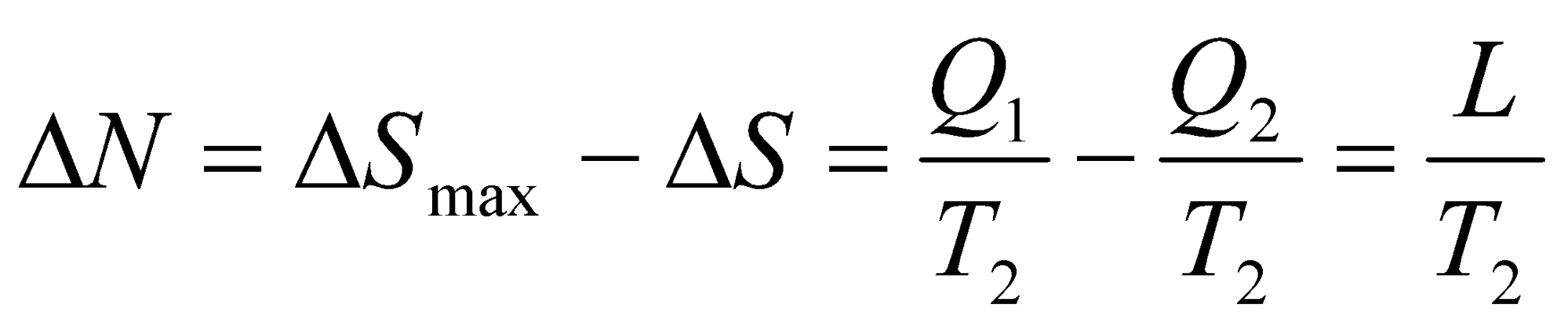
 .
.
Энтропийная эффективность примет вид:
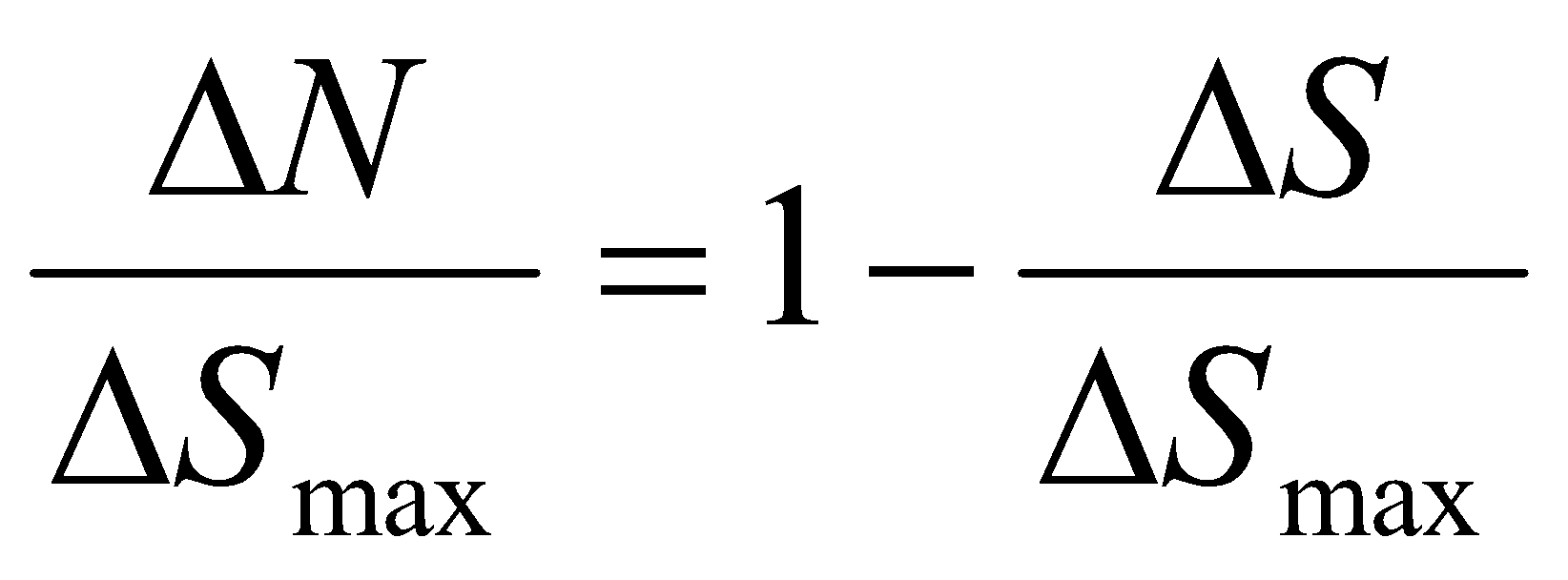
 ,
,
откуда нетрудно получить следующую зависимость:
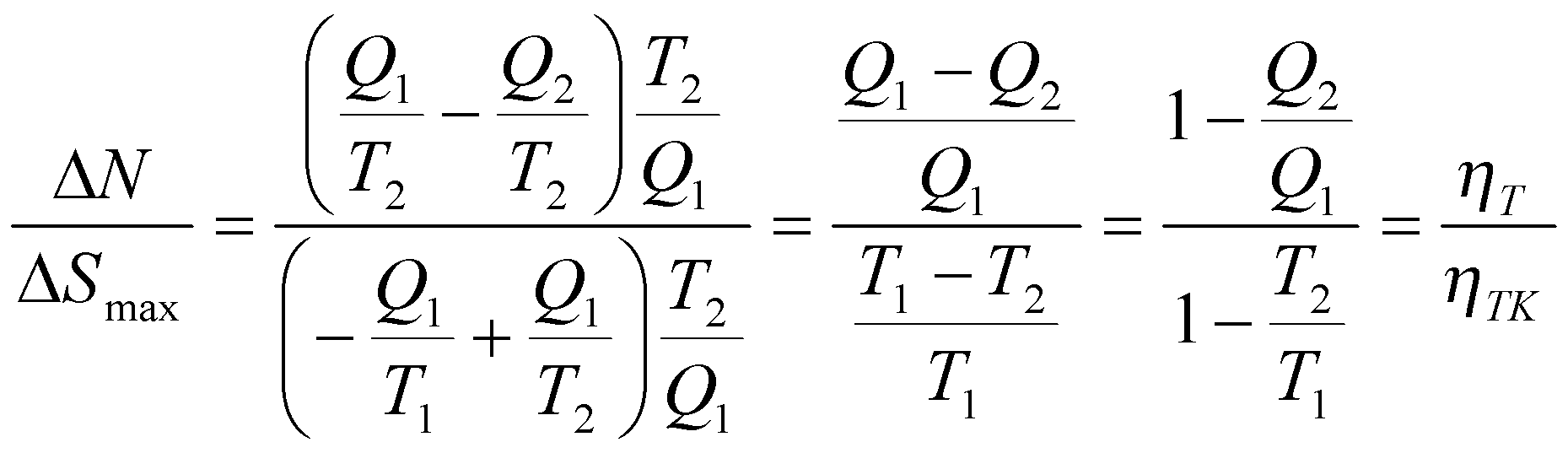
 .
.
Таким образом, энтропийная эффективность паротурбинного цикла равна отношению КПД реального цикла (например, цикла Ренкина) к термическому КПД прямого цикла Карно для заданного диапазона температур. Другими словами, энтропийная эффективность показывает, насколько реальный цикл приближается к идеальному циклу Карно.
Тепловой насос, потребляющий работу
Для определения энтропийной эффективности обратного цикла рассмотрим цикл теплонасосной установки, работающей в диапазоне температур от Т2 до Т1, причём Т1>Т2. Подводимая теплота равна Q2, затрачиваемая на привод компрессора работа равна L, теплота, отводимая потребителю, принимает значение Q1=L+Q2.
Изменение энтропии в процессе сжатия:
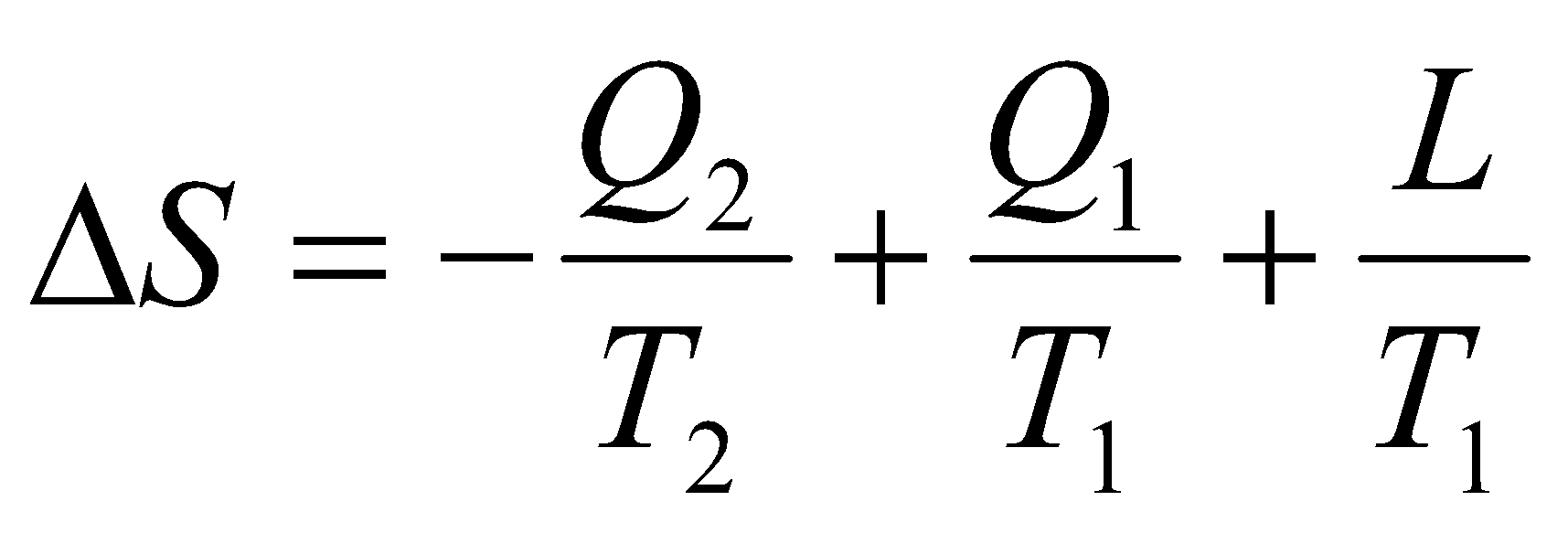
 .
.
В случае, если внешняя работа необратимо преобразуется в низкопотенциальную теплоту и рассеивается, повышения температуры не происходит, (Т2=Т1), и тогда изменение энтропии максимально:

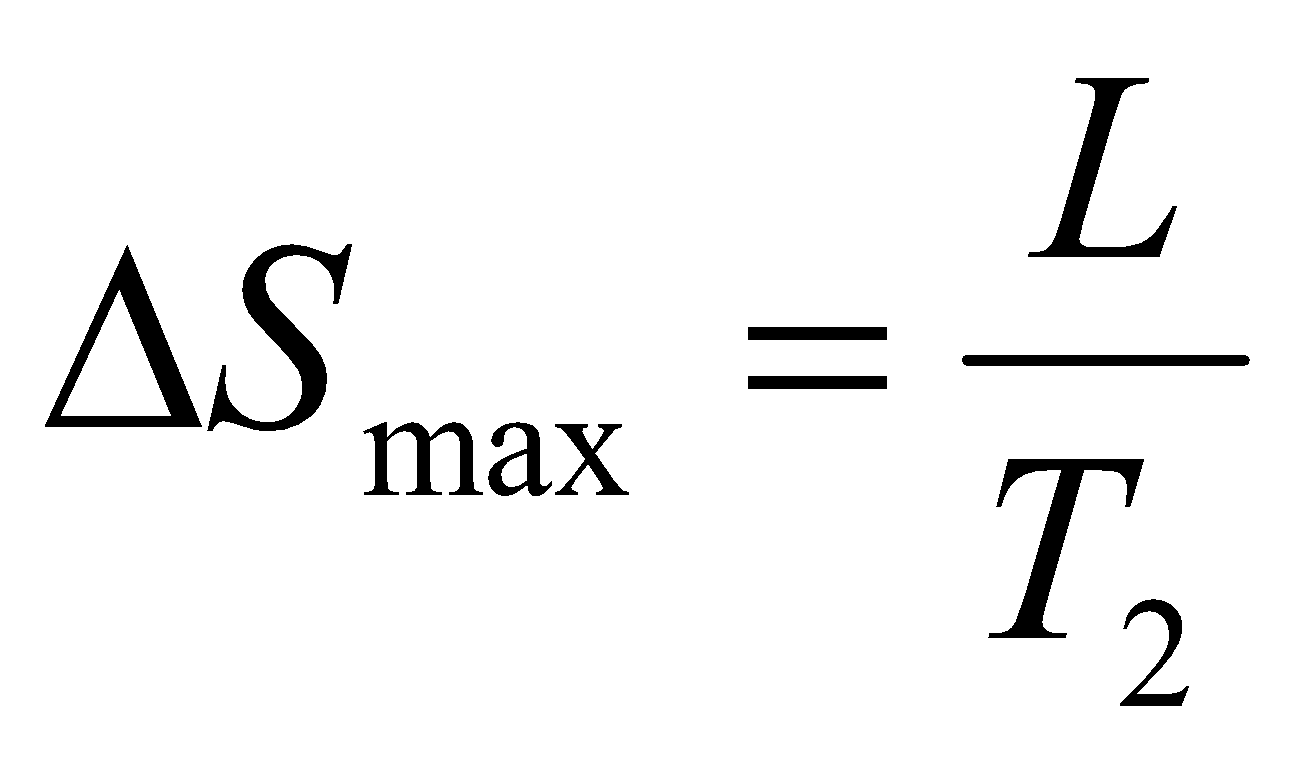 .
.
Разницу между максимальным и текущим изменением энтропии аналогично назовём негэнтропией, связав её в данном случае с передачей теплоты от низкопотенциального источника высокопотенциальному с учётом дополнительного нагрева за счёт преобразования работы в теплоту:
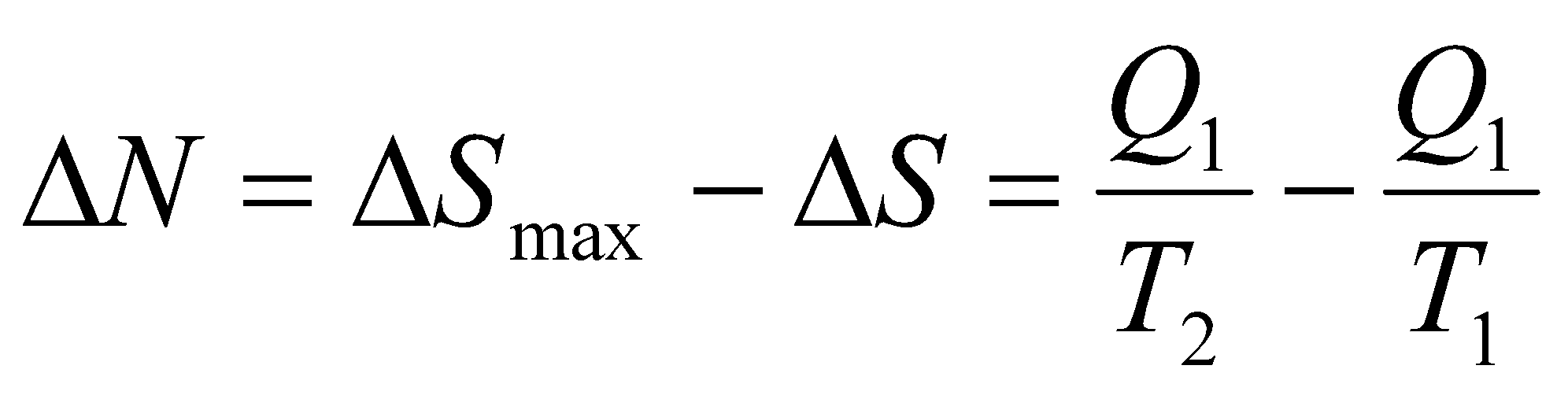
 .
.
Энтропийная эффективность в общем случае принимает аналогичную предыдущей форму:
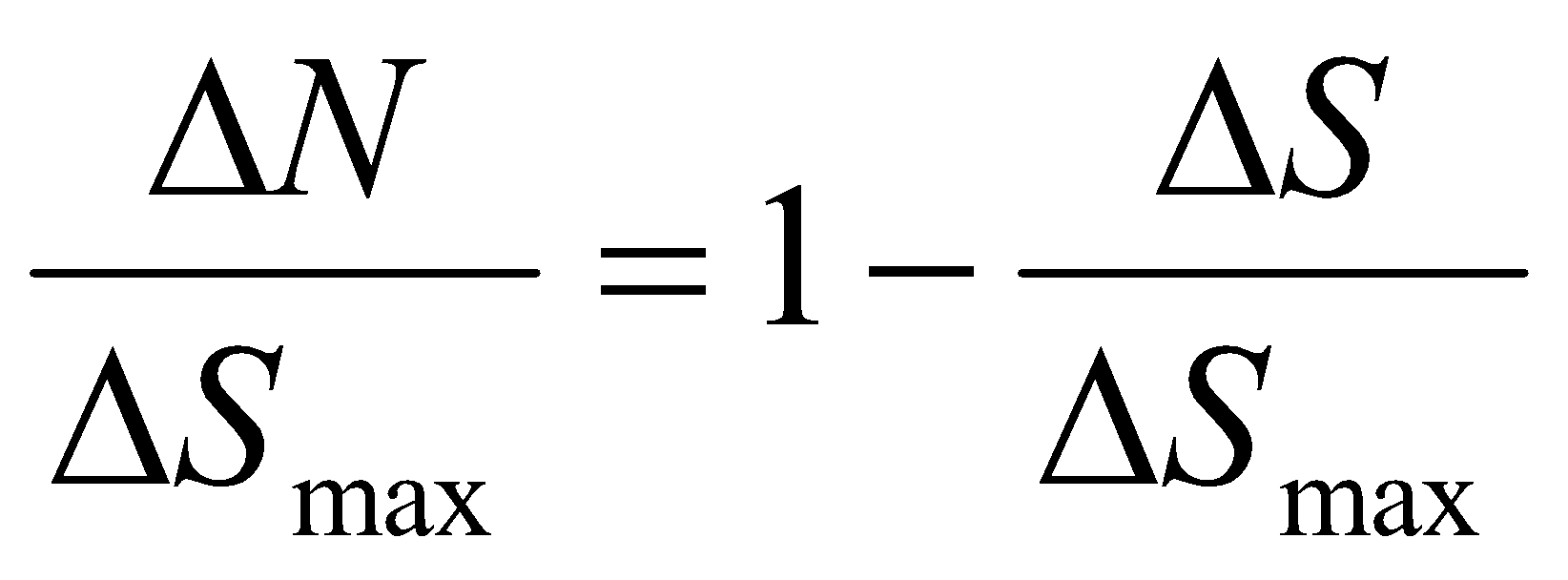
 .
.
И далее:
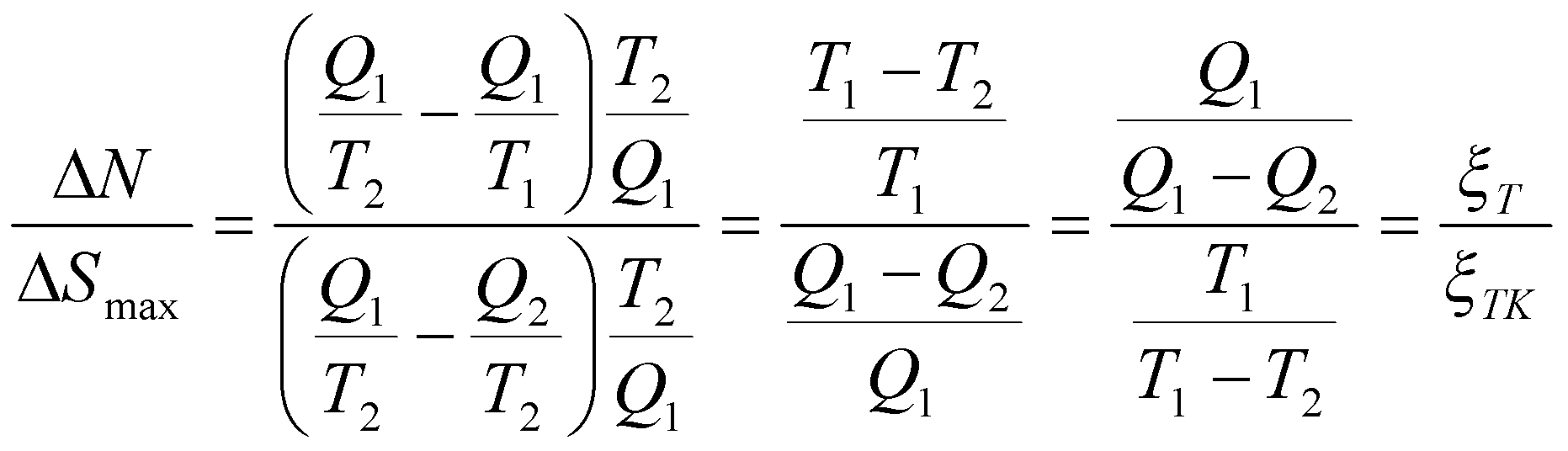
 .
.
Таким образом, энтропийная эффективность цикла теплового насоса равна отношению коэффициента теплоиспользования реального цикла к коэффициенту теплоиспользования обратного цикла Карно для заданного диапазона температур. Как и в предыдущем примере, энтропийная эффективность показывает, насколько совершенен реальный цикл по отношению к обратному обратимому циклу Карно в заданном диапазоне температур.
Предложенный метод определения энтропийной эффективности теплоэнергетических объектов даёт возможность численно рассчитать относительную степень тепловой эффективности различных систем, в том числе с преобразованием энергии в различные формы. Энтропийная эффективность наряду с общеизвестными параметрами позволяет определить относительную степень совершенства объектов, потребляющих тепловую энергию, в том числе работающих по обратному циклу, таких как тепловые насосы.
Список литературы / References
1. Пригожин И. Современная термодинамика. От тепловых двигателей до диссипативных структур [Текст] : учебное издание : [пер. с англ.] / И. Пригожин, Д. Кондепуди – М.: Мир, 2002. – 461 с., ил. ISBN 5-03-003538-9.
2. Поплавский Р.П. Термодинамика информационных процессов [Текст] : монография / Р.П. Поплавский – М.: Наука. Главная редакция физико-математической литературы, 1981. – 256 с., ил.
3. Квасников И.А. Термодинамика и статистическая физика [Текст] : учебное пособие в 3 ч. / И.А. Квасников – М.: Едиториал УРСС, 2010. ISBN 978-5-354-01305-0.
4. Базаров И.П. Заблуждения и ошибки в термодинамике [Текст] : Изд. 2-е, испр. / И.П. Базаров – М.: Едиториал УРСС, 2003. – 120 с. ISBN 5-354-00391-1
5. Бриллюэн Л. Наука и теория информации [Текст] : [пер. с англ.] / Л. Бриллюэн – М.: Государственное издательство физико-математической литературы, 1960.
