ТЕОРИЯ K+/ Na+ СЕЛЕКТИВНОСТИ ВОДНОЙ ПОЛОСТИ В K+ КАНАЛЕ ДЛЯ ПОЛЮСНЫХ МОДЕЛЕЙ ДИЭЛЕКТРИЧЕСКОЙ ФУНКЦИИ РАСТВОРИТЕЛЯ

Рубашкин А.А.¹, Цыганов А. Б.², Воротынцев М. А.³

¹ORCID: 0000-0002-9054-0574, Кандидат химических наук, Институт цитологии РАН, Санкт-Петербург, ²ORCID: 0000-0003-2245-3097, Кандидат физико-математических наук, ООО «Интро-Микро», Санкт-Петербург, ³ORCID: 0000-0002-0720-4300, Доктор физико-математических наук, МГУ им. М.В. Ломоносова, Москва

Работа выполнена при поддержке гранта РФФИ № 14-03-00221

ТЕОРИЯ K+/ Na+ СЕЛЕКТИВНОСТИ ВОДНОЙ ПОЛОСТИ В K+ КАНАЛЕ ДЛЯ ПОЛЮСНЫХ МОДЕЛЕЙ ДИЭЛЕКТРИЧЕСКОЙ ФУНКЦИИ РАСТВОРИТЕЛЯ

Аннотация

В статье рассмотрено применение нелокально-электростатической теории сольватации ионов к расчету K⁺/Na⁺ селективности в центральной полости, находящейся в центре K⁺ канала. Показано, что при увеличении корреляционной длины воды в полости в три раза по сравнению с ее значением в свободном растворе величина K⁺/Na⁺ селективности равна двум для расчета по двухполюсной модели диэлектрической функции растворителя. С учетом разницы концентраций K⁺ и Na⁺ внутри клетки из этого следует, что доля K⁺ каналов, в полости которых проникают катионы Na⁺, по крайней мере на порядок меньше, чем количество каналов, свободных для транспорта K⁺.

Ключевые слова: энергия сольватации, ионный обмен, нелокальная электростатика.

Rubashkin A.A.¹, Tsyganov A. B.², Vorotyntsev M. A.³

¹ORCID: 0000-0002-9054-0574, PhD in Chemistry, Institute of Cytology, Russian Academy of Sciences, Saint-Petersburg, ²ORCID: 0000-0003-2245-3097, PhD in Physics and Mathematics, Intro-Micro LLC, Saint-Petersburg,³ORCID: 0000-0002-0720-4300, PhD in Physics and Mathematics, Lomonosov Moscow State University, Moscow

THEORY OF K+/ Na+ SELECTIVITY IN WATER CAVITY OF K+ CHANNEL FOR THE POLE MODELS OF DIELECTRIC FUNCTIONS OF THE SOLVENT

Abstract

The article considers the use of nonlocal-electrostatic theory of ion solvation to the calculation of K⁺/Na⁺ selectivity in the central cavity of K⁺ channel. It is shown that by increasing the correlation length of the water in the cavity is three times as compared with its value in free solution the magnitude of K⁺/Na⁺ selectivity is two for the calculation on the two-pole model of the dielectric function of the solvent. Considering the difference of concentrations K⁺ and Na⁺ inside the cell follows from this, that the proportion of K⁺ channels, in the cavity of which penetrate the cations Na⁺, at least an order of magnitude smaller than the number of channels available for the transport of K⁺.

Keywords: solvation energy, ion exchange, nonlocal electrostatics. Селективность центральной полости в K⁺ канале.

В работе [1], выполненной в лаборатории Р. Маккиннона (R. MacKinnon) и за которую в 2003 г. он получил нобелевскую премию по химии, было экспериментально доказано существование центральной водной полости в середине бактериального Kcsa K⁺ канала. Эта работа обсуждалась в известной монографии Хилле [2], а существование водной полости в K⁺ каналах другого типа было показано в [3].

В [4-6] применялись теоретические методы для моделирования водной полости K⁺ канала. Так в [4] Маккиннон с соавтором применил методы молекулярной динамики и классической электростатики для моделирования процесса стабилизации катиона K⁺ в этой полости, а в [5-6] использовались методы квантовой механики для анализа селективности полости.

Величина K⁺/Na⁺ селективности K⁺ канала определяется селективным фильтром [1-3], однако водная полость канала также должна обладать некоторой K⁺/Na⁺ селективностью, хотя и значительно меньшей, чем его селективный фильтр. В противном случае значительная часть центральных полостей K⁺ каналов были бы заполнены катионами Na⁺, которые не могли бы двигаться дальше через канал из-за того, что селективный фильтр K⁺ канала не пропускал бы их. В этом случае катионы Na⁺ в полости находились бы в состоянии ион обменного равновесия с раствором, а катионы K⁺ не смогли бы проходить через такие каналы из-за электростатического отталкивания с катионами Na⁺.

В настоящей работе проведено изучение K⁺/Na⁺ селективности полости методами нелокальной электростатики [7-8], при этом использовались полюсные [9-10] модели диэлектрической функции растворителя.

Расчет энергии сольватации ионов методами нелокальной электростатики.

Энергия сольватации W иона в свободном растворе будет вычисляться по формулам нелокально-электростатической теории [9-10] для случая, когда заряд иона имеет сферически-симметричное распределение и находится на борновской сфере радиуса, равному радиусу иона r_i.

Приведем формулы для моделей нелокального диэлектрического отклика растворителя (заполняющего все пространство) ε(k), на которые будем ссылаться в дальнейшем изложении. В литературе эти модели называются ”приближениями нескольких (1, 2 или 3) дискретных мод” или “полюсными моделями” [8]. В этих формулах k - волновой вектор, ε₁, ε₂, ε₃ - диэлектрические проницаемости, а λ₁, λ₂, λ₃ - корреляционные длины, соответствующие электронным (индекс 1), инфракрасным (индекс 2) и дебаевским (индекс 3) степеням свободы. Согласно [8] численные значения диэлектрических проницаемостей для воды: ε₁ = 1.8, ε₂ = 5, ε₃ = ε_S = 78 (ε_S - статическая диэлектрическая проницаемость воды), а корреляционных длин: λ₁ = 0.5 Å, λ₂ = 1 Å, а величина наибольшей из корреляционных длин λ₃ (λ₃ = Λ_o - корреляционная длина в цепочках водородной связи, где Λ_o – ее значение в свободном растворе) используется в качестве подгоночного параметра, который для свободного раствора принимается равным: Λ_o = 3 Å.

В трёхполюсной модели ε(k) имеет вид:

        (1)

Поскольку λ₁ мало, то в знаменателе второго члена в правой части (1) 1 >> (kλ₁)² для интервала значений k, дающих основной вклад в энергию сольватации. При этом модель (1) переходит в двухполюсную модель [9], в которой ε(k) имеет вид:

        (2)

Приведем формулы для энергий сольватации в теории Корнышева [8-10] для модели, когда заряд иона равномерно распределен по поверхности сферы радиуса, совпадающего с радиусом иона (борновская модель иона). Энергия выражается через вспомогательную функцию f(y):

     (3) В двухполюсной модели [9] энергия сольватации W_o зависит от радиуса иона r_i: ,    (4)

где e - заряд электрона, r_i – радиус иона. Коэффициенты C_i (i = 1,2,3) определяются через диэлектрические константы:

. Для качественных оценок часто используется однополюсная модель ε(k) [10], которая получается пренебрежением дисперсии диэлектрического отклика в промежуточном интервале длин волн: ε₂ = ε₁. Тогда формула (2) переходит в формулу:        (5)

Для однополюсной модели [10] энергия сольватации W_o рассчитывается по следующей формуле, в которой функция f(y) определяется формулой (3).

.     (6)

Расчет изменения энергии сольватации при переходе катионов K⁺ и Na⁺ из свободного раствора в центральную полость K⁺ канала. Ионный обмен между раствором и полостью.

В этом разделе нелокально-электростатическая теория ионной сольватации [7-10] применяется к моделированию ионного обмена K⁺ и Na⁺ между раствором и полостью, окруженной белковым веществом. Наш подход к этому явлению основывается на предположении о том, что этот процесс определяется изменением энергии сольватации ионов δW при их переходе из свободного раствора в полость. В соответствии с нелокальной электростатикой энергия δW зависит как от радиусов ионов, так и от параметров воды в полости (корреляционных длин, коротковолновой и статической диэлектрических проницаемостей). Согласно [11], корреляционная длина воды в окрестности белков значительно превышает ее значение Λ_o в объёме раствора. Для полости это приводит к тому, что величина δW отличается от нуля, и как следствие к возникновению K⁺/Na⁺ селективности в ней.

Энергия K⁺ и Na⁺ в полости состоит из трех слагаемых. Первые из этих слагаемых δW_K⁺ и δW_Na⁺ определяются энергией пересольватации K⁺ и Na⁺ из-за перехода этих катионов в среду с другими параметрами, поскольку корреляционная длина воды в полости Λ_{Cav ­}(нижний индекс ‘Cav’ от английского ‘cavity’) превышает ее значение в свободном растворе Λ_o. Второе слагаемое W_im обусловлено ролью спиральных фрагментов белковых молекул, ограничивающих центральную полость канала [1-4]. Роль этого эффекта в изменении энергии иона при его переходе в полость для случая сферической полости была изучена нами в [12].  Вторые слагаемые W_im(K⁺) и W_im(Nа⁺) для K⁺ и Na⁺ в полости можно считать одинаковыми из-за того, что разница радиусов K⁺ и Na⁺ значительно меньше размеров центральной полости K⁺ канала. Третьи слагаемые - электростатическое взаимодействие ионов в полости с заряженными группами белков, окружающих полость: eφ­_Cav, где φ­_Cav – электростатический потенциал в полости.

При расчете S_K⁺_/Na⁺ - величины K⁺/Na⁺ селективности полости по формуле (7) сомножители, содержащие exp(W_im), как и сомножители exp(eφ­_Cav), сокращаются, и ее величина определяется только энергиями δW_K и δW_Na:

 (7)

При выводе формулы (7) мы использовали равенство электрохимических потенциалов ионов в полости и в свободном растворе, нашли их концентрации в полости, а K⁺/Na⁺ селективность полости определили, как отношение концентрации K⁺ в полости к концентрации Na⁺.

Энергия сольватации W_Cav в полости зависит от радиуса иона и от корреляционной длины Λ_Cav воды в полости. Формула (4), по которой энергия сольватации рассчитывалась для двухполюсной модели ε(k) при λ₃ = Λ_o, для иона в полости (λ₃ = Λ_Cav) имеет вид:

,      (8) а для случая однополюсной модели ε(k) формула (6) для W_Cav переходит в: .      (9) Разница энергии сольватации иона δW между её значением в свободным растворе и водной полости канала: .       (10) Пользуясь формулой (10), определим энергии пересольватации Na⁺ и Cl^- с помощью соотношений:        (11) Селективность в полости определяется формулой (12), которая следует из формулы (7): .     (12) Результаты расчета K⁺/ Na⁺ селективности водной полости. На Рис. 1 представлены результаты расчета K⁺/Na⁺ селективности водной полости, окруженной белками.  

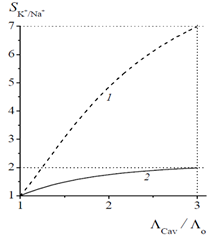
Рис. 1 – K⁺/Na⁺ селективность в водной полости S_K⁺_/Na⁺ в зависимости от корреляционной длины Λ_Cav в полости

 

По оси ординат: S_K⁺_/Na⁺ рассчитанная по формуле (12). По оси абсцисс: отношение корреляционной длины воды Λ_Cav в полости к Λ_o – значению корреляционной длины в свободном растворе, равному 3 Å. Штриховая кривая 1 рассчитана для однополюсной модели ε(k), а сплошная кривая 2 - для двухполюсной модели ε(k). Радиусы Na⁺ и K⁺ взяты по шкале Гурари и Адриана [13]: r_Na⁺ = 1.17 Å, r_K⁺ = 1.49 Å.

Выводы из расчетов K⁺/Na⁺ селективности полости.

При увеличении корреляционной длины воды в полости в 3 раза величина S_K⁺_/Na⁺ увеличивается в два раза для расчета, выполненного для двухполюсной модели ε(k), и в семь раз для однополюсной модели. Отметим, что согласно [8, 9] расчет изменения энергии сольватации ионов по двухполюсной модели ε(k) более точен, чем по однополюсной.

Главный вывод заключается в том, что водная полость в белковом окружении обладает K⁺/Na⁺ селективностью для обеих моделей диэлектрической функции. Из этого следует, что центральная полость в K⁺ канале будет преимущественно пропускать катионы K⁺, даже если концентрации K⁺ и Na⁺ в клетке сравнимы. В реальности концентрация K⁺ во внутриклеточной среде в несколько раз превосходит концентрацию Na⁺. Учитывая полученные результаты по селективности, из этого следует, что доля K⁺ каналов, в полости которых проникают катионы Na⁺, по крайней мере на порядок меньше, чем количество каналов, свободных для K⁺.

Литература

1. DoyleDA, Morais Cabral J, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, Chait BT, MacKinnonR. The structure of the potassium channel: molecular basis of K+ conduction and selectivity // Science. – 1998. - V. 280. - № 5360. – P. 69-77.
2. Hille B. Ion channels of excitable membrane. (3rd ed.) Sunderland, Massachusetts U.S.A.: Sinauer Associates, Inc., 2001. 814 p.
3. Hite R. K., Yuan P., Li Z., Hsuing Y., Walz T., MacKinnon R. Cryo-electron microscopy structure of the Slo 2.2 Na⁺ - activated K⁺ channel // Nature. – 2015. - V. 527. - № 7577. – P. 198-203.
4. Roux B., MacKinnon R. The cavity and pore helices in the KcsA K+ channel: electrostatic stabilization of monovalent cations // Science. – 1999. - V. 285. - № 5424. – P. 100-102.
5. KarievA., Green M. E. Quantum calculations on water in the KcsA channel cavitywith permeant and non-permeant ions. // Biochim. Biophys. Acta. – 2009. - V. 1788. - № 5 – P. 1188-1192.
6. KarievA. M., Green M. E. Quantum mechanical calculations on selectivity in the KcsA channel: the role of the aqueous cavity // J. Phys. Chem. B. – 2008. - V. 112. № 4. – P. 1293-1298.
7. Dogonadze R., Kornyshev A. A. Polar-solvent structure in theory of ionic solvation // J. Chem. Soc. Faraday Trans. Pt.II. – 1974. - V. 70. – P. 1121-1132.
8. Воротынцев М. А., Корнышев А. А. Электростатика сред с пространственной дисперсией. М.: Наука, 1993. С. 20-35.
9. Kornyshev A. A., Volkov A.G. On the evaluation of standard Gibbs energies of ion transfer between 2 solvents // J. Electroanal. Chem. – 1984. - V. 180. – P. 363-381.
10. Kornyshev A. A. Nonlocal screening of ions in a structurized polar liquid - new aspects of solvent description in electrolyte theory // Electrochim Acta. – 1981. - V. 26. – P. 1-20.
11. Ebbinghaus S., Kim S. J., Heyden M., Yu X., Heugen U., Gruebele M., Leitner D. M., Havenith M. An extended dynamical hydration shell around proteins. // Proc. Natl. Acad. Sci. USA. – 2007. - V. 104. – P. 20749 -20752.
12. Рубашкин А. А. Роль пространственной дисперсии диэлектрической проницаемости сферической водной полости в уменьшении свободной энергии переноса иона в полость // Электрохимия. – 2014. - Т. 50. - № 11. – С. 1212-1217.
13. Gourary B. S., Adrian F. J. Wave Function for Electron-Excess Color Centers in Alkali Halide Crystals // Solid State Phys. – 1960. - V. 10. – P. 127-247.

 References

1. DoyleDA, Morais Cabral J, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, Chait BT, MacKinnonR. The structure of the potassium channel: molecular basis of K+ conduction and selectivity // Science. – 1998. - V. 280. - № 5360. – P. 69-77.
2. Hille B. Ion channels of excitable membrane. (3rd ed.) Sunderland, Massachusetts U.S.A.: Sinauer Associates, Inc., 2001. 814 p.
3. Hite R. K., Yuan P., Li Z., Hsuing Y., Walz T., MacKinnon R. Cryo-electron microscopy structure of the Slo 2.2 Na⁺ - activated K⁺ channel // Nature. – 2015. - V. 527. - № 7577. – P. 198-203.
4. Roux B., MacKinnon R. The cavity and pore helices in the KcsA K+ channel: electrostatic stabilization of monovalent cations // Science. – 1999. - V. 285. - № 5424. – P. 100-102.
5. KarievA., Green M. E. Quantum calculations on water in the KcsA channel cavitywith permeant and non-permeant ions. // Biochim. Biophys. Acta. – 2009. - V. 1788. - № 5 – P. 1188-1192.
6. KarievA. M., Green M. E. Quantum mechanical calculations on selectivity in the KcsA channel: the role of the aqueous cavity // J. Phys. Chem. B. – 2008. - V. 112. № 4. – P. 1293-1298.
7. Dogonadze R., Kornyshev A. A. Polar-solvent structure in theory of ionic solvation // J. Chem. Soc. Faraday Trans. Pt.II. – 1974. - V. 70. – P. 1121-1132.
8. Vorotyntsev M. A., Kornyshev A. A. Elektrostatika sred s prostranstvennoj dispersiej. M.: Nauka, 1993. S. 20-35.
9. Kornyshev A. A., Volkov A. G. On the evaluation of standard Gibbs energies of ion transfer between 2 solvents // J. Electroanal. Chem. – 1984. - V. 180. – P. 363-381.
10. Kornyshev A. A. Nonlocal screening of ions in a structurized polar liquid - new aspects of solvent description in electrolyte theory // Electrochim Acta. – 1981. - V. 26. – P. 1-20.
11. Ebbinghaus S., Kim S. J., Heyden M., Yu X., Heugen U., Gruebele M., Leitner D. M., Havenith M. An extended dynamical hydration shell around proteins. // Proc. Natl. Acad. Sci. USA. – 2007. - V. 104. – P. 20749 -20752.
12. Rubashkin A. A. The role of spatial dispersion of the dielectric constant of spherical water cavity in the lowering of the free energy of ion transfer to the cavity // Russ. J. Electrochem. – 2014. - Т. 50. - № 11. – P. 1090-1094.
13. Gourary B. S., Adrian F. J. Wave Function for Electron-Excess Color Centers in Alkali Halide Crystals // Solid State Phys. – 1960. - V. 10. – P. 127-247.