МОДЕЛИРОВАНИЕ ПРОЦЕССА ИНДУКЦИОННОГО НАГРЕВА ПЛАЗМЕННО-НАПЫЛЕННЫХ ИЗНОСОСТОЙКИХ ПОКРЫТИЙ

Скиба В.Ю.¹, Зверев Е.А.², Вахрушев Н.В.³, Гаврилов А.К.⁴

¹ORCID: 0000-0002-8242-2295, Кандидат технических наук, доцент, ²ORCID: 0000-0003-4405-6623, Кандидат технических наук, ³ORCID: 0000-0002-2273-5329, Аспирант, ⁴Студент, Новосибирский государственный технический университет

Работа выполнена при финансовой поддержке в рамках Тематического плана НИР НГТУ по проекту  ТП-ПТМ-2_15 в плановом периоде 2015-2016 гг.

МОДЕЛИРОВАНИЕ ПРОЦЕССА ИНДУКЦИОННОГО НАГРЕВА ПЛАЗМЕННО-НАПЫЛЕННЫХ ИЗНОСОСТОЙКИХ ПОКРЫТИЙ

Аннотация

В работе представлены результаты моделирования процесса индукционного нагрева токами высокой частоты при оплавлении плазменного покрытия. Задача определения остаточных напряжений в покрытии решена методом конечных элементов с использованием программных комплексов ANSYS и SYSWELD. Проверка результатов численного моделирования осуществлялась посредством экспериментального определения остаточных напряжений. В оплавленном плазменном покрытии формируются сжимающие остаточные напряжения, а так же наблюдается уменьшение пористости и более равномерное распределение микротвердости, что способствует повышению надежности деталей машин.

Ключевые слова: плазменное напыление, индукционный нагрев ТВЧ, оплавление, поверхностный слой, конечно-элементное моделирование.

 Skeeba V.Yu.¹, Zverev E.A.², Vakhrushev N.V.³, Gavrilov A.K.⁴

¹ORCID: 0000-0002-8242-2295, PhD in Engineering, Associate professor; ²ORCID: 0000-0003-4405-6623, PhD in Engineering; ³ORCID: 0000-0002-2273-5329, Postgraduate student; ⁴Student, Novosibirsk State Technical University

This study was supported by a NSTU grant (project No. ТП-ПТМ-2_15)

SIMULATION OF THE INDUCTION HEATING PROCESS OF WEAR-RESISTANT PLASMA COATINGS

Abstract

The simulation results of process of high-frequency induction heating at melting plasma coating are presented in this paper. The problem of determining the residual stress in the coating is solved by the finite element method with the use of ANSYS and SYSWELD software systems. The numerical simulations results were checked by experimental measurement of residual stresses. Formation of compressive residual stresses as well as porosity reduction and more uniform distribution of microhardness are observed in the melted plasma coating, thereby increasing the reliability of machine parts.

Keywords: plasma spraying, induction heating HFC, melting, surface layer, finite-element modeling.

Проблему повышения надежности выпускаемых изделий невозможно решить без разработки и совершенствования современных технологий поверхностного упрочнения. Среди наиболее распространенных в промышленности методов поверхностного упрочнения деталей особое место занимает процесс плазменного напыления износостойких покрытий [1]. Несмотря на ряд очевидных достоинств, которые присущи данному методу, ему свойственны и недостатки, обусловленные нестабильностью показателей качества напыленного слоя: степени расплавленности порошкового материала, количества и размера пор, а также характера границы между покрытием и основой. Эти показатели закономерно предопределяют адгезионную прочность покрытий, знак и величину остаточных напряжений в слое покрытия. Так, относительно невысокий уровень адгезионной прочности при высоких контактных давлениях может являться причиной нарушения сплошности поверхности плазменных покрытий в виде отслоений и сколов частиц покрытия в процессе эксплуатации оборудования, что, естественно, ограничивает его технический ресурс.

Для увеличения адгезионной прочности, уменьшения пористости, ликвидации нерасплавленных частиц порошка в структуре покрытий и обеспечения равномерного распределения микротвердости по глубине упрочненного слоя используют повторное оплавление покрытия концентрированными источниками энергии [2, 3].

Анализ технологических возможностей основных методов обработки концентрированными источниками энергии (электродуговой, электронно-лучевой, лазерный, плазменный и индукционный), которые можно использовать для повторного высокоэнергетического воздействия на структуру плазменных покрытий, показал, что при повторной обработке токопроводящих плазменных покрытий явным преимуществом обладает высокоэнергетический нагрев токами высокой частоты (ТВЧ) [4]. Характерной особенностью этого процесса является то, что источник нагрева является объемным и выделение энергии осуществляется в поверхностном слое, толщина которого определяется частотой тока, удельным электрическим сопротивлением и теплофизическими характеристиками материала покрытия. Выбор соответствующей частоты генератора позволяет осуществлять одновременный нагрев во всей толщине нанесенного покрытия.

При данной технологии сложной задачей является обеспечение качества оплавленных покрытий.  Основной проблемой является определение области рациональных режимов обработки. Необходимо учитывать, что чрезмерный нагрев приводит к изменению химического и фазового составов, к росту остаточных напряжений и, следовательно, к снижению работоспособности покрытий. Для решения данной проблемы целесообразным является применение математического моделирования.

Целью работы является разработка математической модели индукционного нагрева ТВЧ при оплавлении покрытия и сопоставление результатов численного моделирования с данными экспериментальных исследований.

Методика экспериментального исследования.

Покрытия наносили методом плазменного напыления на пластины размером 100х10х10 мм, изготовленные из стали 20. С целью активации поверхности образцы подвергались струйно-абразивной очистке частицами электрокорунда марки 13А (до шероховатости Rz = 50…75 мкм) [3].

В качестве материала для напыления покрытия использовали порошок хромистого чугуна марки ПГ-С27 (с фракционным размером 50…100 мкм). Напыление производилась на установке "Киев-7" плазмотроном ПУН-8 мощностью 40 кВт. Режимы напыления: сила тока дуги I = 140 А; напряжение U = 140 В; расход плазмообразующего газа (воздуха) G = 18 л/мин, при давлении P = 0,4 МПа; дистанция напыления L = 110 мм; скорость перемещения плазмотрона V = 12 м/мин [1].

Оплавление поверхности образцов осуществлялось на экспериментальной установке с плавным регулированием скорости. Источником энергии служил генератор марки ВЧГ 6-60/0.44 с рабочей частотой тока 440∙10³ Гц. Процесс нагрева осуществлялся по глубинной схеме (глубина выделения энергии 0,6…0,8 мм) непрерывно-последовательным способом. Использовался индуктор петлевого типа, оснащенный ферритовым магнитопроводом марки N87 с магнитной проницаемостью m_i = 2200 [5]. Коэффициент теплоотдачи при охлаждении на воздухе - a = 3∙10³ Вт/(м²∙^оС). Удельная мощность нагрева варьировалась в пределах q_и = (2,8…3,4)∙10⁸ Вт/м², а скорость перемещения детали V_д = 20…120 мм/с. Ширина активного провода индуктора составляла R_и = 2 мм, обработка осуществлялась с зазором Δ = 0,1…0,2 мм.

Определение пористости покрытия осуществлялось металлографическим методом [4]. Исследования структуры выполнялось на световом микроскопе NIKON Eclipse MA100. Микротвердость (HV) покрытий определялась на приборе Wolpert Group 402MVD. Исследование остаточных напряжений проводилось методом электролитического травления [5].

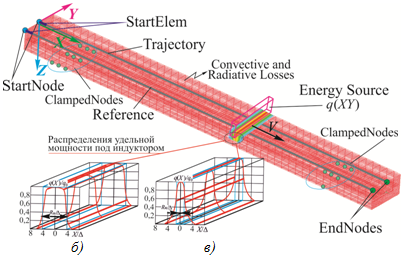
Математическое моделирование.

Создание расчетной модели осуществлялось в комплексе ANSYS. Генератором была сформирована гексаэдрическая КЭ сетка с использованием следующих типов конечных элементов: Solid bodies – твердые тела моделировались 8-узловыми тетраэдрами SOLID 45; Surface bodies поверхностные тела моделировались 4-узловыми 4-угольными оболочковыми элементами – SHELL 63; Line bodies – линейные тела моделировались 2-узловыми линейными элементами LINK 8. Размер конечных элементов составлял 0,01…1 мм. Общее количество элементов (Elements) – 74800 (рис. 1, а).

Рис. 1 - Конечно-элементная модель образца и характер распределения удельной мощности под индуктором: q_o – максимальное значение удельной мощности; b – ширина паза магнитопровода (1,2…2 мм); D – величина зазора между индуктором и деталью (0,1…0,8 мм). а) – КЭМ; б) –  b/Δ  = 10; в) –  b/Δ  = 1

При создании КЭ модели были созданы следующие компоненты: «Volume» - группа трехмерных элементов, обозначающих обрабатываемый объект; «Trajectory» - группа одномерных элементов, которая определяет траекторию перемещения источника энергии высокой концентрации; «Reference» - опорная эквидистанта – группа одномерных элементов, способствующая ориентированию локальной системы координат источника энергии; «StartElem» - стартовые элементы начала действия источника; «StartNodes» и «EndNodes» - начальные и конечные узлы на траектории перемещения; «Skin» - группа двухмерных элементов, обозначающие поверхности, по которым происходит конвективные и радиационные тепловые потери (Convective and Radiative Losses); «ClampedNodes» - группа узлов, по которым происходит закрепление пластины.

Моделирование процесса ТВЧ осуществлялось в системе SYSWELD, позволяющей производить расчеты температурных полей, распределения твердости, внутренних напряжений и деформаций.

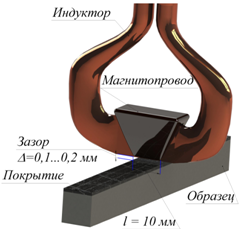
Для того чтобы воспользоваться математическим аппаратом теории теплопроводности, необходимо описание теплового источника в месте его действия. При обработке ТВЧ форма источника в плоскости X-Y представляет собой прямоугольник, стороны которого определяются длиной l и шириной паза магнитопровода b (рис. 2).

Рис. 2 - Общий вид зоны обработки

 

Распространение индуктивного тока на поверхности обрабатываемого изделия будет определять распределение удельной мощности. Вдоль оси Y распределение удельной мощности равномерно, а по оси X - определяется отношением ширины паза магнитопровода b к величине зазора Δ между обрабатываемой деталью и активным проводом индуктора. Кривые распределения удельной мощности представлены на рисунке 1 б и 1 в. Здесь отношение  , где q(X), q₀, H_X, H₀ – значения удельной мощности и напряженности магнитного поля на поверхности.

Принимая во внимание результаты работ [6, 7], можно отметить стадийный характер процесса перераспределения выделяемой энергии по глубине материала при индукционном нагреве ТВЧ. Распределение мощности по глубине материала описывается зависимостью      (1)

где q₀ – мощность, выделяемая в поверхностном слое; ρ_э  и  - удельное электрическое сопротивление и относительная магнитная проницаемость материала соответственно.

Выделение энергии происходит послойно, глубина проникновения тока будет увеличиваться до тех пор, пока вся подводимая энергия не будет поглощена горячим слоем, потерявшим ферромагнитные свойства. Поэтому по мере расширения зоны, в которой материал теряет свои магнитные свойства, будет наблюдаться и постепенное уменьшение уровня удельной мощности, связанное с изменением значений параметров r_э и m. В значительной степени максимальная глубина проникновения тока зависит от частоты.

Специфика перераспределения выделяемой энергии по глубине материала была учтена в процессе формирования параметров конечно-элементной модели. Необходимые зависимости теплофизических и физико-механических характеристик принимались согласно данным, представленным в работе [7].

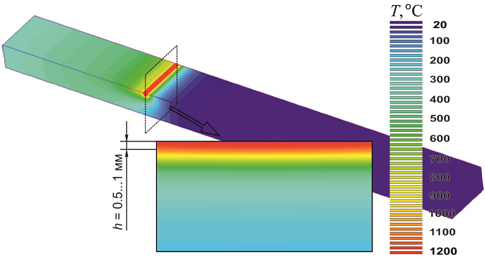
Результаты и обсуждение.

В результате численного моделирования были получены распределения тепловых полей в процессе оплавления плазменного покрытия. Как видно из рисунка 3, температура на поверхности детали, на глубине равной толщине покрытия (h = 0.5~1 мм) достигает значений порядка 1200 ^oС (температуры плавления порошка марки ПГ-С27).

Рис. 3 - Распределение тепловых полей в процессе оплавления ТВЧ: q_ист = 3,4·10⁸ Вт/м², V_ист = 100 мм/с

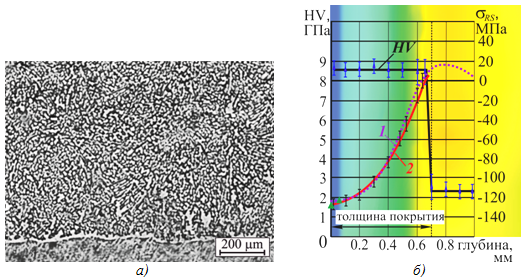
Результаты металлографического анализа оплавленных покрытий показывают, что в структуре практически ликвидируются поры и нерасплавленные частицы порошка, отсутствуют участки с несплошностью на переходной границе (рис. 4 а). Исследование динамики процесса позволило определить скорости нагрева (охлаждения), которые достигают следующих значений: V_Н = 5200 ^oC/с, V_О = -2800 ^oC/с.

На рисунке 4 б представлено поле распределения остаточных напряжений (осевых). Уровень s_сж на поверхности достигает значений -120…-130 МПа, причем пик растягивающих напряжений смещен на глубину порядка 0,8…1,2 мм.

Таким образом, средствами конечно-элементных комплексов ANSYS и SYSWELD с учетом характерных особенностей распределения тепловой энергии при индукционном нагреве разработана математическая модель оплавления покрытия. Получены значения температурных полей и скоростей нагрева-охлаждения.

Рис. 4 - Качественные показатели плазменного покрытия после оплавления ТВЧ: а) структура оплавленного плазменного покрытия; б) распределение микротвердости по глубине слоя на фоне остаточных напряжений: 1 - расчетная эпюра осевых остаточных напряжений; 2 - эпюра остаточных напряжений, полученная экспериментально

При нагреве ТВЧ в покрытии формируются остаточные напряжения сжатия, уровень которых составляет порядка -120…-130 МПа, наблюдается уменьшение пористости с 12 % до 1 % и повышение равномерности распределения микротвердости по глубине слоя. Использование конечно-элементной модели позволит определить рациональные режимы при оплавлении плазменных покрытий посредством индукционного нагрева ТВЧ.

Литература

1. Чёсов Ю.С., Зверев Е.А. Методика нанесения плазменных износостойких покрытий // Научный вестник НГТУ. 2014. № 2(55). С. 156-165.
2. Структурные особенности износостойких плазменных покрытий после воздействия токами высокой частоты / Е.А. Зверев, Ю.С. Чёсов, Н.В. Вахрушев, П.В. Трегубчак, Д.Ю. Зарубин // Актуальные проблемы в машиностроении. 2015. № 2. С. 347-353.
3. Чесов Ю.С., Зверев Е.А. Качество износостойких плазменных покрытий после индукционного нагрева // В мире научных открытий. 2015. № 2(62). С. 248-266.
4. Структура износостойких плазменных покрытий после высокоэнергетического воздействия ТВЧ / Ю.С. Чёсов, Е.А. Зверев, В.В. Иванцивский, В.Ю. Скиба, Н.В. Плотникова, Д.В. Лобанов // Обработка металлов (технология, оборудование, инструменты). 2014. № 4 (65). С. 11-18.
5. Анализ напряженно-деформированного состояния материала при высокоэнергетическом нагреве токами высокой частоты / В.Ю. Скиба, В.Н. Пушнин, И.А. Ерохин, Д.Ю. Корнев // Обработка металлов (технология, оборудование, инструменты). 2014. № 3 (64). С. 90–102.
6. Моделирование напряженно-деформированного состояния материала в программном комплексе SYSWELD при поверхностной закалке ТВЧ / В. Ю. Скиба, В. Е. Воротников, Р. А. Гарин, Е. А. Гарин // В мире научных открытий. 2010. №2-3. С. 16-19.
7. Иванцивский В.В., Батаев В.А. Упрочнение поверхностных слоев деталей машин с использованием высокоэнергетического нагрева токами высокой частоты // Ползуновский вестник. 2005. № 2-2. С. 104–112.

References

1. Chjosov Ju.S., Zverev E.A. Metodika nanesenija plazmennyh iznosostojkih pokrytij // Nauchnyj vestnik NGTU. 2014. № 2(55). S. 156-165.
2. Strukturnye osobennosti iznosostojkih plazmennyh pokrytij posle vozdejstvija tokami vysokoj chastoty / E.A. Zverev, Ju.S. Chjosov, N.V. Vahrushev, P.V. Tregubchak, D.Ju. Zarubin // Aktual'nye problemy v mashinostroenii. 2015. № 2. S. 347-353.
3. Chesov Ju.S., Zverev E.A. Kachestvo iznosostojkih plazmennyh pokrytij posle indukcionnogo nagreva // V mire nauchnyh otkrytij. 2015. № 2(62). S. 248-266.
4. Struktura iznosostojkih plazmennyh pokrytij posle vysokojenergeticheskogo vozdejstvija TVCh / Ju.S. Chjosov, E.A. Zverev, V.V. Ivancivskij, V.Ju. Skiba, N.V. Plotnikova, D.V. Lobanov // Obrabotka metallov (tehnologija, oborudovanie, instrumenty). 2014. № 4 (65). S. 11-18.
5. Analiz naprjazhenno-deformirovannogo sostojanija materiala pri vysokojenergeticheskom nagreve tokami vysokoj chastoty / V.Ju. Skiba, V.N. Pushnin, I.A. Erohin, D.Ju. Kornev // Obrabotka metallov (tehnologija, oborudovanie, instrumenty). 2014. № 3 (64). S. 90–102.
6. Modelirovanie naprjazhenno-deformirovannogo sostojanija materiala v programmnom komplekse SYSWELD pri poverhnostnoj zakalke TVCh / V. Ju. Skiba, V. E. Vorotnikov, R. A. Garin, E. A. Garin // V mire nauchnyh otkrytij. 2010. №2-3. S. 16-19.
7. Ivancivskij V.V., Bataev V.A. Uprochnenie poverhnostnyh sloev detalej mashin s ispol'zovaniem vysokojenergeticheskogo nagreva tokami vysokoj chastoty // Polzunovskij vestnik. 2005. № 2-2. S. 104–112.