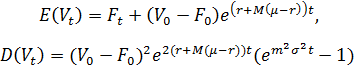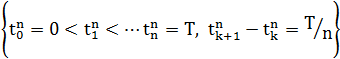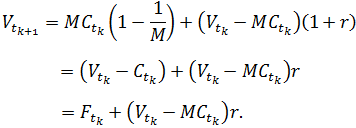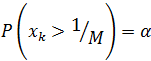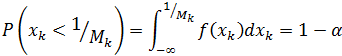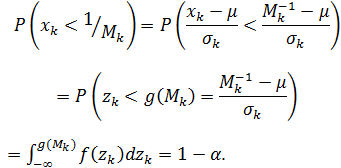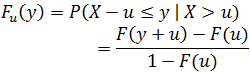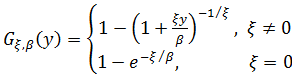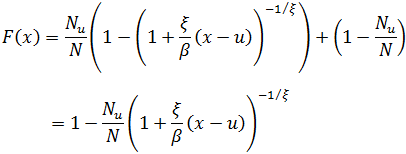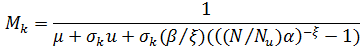ЗАЩИТА СТРАТЕГИИ ПОРТФЕЛЬНОГО УПРАВЛЕНИЯ С ДИНАМИЧЕСКОЙ РЕБАЛАНСИРОВКОЙ АКТИВОВ ОТ РИСКА ИЗБЫТОЧНЫХ ПОТЕРЬ

Научная статья

Ткач Тимофей Сергеевич

Выпуск: № 6 (37), 2015

Опубликована:

2015/07/15

PDF

Ткач Тимофей Сергеевич

Студент магистратуры, НИУ ВШЭ

ЗАЩИТА СТРАТЕГИИ ПОРТФЕЛЬНОГО УПРАВЛЕНИЯ С ДИНАМИЧЕСКОЙ РЕБАЛАНСИРОВКОЙ АКТИВОВ ОТ РИСКА ИЗБЫТОЧНЫХ ПОТЕРЬ

Аннотация

Работа посвящена крайне актуальной, но пока недостаточно широко используемой в России практике портфельного управления на основе стратегии с динамической ребалансировкой активов. В начале статьи описываются основные принципы ее работы, затем автором предлагается модель, учитывающая изменения параметров рыночной волатильности и риска, которая призвана минимизировать риски чрезвычайных потерь

Ключевые слова: стратегия, динамическая ребалансировка активов, управление портфелем, риски, инвестиции

Timofey Tkach

Graduate student, Research University The Higher School of Economics

GAP RISK MANAGEMENT OF THE CPPI STRATEGY

Annotation

The article provides basics and main characteristics of CPPI portfolio strategy and focuses on the main risk managing problem. Using dynamic multiple setting approach was created special model, which could allow portfolio managers and investors to choose appropriate multiple and risk exposure level.

Keywords: CPPI, portfolio strategy, portfolio management, risk, investment

Constant proportion portfolio insurance – это одна из популярных стратегий, использующая динамическую ребалансировку активов, она позволяет обеспечить сохранение стоимости капитала к определенному моменту времени в будущем.

Изначально стратегия CPPI была разработана для крупных частных инвесторов, но впоследствии получила распространение и у частных фондов и страховых компаний [1,2].

В основе стратегии лежит формирование портфеля из безрисковых и рискованных финансовых инструментов, соотношение долей которых в портфеле меняется со временем.

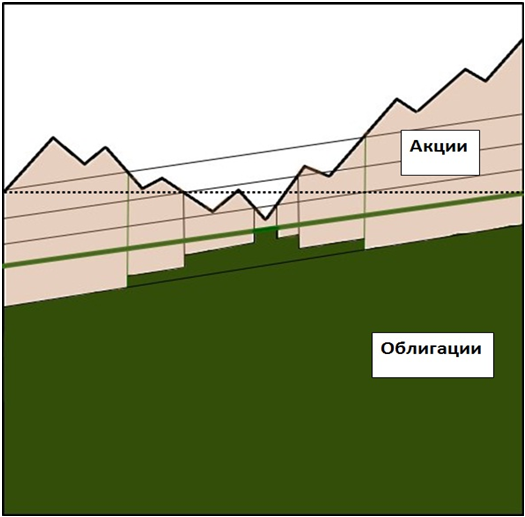
К безрисковым активам, пригодным для реализации стратегии, можно отнести государственные или надежные корпоративные облигации с высоким кредитным рейтингом. К рискованным же активам можно отнести ликвидные акции, по которым ожидается рост в течение срока инвестирования, либо фьючерсы на фондовый индекс.

Перераспределение долей в портфеле между акциями и облигациями происходит в зависимости от динамики рынка при заданных параметрах доходности и сроках инвестиций.

В случае устойчивого роста рынка, доля рискованных активов увеличивается, позволяя инвестору не оставаться в стороне от положительного тренда.

В обратной ситуации, при негативных прогнозах, их доля сокращается, и увеличивается доля безрисковых активов, которые позволят гарантировать 100% капитала в конце срока.

Схематично этот процесс показан на рисунке ниже.

Рис. 1

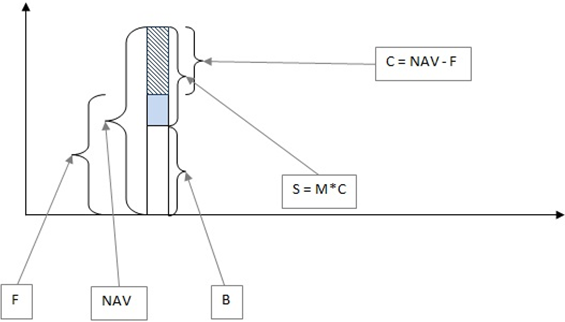
Конфигурация портфеля в начальный момент времени состоит из:

Shares (S) – акции в портфеле;
Bonds (B) – облигации в портфеле;
Net asset value (NAV) – стоимость чистых активов или рыночная стоимость портфеля, определяется как сумма S и B;
Floor (F) – минимальная стоимость портфеля, которая обеспечит 100% возврат капитала;
Cushion (C) – «подушка», определяется как разность между NAV и F;
Multiplier (M) – мультипликатор.

Начальные инвестиции в рискованный актив будут сделаны в соответствии с формулой:

(1)

Значение мультипликатора, как правило, выбирается исходя из предпочтений инвестора относительно риска. Если он готов к снижению рискованной части своего портфеля на x%, то мультипликатор для него будет равен 1/x.

Рис. 2

Перейдем к описанию математической модели. Все стохастические процессы определены на стохастическом базисе . Стохастический базис – это полное вероятностное пространство , с выделенным на нем неубывающим семейством под- σ-алгебр , удовлетворяющих условиям непрерывности справа и пополненности.

Рассмотрим эволюцию стоимости двух финансовых инструментов - акции и облигации.

Безрисковый актив B описывается уравнением:

(2)

где r – постоянная процентная ставка, а B₀=b.

Изменение цены акции или индекса задается геометрическим броуновским движением:

(3)

где – константы, для которых мы предполагаем: и .

Стратегия может быть представлена предсказуемым случайным процессом , который определяет долю стоимости портфеля в момент времени t, инвестируемую в рискованный актив S. В дальнейшем будем рассматривать самофинансируемый портфель, то есть такой, для которого не предполагается добавление или изъятие наличных средств, покупка новых активов осуществляется за счет продажи старых.

V_t обозначает процесс оценки портфеля, который связан со стратегией α, и является решением уравнения:

(4)

Где V₀=x.

используется для обозначения приведенной стоимости G:

(5)

или, что то же самое:

(6)

Таким образом, процесс для «подушки»:

(7)

Если обозначает мультипликатор, то для стратегии CPPI задается соотношением:

(8)

Утверждение 1. Величина портфеля V_t в любой момент времени ∀t∈[0,T] с параметром M задается:

Доказательство утверждения приводится в книгах многих авторов, при желании читатель может найти его, например, в работе “Portfolio Insurance Strategies: OBPI versus CPPI” авторов Philippe Bertrand и Jean-luc Prigent.

Таким образом, можно видеть, что стратегия CPPI параметризована значением F₀ и мультипликатором M.

Можем также получить уравнения, описывающие математическое ожидание и дисперсию процесса V_t.

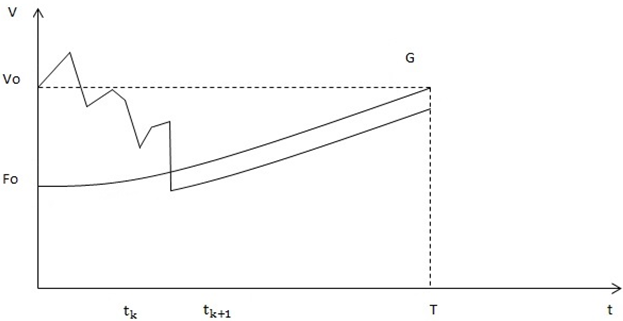
Основной проблемой применения данной стратегии на практике, которая и послужила причиной написания статьи, является так называемый «gap risk», или риск снижения стоимости портфеля ниже минимального уровня . В реальных рыночных условиях, из-за существования, например, транзакционных издержек, изменение структуры портфеля происходит дискретно. Ввиду этого вполне возможна ситуация, при которой стоимость портфеля падает ниже минимального уровня в период между двумя ребалансировками (t_k;t_k₊₁), которые на практике могут происходить еженедельно или ежемесячно. Таким образом, портфельный управляющий сталкивается с риском недостижения необходимого гарантированного уровня стоимости портфеля к назначенной дате. Эта ситуация наглядно продемонстрирована на рисунке.

Рис. 3

Многие авторы выдвигали различные варианты решения этой проблемы. Некоторые занимались тем, что исследовали возможности хеджирования риска с помощью опционов. Однако, в отличие от развитых рынков, в России не так распространены производные финансовые инструменты, что делает весьма затруднительным применение данного подхода. Поэтому более подходящим решением является динамическое изменение значения мультипликатора для стратегии CPPI. Данный метод управления риском способен предложить управляющему верхний предел задания мультипликатора в данный момент времени.

В дискретной стратегии CPPI распределение активов происходит в моменты между равными временными промежутками

Как уже было отмечено ранее максимальная приемлемая просадка определяется значением мультипликатора и равна .

Если падение стоимости произошло в период (t_k;t_k₊₁), r – процентная ставка между t_k и t_k₊₁, то:

(9)

Таким образом:

Поэтому – максимально возможное падение стоимости рискованной части. Стоимость портфеля будет меньше или равна приведенной стоимости в момент времени t_k₊₁; стоимость безрисковых активов растет с безрисковой процентной ставкой.

Рассмотрим же вероятность потерять больше, чем , как меру риска:

(10)

Где x_k обозначает потери по рискованным активам в период (t_k;t_k₊₁). Чем меньше α, тем более жесткими являются требования со стороны инвестора к управлению рисками. Будем предполагать, что α=0.1%.

В связи с постоянными колебаниями цен активов для удовлетворения условия (10) необходимо динамическое изменение значение мультипликатора.

Начнем с того, что опишем характер движения стоимости рискованных активов. Модель SV (Stochastic volatility) вполне подходит для описания фактической волатильности финансового рынка, так как колебания определяются случайным процессом. Таким образом, в дальнейшем будем использовать модель SV для описания характеристик доходности рисковых активов.

Пусть – стоимости активов в соответствующие моменты времени, определим доходность активов как:

В финансовой литературе слово «волатильность» наиболее часто связывают со значением и ценами, описываемыми уравнением

Где W(t) – стандартный винеровский процесс. В случае если μ и σ являются константами, то x_k имеет нормальное распределение и:

Данное уравнение может быть преобразовано заменой σ на положительную случайную величину σ_k, получим:

(11.1)

z_k – независимые одинаково распределенные случайные величины.

x_k может принимать и отрицательные значения.

Если процесс для представления доходности может быть представим уравнением (11.1), будем называть σ_k стохастической волатильностью. Оценки могут быть получены из:

(11.2)

η_k – независимые нормально распределенные случайные величины с распределением N(0,τ²), μ является константой и обозначает ожидаемые потери по рискованным активам, v и φ также константы, а z_k и η_k взаимно независимые. Из формулы (10) получаем:

(12)

Где f(x_k) функция плотности распределения. Немного преобразуем:

(13)

Отсюда находим M_k:

(14)

Соответственно σ_k может быть получено из оценки модели стохастической волатильности, а функцию предстоит оценить.

В стандартной модели стохастической волатильности z_k – независимые нормально распределенные случайные величины. При практическом же применении модели, из-за того, что доходности активов не описываются нормальным распределением, предполагается использование t-распределения, обобщенного нормального распределения и смешанного нормального распределения для описания эксцесса, асимметрии и толстого хвоста доходностей активов.

Будем использовать теорию экстремальных значений (extreme value theory) для описания z_k из формулы (14), так как основной интерес представляют именно экстремальные значения потерь, то есть та часть распределения, где они рекордно большие. Использование этого подхода позволит описать только хвост распределения, что в свою очередь позволит избежать предположений обо всем распределении, что увеличивает точность модели. Кроме того, экстремальное значение редко встречается в реальных данных, и эффективность оценки будет зависеть от оценки квантили распределения. Тем не менее, EVT делает экстраполяцию, основываясь на гладкости распределения, таким образом, показывая всю форму хвоста, а не значения нескольких потерь, поэтому он идеально подходит для оценки с таким широким доверительным интервалом.

Теория экстремальных значений используется именно в случаях необычных явлений и событий с небольшими вероятностями. Существует два подхода для практического применения метода [1,4,7]. Первый подход основан на выделении серии блоков максимумов (минимумов). Во многих ситуациях принято извлекать годовые максимумы (минимумы), генерируя «Annual Maxima Series». Второй подход основан на выделении пиковых значений ряда, превышающих определенный порог (падает ниже определенного порогового значения) в течение периода. Этот способ обычно называют как "Peak Over Threshold". Таким образом, в заданный год он может привести к формированию целого ряда значений, а может и не выделить ни одного значения вовсе. В нашем случае целесообразно использовать именно второй подход, он позволит более эффективно использовать исходные данные, в случае превышения наблюдаемой переменной определенного достаточно большого порогового значения.

F(x) обозначает неизвестную функцию распределения переменной X, и мы хотим оценить условную функцию распределения F_u переменной X, которая выше определенного порогового значения u, достаточно большого для применения EVT; количество значений, превышающих порог, обозначим за , – те самые значения, пусть также , где x₊ правый конец исходного распределения, тогда распределение потерь, превышающих пороговое значение:

(15)

Данная функция описывает распределение значений, превышающих пороговое при условии, что порог превышен.

Теорема 1 (Pickands–Balkema–de Haan). Пусть x₁,x₂,… независимые и одинаково распределенные случайные величины, а F_u – их распределение «превышений». Тогда если u →x₊, то

Где G_ξ_,_β – обобщенное распределение Парето:

Ξ – параметр формы, β – параметр масштаба.

Тогда из (15) получим:

(16)

Если N обозначает общее количество наблюдаемых значений, то очевидно, что . Получим:

(17)

Наконец, получаем выражение для :

(18)

Подставляя в формулу (14) для мультипликатора:

(19)

Полученная формула отражает зависимость значения мультипликатора от рискованных активов, частоты появления экстремальных значений и ожидаемых потерь [3,6]. Анализируя полученную формулу, становится ясно, что при сильных рыночных колебаниях цен необходимо сократить значение мультипликатора, чтобы избежать риска. Если ξ становится все больше, то мультипликатор наоборот должен становиться меньше. Параметр ξ зависит от формы распределения и показывает тяжесть хвоста. Таким образом, если экстремальные значения потерь появляются чаще, степень риска должна быть уменьшена. Параметр μ обозначает ожидаемые потери, поэтому при маленьких значениях данного параметра есть смысл принять риск и увеличить мультипликатор. Интуитивно понятно, что доля рискованных активов в портфеле должна быть увеличена при преобладании бычьего тренда на рынке, однако формула (19) показывает, что с точки зрения управления рисками инвестор или управляющий при выборе мультипликатора должен учитывать и иные факторы.

Для расчетов были выбраны недельные доходности индекса РТС [5,7] за последние десять лет. Этот временной промежуток учитывает мировой финансовый кризис 2008 года и кризис, начавшийся в России в 2014, таким образом можно будет проанализировать, какое влияние оказывает повышенная неопределенность на значении мультипликатора. Ниже представлены некоторые результаты расчетов.

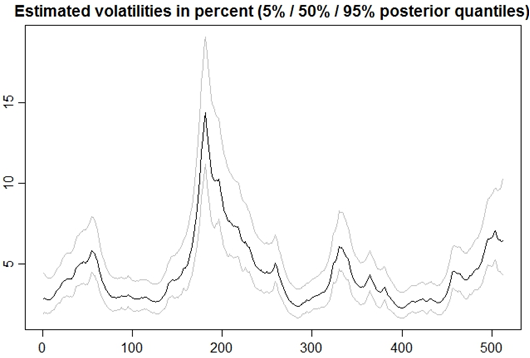
Полученные результаты для волатильности:

Рис. 4

Рис. 5

Рис. 6

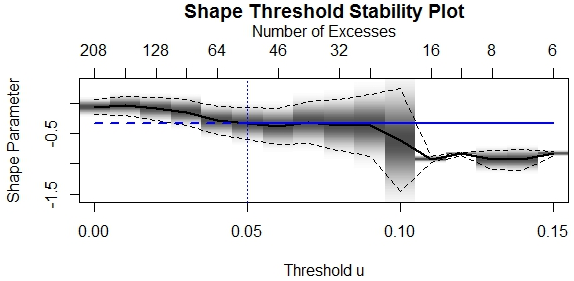
Процесс выбора порогового значения:

Проанализировав результаты графика, выбираем пороговое значение равное u=0.092, при котором параметр распределения ξ относительно стабилен.

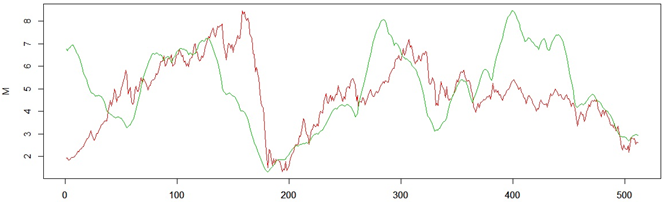
Зеленым цветом на графике ниже показано полученное значение мультипликатора, красным – эволюция индекса РТС за последние десять лет.

Глядя на результаты, можно заметить, что верхняя граница задания мультипликатора находится в диапазоне приблизительно от 2 до 8, что вполне согласуется с применением стратегии CPPI на практике [1,2]. На последнем рисунке также можно видеть, как монотонно уменьшается значение мультипликатора в кризисный период, начиная с середины 2007 года, когда на рынке присутствовала повышенная неопределенность, при этом сам индекс показал существенное снижение немного позже – лишь в конце 2007 года.

Таким образом, в работе были описаны важные для управляющих инструменты, которые позволяют контролировать риски экстремальных потерь, а также выбирать требуемый инвестором уровень этого риска. Полученная модель связывает между собой ожидаемые потери по рискованным активам, вероятность наступления чрезвычайных событий и изменяющуюся во времени волатильность, позволяя, таким образом, исходя из рыночных условий, принимать решение относительно размера рискованной части портфеля. Окончательные результаты расчетов продемонстрировали высокую надежность и сильную прогнозную силу улучшенной стратегии в условиях российского рынка, что говорит о возможности применения на практике построенной модели.

Литература

Philippe Bertrand, Jean-luc Prigent, “Portfolio Insurance Strategies: OBPI versus CPPI”
Sven Balder, Michael Brandl, Antje Mahayni “Effectiveness of CPPI Strategies under Discrete–Time Trading”
Rama Cont, Peter Tankov, “Financial modelling with Jump Processes”
Gregor Kastner, “Dealing with stochastic volatility in time series using the R package stochvol”
Stephen J. Taylor, “Modeling stochastic volatility: A review and comparative study”
Siddhartha Chib, Federico Nardari, Neil Shephard, “Markov chain Monte Carlo methods for stochastic volatility models”
Renate Meyer, Jun Yu, “BUGS for a Bayesian analysis of stochastic volatility models”