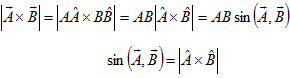О ВОЗМОЖНОСТИ СОЗДАНИЯ СИСТЕМЫ ВЕЛИЧИН МЕХАНИКИ, ЛИШЁННОЙ ОДНОИМЁННЫХ ВЕЛИЧИН (ЧАСТЬ II)

Терещенко В. Г.

Доцент, кандидат технических наук, Северо-Кавказский федеральный университет

О ВОЗМОЖНОСТИ СОЗДАНИЯ СИСТЕМЫ ВЕЛИЧИН МЕХАНИКИ, ЛИШЁННОЙ ОДНОИМЁННЫХ ВЕЛИЧИН (ЧАСТЬ II)

Аннотация

Проведены исследования в области теоретической метрологии, механики и геометрии. Цель – усовершенствование системы величин механики, достижение взаимного однозначного соответствия между размерностью и родом величины. Предложена универсальная форма записи величин механики и соответствующая форма записи их размерностей. Найдёт применение в метрологии, образовании, компьютерных вычислениях.

Ключевые слова: метрология, система величин, размерность, механика, геометрия.

Tereshchenko V. G.

Associate professor, PhD in Engineering, North-Caucasus Federal University

ABOUT POSSIBILITY OF CREATION OF SYSTEM OF QUANTITIES OF THE MECHANICS DEPRIVED OF THE QUANTITIES OF THE SAME NAME (PART II)

Abstract

Researches in the field of theoretical metrology, mechanics and geometry are conducted. Goal – improvement of the system of mechanics quantities, the achievement of mutual-one correspondence between a dimension and a kind of quantity. The universal form of record of quantities of mechanics and the corresponding form of record of their dimensions is offered. Will applications in metrology, education, computer calculations.

Keywords: metrology, system of quantities, dimension, mechanics, geometry.

Данная статья является продолжением нашей публикации в этом журнале [1], посвящённой такому усовершенствованию системы величин механики, при котором исчезнут (полностью или частично) одноимённые величины. Двигаясь к поставленной цели, мы пришли к необходимости добавить в систему величин направление D в качестве четвёртой основной величины механики. Объединение направления с величиной длины отличается от умножения и деления. Предложено [1, 2] объединение размерности направления D с размерностью длины в нулевой степени L⁰ обозначать знаком ◦. Тогда размерность единичного вектора D◦L⁰ не равна размерности направления. Объединение D◦L⁰L=D◦L означает измерение длины в данном направлении (параллельно данной прямой оси). Размерность, как выражение в форме степенного одночлена, строится на основании уравнения связи между величинами. Следовательно, отличия между величинами могут быть потеряны в уравнении связи или при переходе от него к формуле размерности. Возникла задача исследования и уточнения уравнений связи между величинами и адекватного переноса в формулу размерности величин и математических действий. До сих пор в качестве уравнений связи не использовались формулы высшей математики, в частности, действия с векторами. В [1, 2] предложено использовать действие скалярного умножения векторов в формулах размерности, т.е. взять скалярное произведение в качестве уравнения связи. Логично также рассмотреть возможность использования векторного произведения.

Если определяющая физическая формула содержит векторное произведение, то уравнение связи и размерность такой величины тоже должны содержать векторное произведение. В общем случае величина, полученная путём векторного произведения, должна иметь размерность вида

   (1)

которую можно записать [2] и так D◦1×D◦1L^αM^βT^γ. Здесь M, T – размерности массы и времени; α, β, γ – показатели степени, называемые показателями размерности. Величины такого типа называют псевдовекторами за то, что выбор одного из двух возможных для них направлений на перпендикуляре к обоим сомножителям зависит от выбора правой или левой системы координат. Но изменить направление вектора на противоположное направление можно изменением знака модуля, умножением на отрицательную скалярную величину, не изменяя размерности. Поэтому для размерностей важны более фундаментальные свойства векторного произведения. Размерность должна отображать род (физический смысл) величины. Векторное произведение направлений имеет смысл направления, перпендикулярного к направлениям обоих сомножителей. Т.о. векторное произведение задаёт ориентиры направлений в трёхмерном пространстве на базе двух заданных векторов. Это превращение плоской задачи в пространственную. Также нужно отметить полное отсутствие измерения длины в направлении результата векторного произведения. Направление указано, но не объединено с собственным расстоянием. Вектор-результат не может быть представлен линейной комбинацией двух векторов сомножителей.

Пример – размерность момента силы относительно точки D◦L⁰L×D◦L⁰LM¹T^-2. Она отличается от размерности работы [1] векторным характером умножения направлений. Другой пример – размерность векторного произведения двух единичных векторов D◦L⁰×D◦L⁰.

Используем известное [3] представление вектора , как произведения его абсолютной величины A на единичный вектор (орт) . В соответствии с определением векторного произведения для векторов  и 

      (2)

и с учётом предложенной в [1] размерности орта  следует размерность синуса угла между направлениями или векторами

     (3)

Таким образом, модуль (абсолютная величина, а лучше сказать – скалярная часть) размерности векторного произведения двух единичных векторов есть размерность синуса угла. Модуль величины получим, если отвлечься от направления, т.е. разъединить направление с модулем и отбросить направление. Эти действия предлагаем формально записать так

     (4)

Здесь получили размерность величины, числовое значение которой находится в пределах от -1 до 1. Такую величину можно назвать нормированным модулем. Сомножители с размерностью L⁰ (безразмерные единицы) тоже будем называть нормированными модулями. Между собой они не перемножаются как скаляры. Их векторное произведение возвращает значение синуса угла между направлениями, с которыми они объединены.

Приходим к выводу, что векторную величину  можно представить, как «собранную» из трёх элементов

     (5)

где      (6)

 – направление вектора  и нормированного вектора ;  – нормированный модуль; A – размерностный модуль с размерностью L^αM^βT^γ;  – нормированный вектор, в частности, единичный. (Обозначения  и  записаны при помощи индекса сверху). Такое представление векторной величины соответствует предложенной в [1] размерности вектора, которую в общем виде можно записать как

     (7)

Словесное определение вектора можно уточнить, добавив, что модуль вектора есть произведение нормированного и размерностного модулей.

При записи формулы (4) мы предположили, что действие векторного произведения может быть отдельно произведено с направлениями и отдельно произведено с нормированными модулями. Затем результаты этих действий объединяются как направление и нормированный модуль полученной величины. Аналогично можно поступать и при записи скалярного умножения векторов.

Каждый элемент вектора играет свою роль при умножении векторов. Направления, перемножаясь между собой, в векторном произведении создают новое нормальное к обоим направление, а в скалярном произведении образуют скаляр. Нормированные модули участвуют в векторном и скалярном произведении и возвращают значение синуса угла между векторами при векторном произведении и значение косинуса – при скалярном произведении. Размерностные модули перемножаются как скалярные величины.

Размерности величин, полученных скалярным или векторным умножением векторов, тоже, в общем случае, состоят из трёх элементов. В каждом элементе содержится запись соответствующего умножения. Но результат скалярного умножения векторов – это скаляр. Следовательно, предлагаемая форма записи размерности в системе DLMT может стать универсальной.

Вернёмся к скалярному произведению (формулы 5 и 6 из [1]). Скалярное произведение векторов возвращает скаляр второго рода [4] (с. 30) или третьего [5]. Поэтому в формуле (6) из [1] скалярное произведение направлений D•D равносильно отсутствию знака направления.

     (8)

     (9)

Это размерность нормированного модуля. Скалярное произведение

     (10)

имеет размерность

     (11)

где показатели степени α=α_A+α_B, β=β_A+β_B, γ=γ_A+γ_B получены сложением показателей степени при одинаковых основных величинах в размерностях сомножителей A и B.

Скалярное произведение нормированных модулей, т.е. косинус угла между направлениями сомножителей, зависит от этих направлений. В частности, при замене одного направления на противоположное ему направление, результат меняет знак. Это и является признаком скаляров второго (или третьего) рода.

Сравним с векторным произведением нормированных модулей, т.е. с синусом угла между направлениями сомножителей (формулы 2 и 4). Поскольку знак синуса зависит от направления отсчёта угла (по часовой стрелке или против), то знак величины, содержащей синус, зависит от последовательности сомножителей и принятой правой или левой тройки векторов. Как следствие, выбор направления на перпендикуляре к сомножителям зависит от принятой тройки векторов. Это является признаком псевдовектора. Как известно, скалярное произведение истинного вектора и псевдовектора является псевдоскаляром. Это результат умножения синуса на косинус в рамках действий с нормированными модулями.

Проекция вектора на направление единичного вектора и её размерность

     (12)

     (13)

где L^αM^βT^γ – размерность размерностного модуля A вектора .

Как известно, «если проекцию на ось помножить на орт этой оси, то получим векторную величину, называемую составляющей по оси» [4].

     (14)

     (15)

В формуле (14) есть обычное умножение единичного модуля на нормированный модуль, а в формуле (15) умножение их размерностей. Полагаем, что такое умножение эквивалентно умножению на единицу и единичный модуль может быть сокращён в записи, как и его размерность. При этом в записи сохраняется объединение направления с нормированным модулем.

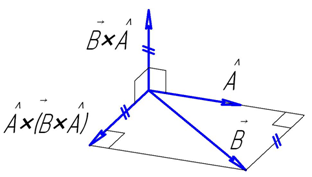
В физических законах и уравнениях связи между величинами отражаются объективные связи, не зависящие от наблюдателя, в частности, не зависящие от произвола в выборе системы координат. Пространство считаем однородным и изотропным. Нет всеобщей системы координат, всеобщего начала отсчёта и всеобщего начального направления. Поэтому направления, как и расстояния, определяются относительно заданных величин. Достаточно назвать некоторое направление первым и относительно него указать второе направление, задав угол между первым и вторым направлением. Направления могут быть указаны в комплексе с другими величинами в форме векторов. Образуется естественная система отсчёта направлений. Выше шла речь об ортогональном проецировании одного из таких заданных объективных направлений (векторов) на другое с помощью скалярного умножения векторов. Рассмотрели мы и получение третьего независимого направления при помощи векторного произведения векторов. Осталось не названным такое действие умножения направлений, которое возвращало бы направление, компланарное направлениям обоих сомножителей (параллельное их плоскости). Хотя при решении геометрических задач фактически такое действие часто используется, когда вектор проецируется на плоскость, перпендикулярную другому заданному направлению. С геометрической точки зрения требуется описать такое действие, которое возвращало бы вектор, перпендикулярный лишь одному из заданных векторов-сомножителей и компланарный обоим. С математической точки зрения это действие должно возвращать вектор, который может быть получен линейной комбинацией двух векторов-сомножителей. Вводить специальное действие умножения векторов, возвращающее ортогональную проекцию вектора на плоскость, излишне, т.к. необходимое действие можно получить путём двойного векторного произведения с участием двух заданных направлений.

Рассмотрим операцию ортогонального проецирования вектора на плоскость. На рисунке 1 показан вектор  – первый из заданных, тот, которого нужно спроецировать на плоскость. Положение плоскости в пространстве задаёт перпендикулярный к ней единичный вектор  – второй заданный вектор. Двойное векторное произведение  есть ортогональная проекция вектора  на плоскость, перпендикулярную к единичному вектору .

Рис. 1 - Ортогональная проекция вектора на плоскость

Величину этой проекции и её размерность можно записать так

     (16)

     (17)

В формуле (16) повторное векторное умножение единичного нормированного модуля сокращено, поскольку направления сомножителей перпендикулярны друг другу, а синус прямого угла равен единице

     (18)

В формуле (17) применена запись , означающая размерность направления при повторном векторном умножении на то же самое направление. Если не учитывать совпадения направлений, получим размерность вектора – результата двойного векторного произведения, компланарного двум заданным векторам, направленного произвольно в их плоскости

     (19)

Выводы по второй части статьи можно сделать следующие. Предложена универсальная форма записи величин в механике, которая содержит три элемента, характеризующие, соответственно, направление, нормированный модуль и размерностный модуль. Нормированный модуль – это коэффициент искажения при ортогональном проецировании. Предложена форма записи размерностей величин в механике, содержащая три аналогичных элемента. Удалось зафиксировать в формулах размерности различия между величинами, получаемыми скалярным, векторным произведением векторов, двойным векторным произведением. Учтены различия, обусловленные повторным использованием одного направления.

Литература

1. Терещенко В.Г. О возможности создания системы величин механики, лишённой одноимённых величин (Часть I) // http://research-journal.org/: Международный научно-исследовательский журнал. — 2015. URL: http://research-journal.org/wp-content/uploads/2011/10/5-2-36.pdf (дата обращения 16.06.2015).
2. Терещенко В.Г. О возможности учёта геометрических свойств физической величины в формуле размерности // Актуальные проблемы строительства, транспорта, машиностроения и техносферной безопасности: материалы III-eй ежегодной научно-практич. конф. Северо-Кавказского федерального университета «Университетская наука – региону». – Ставрополь: ООО ИД «ТЭСЭРА», 2015. – С. 227-233.
3. Киттель Ч., Найт У., Рудерман М. Механика. Берклеевский курс физики: Учебник для вузов. 3-е изд., стер. – СПб.: Издательство «Лань», 2005. – 480 с.
4. Гернет М.М. Курс теоретической механики: Учебник для вузов. – 4-е изд., перераб. и сокр. – М.: Высш. школа, 1981. – 304 с.
5. Терещенко В.Г., Азотова Е.Н. Геометрические свойства физических величин // Актуальные проблемы строительства, транспорта, машиностроения и техносферной безопасности: материалы III-eй ежегодной научно-практич. конф. Северо-Кавказского федерального университета «Университетская наука – региону». – Ставрополь: ООО ИД «ТЭСЭРА», 2015. – С. 221-227.

References

1. Tereshchenko V.G. O vozmozhnosti sozdanija sistemy velichin mehaniki, lishjonnoj odnoimjonnyh velichin (Chast' I) // http://research-journal.org/: Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. — 2015. URL: http://research-journal.org/wp-content/uploads/2011/10/5-2-36.pdf (data obrashhenija 16.06.2015).
2. Tereshchenko V.G. O vozmozhnosti uchjota geometricheskih svojstv fizicheskoj velichiny v formule razmernosti // Aktual'nye problemy stroitel'stva, transporta, mashinostroenija i tehnosfernoj bezopasnosti: materialy III-ej ezhegodnoj nauchno-praktich. konf. Severo-Kavkazskogo federal'nogo universiteta «Universitetskaja nauka – regionu». – Stavropol': OOO ID «TJeSJeRA», 2015. – S. 227-233.
3. Kittel' Ch., Najt U., Ruderman M. Mehanika. Berkleevskij kurs fiziki: Uchebnik dlja vuzov. 3-e izd., ster. – SPb.: Izdatel'stvo «Lan'», 2005. – 480 s.
4. Gernet M.M. Kurs teoreticheskoj mehaniki: Uchebnik dlja vuzov. – 4-e izd., pererab. i sokr. – M.: Vyssh. shkola, 1981. – 304 s.
5. Tereshchenko V.G. Azotova E.N. Geometricheskie svojstva fizicheskih velichin // Aktual'nye problemy stroitel'stva, transporta, mashinostroenija i tehnosfernoj bezopasnosti: materialy III-ej ezhegodnoj nauchno-praktich. konf. Severo-Kavkazskogo federal'nogo universiteta «Universitetskaja nauka – regionu». – Stavropol': OOO ID «TJeSJeRA», 2015. – S. 221-227.