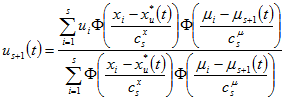О МОДЕЛИРОВАНИИ АКТИВНЫХ СИСТЕМ В УСЛОВИЯХ КОНКУРЕНТНОЙ СРЕДЫ
Попов А. М.1, Стрельников А. В.2
1Доктор физико-математических наук, 2Аспирант, Сибирский государственный аэрокосмический университет имени акадимика М.Ф. Решетнева
О МОДЕЛИРОВАНИИ АКТИВНЫХ СИСТЕМ В УСЛОВИЯХ КОНКУРЕНТНОЙ СРЕДЫ
Аннотация
Целью настоящей статьи является исследование выбора стратегии человека в условиях конкурентной среды. В ходе исследования моделируется поведение человека и создается конкурентоспособный алгоритм. Для создания модели используются методы идентификации, основанные на использовании статистических данных. В статье исследуется задача моделирования активных систем в условиях конкурентной среды. Проверяются гипотеза о том, какого рода – произвольного или случайного – решения принимает человек в этих условиях. Для проверки гипотезы разрабатывается и реализуется эксперимент, который представляет собой конкурентную игру между человеком и компьютером. В игре присутствует система подсчета очков, которая позволяет определить победителя в игре. Приводятся результаты экспериментов, на основании которых можно сделать вывод о проверяемой гипотезе. Результаты содержат статистические обработки накопленной информации. Моделирование стратегии выбора человека позволит составить более сложную модель поведения группы людей. Это в свою очередь поможет более качественно управлять сложными активными системами. Такими являются любая компания или организация, в том числе и коллективы по исследованию и освоению космического пространства. Также модель поведения группы людей позволит исключить конфликты внутри группы. Эмоциональная стабильность очень важна для экипажей космического корабля.
Ключевые слова: активные системы, стратегия принятия решений, моделирование.
Popov A. M.1, Strelnikov A.V.2
1PhD in Physics and Mathematics, 2Postgraduate student, Siberian State Aerospace University
ON ACTIVE SYSTEMS MODELLING IN COMPETITIVE ENVIRONMENT CONDITIONS
Abstract
The purpose of this article is to study the person choice of strategy in a competitive environment. In the studies the model of the person behavior is designed and a competitive algorithm is created. The identification methods based on statistical data are used to create the model. The task of active systems modelling in competitive environment is researched in the article. Hypothesis about the kind of decisions – arbitrary or random – are made by people in these conditions is tested. To verify the hypothesis an experiment is developed and implemented, which is a competitive game between man and computer. The game has a scoring system, which allows determining the winner in the game. The results of experiments on the basis of testable hypothesis can be concluded are shown. The results include statistical processing of the accumulated information. Modeling of the person choosing strategy will allow making a more complex model of the people groups’ behavior. This in turn will help to more efficiently manage the complex active systems. These are any company or organization, including the groups in the exploration and development of space. Also model of the people groups’ behavior will allow eliminating conflicts within the group. Emotional stability is very important for the crew of the spacecraft.
Keywords: active systems, decision making strategy, modelling.
Введение. Статья посвящена исследованию активных систем в условиях конкурентной среды [1]. Активная система содержит элементы, которые имеют волю выбора, – активные элементы. Подобные системы также называются организационными [2]. Как правило, активным элементом является человек. Но в качестве такого элемента может выступать и любой другой своевольный субъект. Например, это может быть какое-либо животное или растение, искусственный разум или группа людей. Хотя иногда группа людей воспринимается как стохастическая система, а не активный элемент, но к этому мы еще позже вернемся.
Моделирование человека считается очень сложным процессом. Это аргументируется тем, что он содержит слишком много переменных [3] и его действия сложно предугадать [4-5]. Поэтому в модели человек отражается как статистическая система, подчиняющаяся каким-либо случайным законам распределения, или как случайная величина. Обычно человек в процессе принятия решений не ориентируются на случайные числа. Более того, человек не способен генерировать случайные числа без специальных инструментов, которые моделируют случайность благодаря несовершенству памяти человека и его ощущению времени и пространства.
Первая гипотеза, которая проверяется в этой статье, заключается в доказательстве того, что человек не генерирует случайные числа для принятия решения в условиях конкурентной среды. Вторая гипотеза заключается в проверке распространения этого правила на группу людей.
Моделирование поведение человека позволит более эффективно управлять группой людей. Это важно для коллективов по изучению и освоению космоса.
Постановка задачи моделирования активной системы. Объектом моделирования является активная система в условиях конкурентной среды. Конкурентная среда означает, что участники системы имеют разные цели и стремятся изменить систему таким образом, чтобы достигалась их собственная цель. Поэтому в этой статье мы будем рассматривать не просто задачу построения модели активной системы, а задачу построения управления этой системой. С технической точки зрения ничего не изменится, мы лишь сразу находим применение искомой модели.
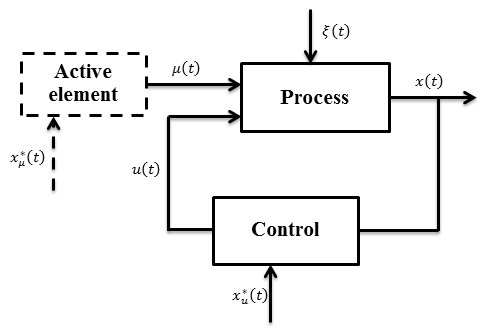
В исследуемой системе присутствуют как минимум двое соперников. Задача рассматривается с точки зрения одного из соперников. Также, помимо двух соперников, принимающих решение произвольно, существует элемент, который преобразует решение двух соперников в результат. Схематично активную систему можно изобразить следующим образом (рис. 1).
Рис. 1 - Схема активной системы в условиях конкурентной среды
На схеме, изображенной на рис. 1, блок Process представляет собой элемент, который преобразует решения двух соперников в результат. Это могут быть правила игры, законы природы или особенности рынка. Блок Active Element описывает действия соперника, а блок Control – наши действия. На схеме ![]() – выходная переменная процесса,
– выходная переменная процесса, ![]() – входная контролируемая переменная процесса,
– входная контролируемая переменная процесса, ![]() – входная неконтролируемая переменная процесса,
– входная неконтролируемая переменная процесса, ![]() – случайное воздействие. Переменные
– случайное воздействие. Переменные ![]() и
и ![]() – желаемые траектории для выходной переменной игроков µ и u соответственно.
– желаемые траектории для выходной переменной игроков µ и u соответственно.
Действия конкурента, как и его стратегия, никогда неизвестны. Поэтому блок Active Element выделен пунктиром. Цель конкурента ![]() обычно можно вывести из правил игры, т.е. она известна, однако эта информация редко используется в известных моделях [6]. К тому же конкурент волен изменять свои предпочтения только для того, чтобы запутать других игроков. В зависимости от задачи блок Process может быть известен, неизвестен или известен с точностью до параметров.
обычно можно вывести из правил игры, т.е. она известна, однако эта информация редко используется в известных моделях [6]. К тому же конкурент волен изменять свои предпочтения только для того, чтобы запутать других игроков. В зависимости от задачи блок Process может быть известен, неизвестен или известен с точностью до параметров.
Задачей игрока ![]() является разработка стратегии (построение управления), которая приведет его к цели
является разработка стратегии (построение управления), которая приведет его к цели ![]() .
.
Существует несколько подходов к моделированию управления. Сославшись на сложность стратегии человека, мы можем рассматривать ![]() как случайную величину, подчиняющуюся равномерному закону распределения. В этом случае, блок Active element будет отсутствовать в схеме. Вторым подходом является построение статистических предпочтений игрока
как случайную величину, подчиняющуюся равномерному закону распределения. В этом случае, блок Active element будет отсутствовать в схеме. Вторым подходом является построение статистических предпочтений игрока ![]() . Здесь мы не учитываем его цель
. Здесь мы не учитываем его цель ![]() . Еще один подход заключается в том, что в модели стратегия конкурента рассматривается как полноценная система управления. В зависимости от накопленной информации вычисляется оптимальное решение
. Еще один подход заключается в том, что в модели стратегия конкурента рассматривается как полноценная система управления. В зависимости от накопленной информации вычисляется оптимальное решение ![]() с точки зрения выбранного критерия. После этого вычисляется
с точки зрения выбранного критерия. После этого вычисляется ![]() с учетом спрогнозированного значения
с учетом спрогнозированного значения ![]() .
.
Задачей настоящего исследования является проверка описанных ранее гипотез с использованием описанных подходов к моделированию управления. Исследуются различные подходы, потому что разные стратегии оказывают разное влияние на стратегию принятия решения конкурента.
Описание эксперимента. Для решения поставленной задачи реализуем эксперимент. Он представляет собой игру для двоих игроков-соперников: компьютера u и человека µ.
Правила игры довольно просты. Задача каждого из игроков набрать сумму очков больше, чем у соперника. Начальные суммы очков равны нулю для каждого игрока. Игра длится заданное количество ходов.
В течение каждого хода оба игрока вводят числа ![]() , в пределах [-1;1], исключая 0. Два числа перемножаются
, в пределах [-1;1], исключая 0. Два числа перемножаются ![]() . Если результат
. Если результат ![]() , то игрок
, то игрок ![]() получает
получает ![]() очков. Если результат
очков. Если результат ![]() , то игрок
, то игрок ![]() получает
получает ![]() очков. Можно ввести в игру порядок округления для упрощения восприятия.
очков. Можно ввести в игру порядок округления для упрощения восприятия.
Эксперимент заключается в том, что на одном и том же человеке тестируются все три подхода. В зависимости от выбранного подхода человек по-разному адаптируется к конкурентной среде. Это подтвердят статистические гипотезы, если ходов достаточное количество. Помимо этого в случае, если стратегия одного из игроков является случайной, т.е. его решение является значением случайной величины с равномерным законом распределения с параметрами [-1;1], исключая 0, то результат игры будет близкий к ничье. Первый подход представляет собой случайную стратегию, два других – нет.
Для соблюдения чистоты эксперимента человек видит лишь информацию о прошлом ходе. Любая другая статистическая и полезная информация ему недоступна. Человек даже не может догадаться, какой подход сейчас используется, т.к. их порядок перемешивается. Однако никто не ограничивает человека использовать крайние стратегии. Например, вводить одно и то же число. Или использовать доступные генераторы случайных чисел: положение стрелки на часах, ловля линейки, бросание монет. Гипотеза говорит о том, что даже в таком случае выбор человека не будет случайным, т.к. рано или поздно человеку захочется изменить выпавшее случайно решение.
В свою очередь алгоритм не использует введенное человеком число для расчета собственного выбора.
Построение модели системы управления. Любая качественная модель объекта основывается на статистических данных. Эта та особенность моделей, которая приближает их к реальному миру. И наш случай не исключение. Поэтому для построения качественного управления потребуется выборка статистических измерений ![]() , где s – объем выборки.
, где s – объем выборки.
Теоретически, чем больше объем выборки, тем качественнее, в отношении абсолютной ошибки управления, будет модель. Но на практике нашим конкурентом является человек, с феноменальной способностью адаптации к сложным условиям [7-10]. В те моменты, когда конкурент начинает подозревать о своем проигрыше, он меняет свою стратегию. Поэтому для моделирования алгоритма, направленного на победу, рекомендуется сделать его чувствительным к нестационарным системам или встроить индикатор, который мог распознать смену стратегии конкурента. Но целью этого исследования является изучение поведения человека, а не построение конкурентоспособного алгоритма. Следовательно, мы не будем далее акцентировать внимание на способности разработанных алгоритмов противостоять стратегии конкурента.
Модель управления активной системой состоит из двух частей. В первую очередь необходимо спрогнозировать следующий шаг конкурента ![]() . Ранее мы описывали три подхода к решению этой задачи. Первый подход соответствовал ситуации, когда вся информация о конкуренте отсутствует, тогда все возможные его действия имеют равный приоритет. В этом случае значение следующего шага
. Ранее мы описывали три подхода к решению этой задачи. Первый подход соответствовал ситуации, когда вся информация о конкуренте отсутствует, тогда все возможные его действия имеют равный приоритет. В этом случае значение следующего шага ![]() можно считать любым. Например, можно использовать предыдущее значение
можно считать любым. Например, можно использовать предыдущее значение ![]() в надежде на то, что конкурент не будет изменять своего решения. Или можно использовать суперпозицию значений
в надежде на то, что конкурент не будет изменять своего решения. Или можно использовать суперпозицию значений ![]() , т.е. воспринимать в модели
, т.е. воспринимать в модели ![]() как случайную величину.
как случайную величину.
Другой подход заключается в использовании статистической информации – выборке статистических измерений. Для прогнозирования ![]() обычно используют методы прогнозирования рядов [11-12]. В этом случае, следующий шаг находится с помощью построения тенденции ряда
обычно используют методы прогнозирования рядов [11-12]. В этом случае, следующий шаг находится с помощью построения тенденции ряда ![]() . Либо можно использовать модель зависимости:
. Либо можно использовать модель зависимости:
где F – некоторый оператор, p – глубина зависимости.
В третьем подходе к прогнозированию мы рассматриваем систему с точки зрения конкурента и ищем наиболее выгодное для него решение. Задача сильно упрощается, если известна цель конкурента ![]() . Обычно ее можно вывести из самой задачи. Например, когда известны правила игры. Когда этой информации нет, значение цели можно предположить (много денег, победа в игре и прочее). В крайнем случае, можно использовать хитрый прием. Зафиксировать свое решение
. Обычно ее можно вывести из самой задачи. Например, когда известны правила игры. Когда этой информации нет, значение цели можно предположить (много денег, победа в игре и прочее). В крайнем случае, можно использовать хитрый прием. Зафиксировать свое решение ![]() в течение нескольких следующих ходов. Если конкурент не использует случайную стратегию для запутывания оппонента, то значение выхода системы
в течение нескольких следующих ходов. Если конкурент не использует случайную стратегию для запутывания оппонента, то значение выхода системы ![]() будет стремиться к желаемой цели
будет стремиться к желаемой цели ![]() . Для выявления желаемой траектории (не значения) потребуется большее количество шагов.
. Для выявления желаемой траектории (не значения) потребуется большее количество шагов.
В случае если ![]() известна, то модель (1) примет вид:
известна, то модель (1) примет вид:
где ![]() – временные векторы,
– временные векторы, ![]() – непараметрический оператор. Модель (2) является непараметрической, т.к. структура стратегии принятия решений конкурента неизвестна.
– непараметрический оператор. Модель (2) является непараметрической, т.к. структура стратегии принятия решений конкурента неизвестна.
Зная следующий шаг конкурента, можно приступать ко второй части моделирования: вычислению управляющего воздействия ![]() . Пусть блок Process описывается уравнением:
. Пусть блок Process описывается уравнением:
где A – неизвестный оператор.
Управление можно рассчитать путем:
Следовательно, для того чтобы вычислить управление, необходимо оценить обратный оператор ![]() . В зависимости от уровня априорной информации оценка может быть различной. Если, например, правила игры таковы, что
. В зависимости от уровня априорной информации оценка может быть различной. Если, например, правила игры таковы, что ![]() существует и его можно вывести аналитически, тогда управление можно рассчитать с точность до величины
существует и его можно вывести аналитически, тогда управление можно рассчитать с точность до величины ![]() возмущающего воздействия.
возмущающего воздействия.
В ином случае, априорной информации достаточно только для того, чтобы определить оператор A с точностью до параметров. В этом случае мы имеем задачу параметрической идентификации, и модель имеет вид:
где B – параметрический оператор, α – набор параметров.
Если априорной информации недостаточно для определения структуры зависимости, то имеет место задача непараметрической идентификации:
где ![]() – непараметрический оператор. Примером модели (6) может служить непараметрическая оценка Надарая-Ватсона [13]:
– непараметрический оператор. Примером модели (6) может служить непараметрическая оценка Надарая-Ватсона [13]:
где ![]() – ядерная функция,
– ядерная функция, ![]() и
и ![]() – параметры размытости.
– параметры размытости.
Описанные методы не ограничивают исследование. Существует множество других подходов к решению поставленных задач. Также можно комбинировать различные методы и модели. Здесь описаны лишь те алгоритмы, которые были использованы в исследовании.
Результаты экспериментирования. Для проведения экспериментов была создана программа, реализующая процесс игры, описанный ранее, и алгоритмы оценки стратегии конкурента. Первый алгоритм (Random) имел случайную стратегию. Второй (Statistic) оценивал следующий шаг ![]() конкурента, как наиболее вероятный, согласно построенной по статистическим данным оценки плотности вероятности [14-15]. Абсолютным значением управления служила оценка вероятности, с которой конкурент сделает следующий шаг
конкурента, как наиболее вероятный, согласно построенной по статистическим данным оценки плотности вероятности [14-15]. Абсолютным значением управления служила оценка вероятности, с которой конкурент сделает следующий шаг ![]() . Знак управления, естественно, был обратный знаку у
. Знак управления, естественно, был обратный знаку у ![]() . Третий алгоритм (Control) основывался на расчете управления по формуле (7) с учетом, что стратегия конкурента воспринимается, как полноценная система управления.
. Третий алгоритм (Control) основывался на расчете управления по формуле (7) с учетом, что стратегия конкурента воспринимается, как полноценная система управления.
В экспериментах приняло участие 20 человек. Каждый испытуемый соревновался со всеми тремя алгоритмами поочередно. Порядок алгоритмов определялся случайным образом. Результаты игры одного из испытуемых приведены далее.
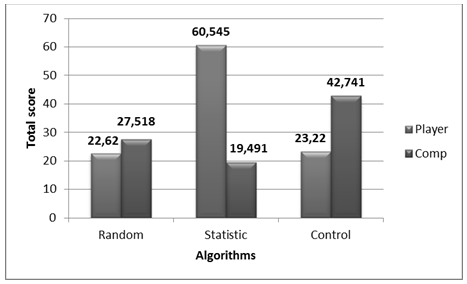
Рис. 2 - Результаты игры одного из испытуемых
На графике, изображенном на рис. 2, по оси ординат располагаются суммарное количество очков, набранные испытуемым и алгоритмом, за 100 туров игры. Левые столбцы соответствуют очкам игрока-человека, а правые – игрока-компьютера.
В целом, результаты игр получились следующие:
- алгоритм Random победил 55% участников;
- алгоритм Statistic проиграл всем участникам;
- алгоритм Control победил 85% участников.
Согласно законам теории вероятности [16-17], если хотя бы один из игроков использует случайную стратегию, то исход игры в большинстве случаях должен быть близок к ничье. В среднем при игре с алгоритмом Random разница между очками игроков была менее 10% от общей суммы. Если никто из игроков, не использует случайную стратегию, то в большинстве случаях выявляется победитель – тот игрок, стратегия которого доминирует. В случаях при игре с алгоритмом Statistic разница между очками игроков в среднем составила более 40% от общей суммы, а с алгоритмом Control – более 25% от общей суммы. В пределах допустимого уровня значимости, результаты говорят о том, что игроки выбирают неслучайную стратегию.
С помощью такого подхода можно только определить случайную или не случайную стратегию использует один человек. Для проверки, выполняется ли эта гипотеза для группы людей, количества участников недостаточно. Однако существует еще один способ узнать, использует ли игрок случайную стратегию или нет.
Участники экспериментов, если судить по их собственным словам, не использовали стратегию, связанную с абсолютной величиной вводимых значений. Многие считали, что важен лишь знак этой величины, т.к. именно он определяет, кому присуждаются победные очки. Приняв этот момент во внимание, можно исследовать стратегию выбора знака вводимой величины.
На первый взгляд, при заданных условиях игры успешной стратегией выбора знака может быть только случайная стратегия. Однако, это не так, и выбор зависит от стратегии оппонента. Таким образом, стратегия выбора знака не будет являться случайной, если текущий ход зависит от предыдущих. В данном случае под зависимостью мы понимаем, что игрок в одинаковых ситуациях сделает одинаковый выбор. Множество таких выборов для различных ситуаций будет определять стратегию игрока.
Рассмотрим множество ситуаций и выборов игроков. В это множество входят переменные, описывающие выбор знака в текущем ходу и ряде предыдущих ходов. Переменная принимает значение «-», если игрок ввел отрицательное число, и «+», если игрок ввел положительное число. В результате, мы имеем пространство всех выборов при всех ситуациях. Если оба игрока имеют абсолютно случайную стратегию, то при достаточно многократном повторении выборов измерения заполнят все пространство. Если в игре будет присутствовать зависимость между выбором и ситуациями, то измерения заполнят лишь часть пространства.
Описанное выше удобнее представить графически. Для этого переведем пространство выборов и ситуаций в двумерное пространство. Для этого поставим в соответствие каждому «+» единицу, а каждому «-» ноль. Сформируем число в двоичной системе измерения из текущего хода и ряда предыдущих. Иными словами, если игрок в текущем ходу выбрал положительное число, а в двух предыдущих ходах вводил отрицательные числа, то число будет равно «100». Переведя двоичные числа в десятеричные, мы сможем получить две переменные, по одной для каждого игрока.
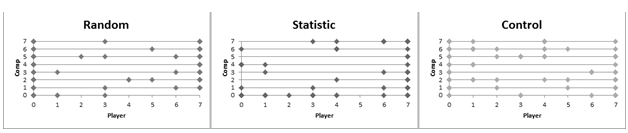
Рис. 3 - Измерения одного игрока в преобразованном пространстве ситуаций и выборов
На рис. 3 изображены измерения одного из участников при играх с тремя алгоритмами. Измерения содержат знаки текущего и двух предыдущих ходов. Измерения заполняют соответственно 44%, 42% и 55% пространства. Значение 25% говорит о том, что оба игрока используют абсолютно неслучайные стратегии. Если измерения заполняют 100%, или близки к 100% с определенным уровнем значимости, то стратегии игроков являются случайными и не зависят от ситуации. Например, при уровне значимости ![]() 100 измерений заполнят подобное пространство только на 80%.
100 измерений заполнят подобное пространство только на 80%.
В среднем по игрокам измерения заполняют 44%, 36% и 54% пространство соответственно для алгоритмов Random, Statistic и Control. Для последнего алгоритма пространство заполнено больше, потому что стратегии меняются чаще, чем при других алгоритмах, в совокупности у обоих игроков. Другими словами, человек-игрок, сталкиваясь с наиболее «сложной» и непредсказуемой стратегией – Random, перестает изменять свою собственную стратегию.
Для того чтобы оценить, насколько присуща случайная стратегия группе людей, соединим измерения всех игроков и представим их в преобразованном пространстве ситуаций и выборов.
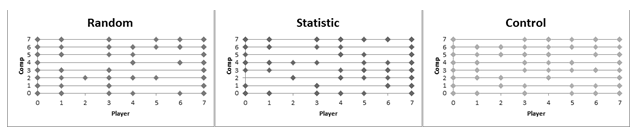
Рис. 4 - Измерения всех игроков в преобразованном пространстве ситуаций и выборов
На рис. 4 представлено 100 случайно выбранных измерений всех игроков в пространстве ситуаций и выборов. Представлена не вся выборка для того, чтобы можно было сравнить, насколько случайна стратегия группы людей и одного игрока. Измерения заполнили пространство на 67%, 68% и 79% для соответствующих алгоритмов. Это означает, что группа людей может формировать случайную стратегию, если организовать случайный выбор человека, стратегия которого будет использоваться. Это вполне очевидный вывод. Но из результатов следует, что группа людей не подчиняется каким-либо определенным законам в смоделированной конкурентной среде. Для построения конкурентноспособного алгоритма требуется, чтобы он мог адаптироваться к любому из игроков в процессе самой игры.
Вывод. Приведенные исследования показали, что человек конкурентной среде не использует случайную стратегию. Для генерации случайности человек использует инструменты и погрешности, связанные с оценкой времени и пространства. Возможно создание алгоритма, который статистически будет побеждать человека при равных условиях. Этот алгоритм использует апостериорную информацию о стратегии человека. Группа людей не имеет общую стратегию в конкурентных средах с двумя сторонами. Результаты этого и дальнейших исследований позволят повысить качество управления организационными системами, которые функционируют в конкурентной среде.
Литература
- Медведев А. В. Теория непараметрических систем. Активные процессы // Вестник Сибирского Государственного Аэрокосмического Университета имени академика М.Ф. Решетнева. – 2012. – №. 2. – С. 55-60.
- Шевчук Д. Управление качеством. – Litres, 2013.
- Новиков Д. А. Методология управления //М.: Либроком. – 2011.
- Ильин А. А., Ильин Р. А., Анкудинов К. А. Математическое обеспечение синтеза математических моделей сложных динамических процессов по выборке данных их предыстории //Известия Тульского государственного университета. Технические науки. – 2012. – №. 3. – С. 305-311.
- Ядов В. А. и др. Саморегуляция и прогнозирование социального поведения личности: Диспозиционная концепция //Квант. – 2014. – №. 1. – С. 2-6.
- Aris R. Mathematical modelling techniques. – Courier Dover Publications, 2012.
- Растригин Л. А. Адаптация сложных систем. Методы и приложения.–Рига: Зинатне, 1981.–394 с.
- Курейчик В. М. Особенности построения систем поддержки принятия решений //Известия ЮФУ. Технические науки. – 2012. – №. 7. – С. 132.
- Исаев Е., Слободчиков В. Психология развития человека. Развитие субъективной реальности в онтогенезе. – Litres, 2014.
- Либина А. Совладающий интеллект: человек в сложной жизненной ситуации. – Litres, 2013.
- Лапыгин Ю., Крылов В., Чернявский А. Экономическое прогнозирование. – Litres, 2013.
- Omelchenko A. V., Rozdimakha E. A., Fedorov A. V. PRediction of self-similar time series containing polynomial trends //Microwave and Telecommunication Technology (CriMiCo), 2013 23rd International Crimean Conference. – IEEE, 2013. – p. 456-457.
- Надарая Э.А. Непараметрические оценки кривой регрессии // Труды ВУ АН ГрССР. Вып. 5. Тбилиси, 1965. С. 55-68.
- Rosenblatt. Remarks on some nonparametric estimates of a density function // Ann. Math. Statist. - 1956. - V.27, № 3. - P. 832-835.
- Parzen. On Estimation of a Probability Density, Function and Mode // IEEE Transactions on Information Theory, vol. Pami-4, №6, 1982.- P. 663-666.
- Осипов В. С. Приложение теории игр к исследованию конкурентного взаимодействия // Наука и бизнес: пути развития. – 2013.
- Пиндайк Р., Рабинфельд Д. Микроэкономика / Пер. с англ. - СПб: Питер, 2011. - 608 с.
References
- Medvedev A. V. [Theory of nonparametric systems. Active processes]. Vestnik SibSAU. 2012, vol. 44, no. 4, p. 55-60. (In Russ.)
- Shevchuk D. Upravlenie kachestvom. [Quality control]. Litres, 2013.
- Novikov D. A. Metodologiya upravleniya. [Methodology of control]. M.: Librocom, 2011.
- Il'in A. A., Il'in R. A., Ankudinov K. A. [Software synthesis of mathematical models of complex dynamic processes the sample data background]. News of the Tula state University. Technical science. 2012, no. 3, p. 305-311. (In Russ)
- Yadov V. A. and others. [Self-regulation and predicting social behavior: Dispositional concept] Quant. 2014, no. 1, p. 2-6. (In Russ)
- Aris R. Mathematical modelling techniques. Courier Dover Publications, 2012.
- Rastrigin L. A. Adaptatsiya slozhnykh sistem. Metody i prilozheniya. [Complex system adaptayion. Methods and applications]. Riga: Zinatne, 1981. 394 p.
- Kureychik V. M. [The characteristics of Decision Support System design]. News UFU. Technical Science. 2012, no. 7, p. 132. (In Russ)
- Isaev E., Slobodchikov V. Psikhologiya razvitiya cheloveka. Razvitie sub"ektivnoy real'nosti v ontogeneze. [Psychology of human development. The development of subjective reality in ontogenesis]. Litres, 2014.
- Libina A. Sovladayushchiy intellekt: chelovek v slozhnoy zhiznennoy situatsii. [Coulduse intelligence: people in difficult life situations]. Litres, 2013.
- Lapygin Yu., Krylov V., Chernyavskiy A. Ekonomicheskoe prognozirovanie. [Economic forecasting]. Litres, 2013.
- Omelchenko A. V., Rozdimakha E. A., Fedorov A. V. [PRediction of self-similar time series containing polynomial trends]. Microwave and Telecommunication Technology (CriMiCo), 2013 23rd International Crimean Conference. IEEE, 2013, p. 456-457.
- Nadaraya E. A. [Nonparametric estimations of regression]. Works VU AN GSSR. Tbilisi, 1965, vol. 5, p. 55-68.
- Rosenblatt. [Remarks on some nonparametric estimates of a density function]. Ann. Math. Statist. 1956, vol. 27, no. 3, p. 832-835.
- Parzen. [On Estimation of a Probability Density, Function and Mode]. IEEE Transactions on Information Theory. 1982, vol. 4, no. 6, p. 663-666.
- Osipov V. S. Prilozhenie teorii igr k issledovaniyu konkurentnogo vzaimodeystviya. [The application of game theory to the study of competitive interactions]. Science and business: development paths, 2013.
- Pindayk R., Rabinfel'd D. [Microeconomic]. Translated by SP: Piter, 2011. 608 p.