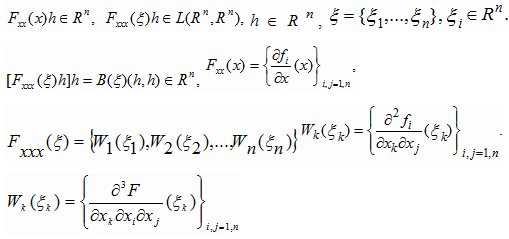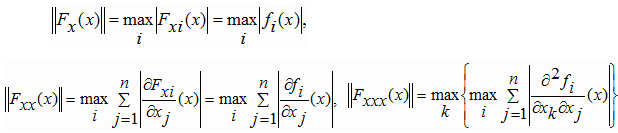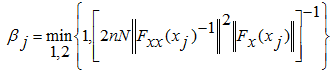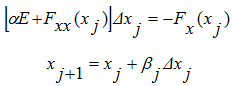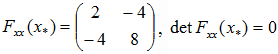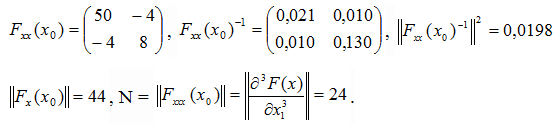МЕТОД НЬЮТОНА ДЛЯ НАХОЖДЕНИЯ ЭКСТРЕМУМОВ СИЛЬНЫХ ВЫПУКЛЫХ ФУНКЦИОНАЛОВ

Бамадио Б.¹, Лебедев К.А.²

¹Аспирант, ²Доктор физико-математических наук, Кубанский государственный университет

МЕТОД НЬЮТОНА ДЛЯ НАХОЖДЕНИЯ ЭКСТРЕМУМОВ СИЛЬНЫХ ВЫПУКЛЫХ ФУНКЦИОНАЛОВ

Аннотация

В статье представлен способ, обобщающий метод решения нелинейных уравнений на отыскание экстремума функций. На текстовых примерах диссертации показано, что метод расширяет область сходимости с разных начальных приближений, заведомо не удовлетворяющих достаточным условиям сходимости классического метода Ньютона.

Ключевые слова: метод ньютона, экстремум, выпуклый функционал

Bamadio B.¹, Lebedev K.A.²

¹Postgraduate student, ²PhD in Physics and Mathematics, Kuban State University

NEWTON'S METHOD FOR FINDING EXTREMUM OF STRONGLY CONVEX FUNCTIONALS

Abstract

In this article the generalized method for solving nonlinear equations for finding the extremum of functions is presented. In the thesis, the examples show that the method of expanding the domain of convergence from different initial approximations, obviously do not meet sufficient conditions for convergence of the classical Newton's method.

Keywords: Newton method, extremum, convexity of a functional.

The relevance of the problem is for computational mathematics modification of Newton's method for calculating the localized extrema of the strongly convex function in order to expand the area of convergence of the iteration.

A function F(x), defined on a convex set X, is called strongly convex if there exists a constant σ>0 such that

For all x, v∈X and for all α, 0≤α≤1. The constant σ is called strong convexity constant of F(x) on the set X [1].

Optimization Methods and systems of nonlinear equations are closely related. For a given sufficiently smooth mappings: f: G⊂Rⁿ→Rⁿ  and F: G⊂Rⁿ→Rⁿ  in the problem

which creates the problem of finding the roots of equations due to the necessary conditions for extrema in normed spaces where f(x)=F_x(x), f(x)=0.

A theorem on the convergence of Newton's method. Using the results of [2] we can be obtain a corollary of the theorem, with imposing burdensome conditions of smoothness.

Consider the problem of finding the extremum (minimum for certainty) to some closed convex region G⊂Rⁿ of finite-dimensional normed linear space

                (1)

where the function is strongly convex F: G⊂Rⁿ→R on a convex closed set of normalized linear space that ensures the uniqueness of a local minimum x_*∈G [1], [3].

Note that the strongly convex function are a subclass of strictly convex functions for which this result is formulated [1], [3].

We assume sufficient smoothness of the function F(x).

Let us denote f(x)=F_x(x) in [2] and obtain the condition under which  under which the theorem on the convergence of computing Newton process for solving systems of nonlinear equations, with the choice of iterative parameter is satisfied. Solution of the minimization of the function is equivalent to finding the root systems of nonlinear equations F_x(x)=0 or f(x)=0

The Newton algorithm for finding the extremum contains the iterative parameter. In order to ensure the convergence, Newton's method provides a method for selecting the iteration parameter steps.

We assume sufficient smoothness of the strongly convex function F(x) in problem (1).

As noted problem (1) has a unique solution (optimum point x*) and under the conditions a) - b) there exist a region U_* containing  at any point of which x=x̅₀∈U_*⊂G. The classical (β=1) Newton's method for problem (1) converges to the root, but the diameter of the region is small.

Sufficient conditions for the convergence of the process, allow us to allocate in general area  S_*⊂U_* c even smaller diameter diamS_*≤diamU_*≤diamG, and convergence iterations of an arbitrary point x₀∈G is not guaranteed.

The mappings F_xx: R_n→R_n, F_xx: R_n→L(Rⁿ,Rⁿ), B: Rⁿ×Rⁿ→Rⁿ  are given by

Where f(x)=F_x(x), F_x, F_xx, F_xxx, f_x, f_xx - first and second derivatives L (Rⁿ,Rⁿ) - normed linear space of matrices B- the bilinear operator [4].Tthe norm is taken as the m-norm [26]:

Using the notion and notations can prove the theorem as a consequence of the theorem [2] on the convergence of modified (2) - (4) of the Newton defined by the following formulas

                       2)

                                                           3)

               4)

Theorem. If the conditions a) - b) are applied to the process 2) - 4) for the problem (1) for any point x₀∈G in a finite number of steps j = 1 , it leads to the initial approximation x_l=x̅₀∈S_*⊂G, from which the process (2), (3) coincides with the classical Newton's method and converges to the root x_*.

Practical application involves stopping time algorithm, which usually combines two features that the process has reached the specified accuracy. The search process is stopped when approximately the necessary conditions for an extremum is fulfilled

Corollary is formulated for strongly convex functions, whose determinant detF_xx≠0, in practice, however, this value can be very low, especially when used in the reduction of problems with constraints to unconstrained optimization after applying the method of penalty functions. Or it may not belong to a functional class of strongly convex functions and then the condition detF_xx≠0 can not be guaranteed over the entire region G. Therefore, it is feasible to resort to regularization algorithm using small parameter α>0

Where E - is the identity matrix [5].

Hence the solution of system of linear equations always exists. In addition it is possible to select parameters α and β to optimize the process of searching for the extremum or to ensure relaxation properties of the iterative process

It should be noted that the formulas are difficult to use in practice, since the constant N, M in problems of practical content, are usually not always known. However such theorems allow us to specify on the availability principle to resolve one of the most significant shortcomings of the Newton's method, which is to choose a good initial approximation and offer some ways to do this [1], [3].

Test cases for the analysis of the convergence of Newton's method modification. Consider the rate of convergence for the proposed optimization methods on specific test examples

Example. [5]. F(x₁,x₂)=(x₁-2)⁴+(x₁-2x₂)².

This example has been widely used to illustrate the operation of various algorithms in [5].

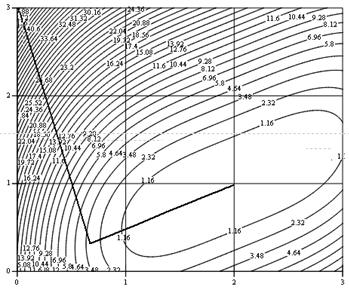
For example, the classical Newton's method converges in 16 steps with an accuracy 

Fig 1. Schedule of convergence of Newton's method

The direct use of formula of corollary is irrational because the limiting value is difficult to assess, and also complication arises from the fact that the function is not strongly convex. The condition b) at the point x_*=(2 1)^T obviously fails.

The idea of the convergent nature of the process can, however, be assessed practically, for example taking a permanent step calculated at the starting point x₀=(0 3)^T.

If we compute the iterative step at the point x0 and take it as a permanent Small step means that the process performs approximately continuous analog of the Newton's method

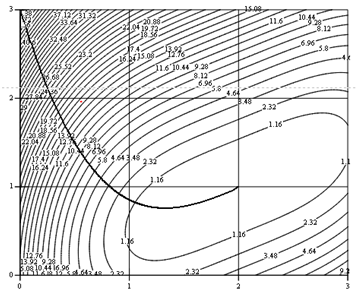
The process converges after 992 steps with precision .

Fig 2. The convergence of Newton's method with a constant step

References

1. Vasilyev F.P. Numerical methods for solving extremal problems. – M.: Nauka, 1988. – P 552.
2. Lebedev K.A. A method of finding the initial approximation for Newton's method // Comp. Maths Math. Phys, 1996. – T. 36. – № 3. – P. 6 –14.
3. Karmanov V.T. Mathematical programming. : Nauka, 1986. – P 256.
4. Kantorovich L.V., Akilov G.P. Functional analysis. Nauka, 1984. – P 752.
5. Bazara M., Shetty K. Nonlinear programming. – M.: Mir, 1982. – P. 583