НОВЫЙ ПОДХОД В ТЕОРИИ ПОПЕРЕЧНЫХ МОСТИКОВ СТАЦИОНАРНО СОКРАЩАЮЩИХСЯ И РАСТЯГИВАЮЩИХСЯ МЫШЦ

Кокшенев В. Б.

Кандидат физико-математических наук, профессор физического факультета Федерального Университета Минас Жерайс, г. Бело Горизонти, Штат Минас Жерайс, Бразилия

НОВЫЙ ПОДХОД В ТЕОРИИ ПОПЕРЕЧНЫХ МОСТИКОВ СТАЦИОНАРНО СОКРАЩАЮЩИХСЯ И РАСТЯГИВАЮЩИХСЯ МЫШЦ

Аннотация

Несмотря на достаточно широкое применение в биомеханике, модель скользящих нитей, предложенная Хаксли, не позволяет описать поведение активированных скелетных мышц в условиях стационарного растяжения. В настоящей статье впервые предложено новое самосогласованное решение фундаментального кинетического уравнения Хаксли для распределения актино–миозиновых ниточных связей (тянуще–тормозящих поперечных мостиков) в рамках обобщенной термо– динамической теории флуктуаций. Тем самым модифицирован традиционный подход, представляющий собой упрощенный расчет частот образования и разрыва мостиков на основе теории переходных состояний. Предложено обобщенное выражение для мышечного усилия, пригодное как для состояния сжатия, так и для растяжения мышцы. Единый механизм сокращения мышцы интерпретируется взаимодействием между головками миозина, связанными c нитями актина, находящимися в термодинамически равновесных состояниях, и вращающимися неуравновновешенными головками миозина, находящимися в ассиметрично распределенных, локально равновесных состояниях. Переход от стационарного режима активного сокращения к активному удлинению мышцы объясняется реконструкцией поперечных мостиков и изменением частоты их образования и разрыва при сохранении основных упругих характеристик мостиков. Предлагается обобщенное уравнение состояния «сила–скорость» с использованием лишь одного подгоночного параметра в каждом из режимов генерации силы, в то время как в подходе Хаксли (1957) и его последующих модификациях требуется четыре параметра для описания экпериментальных данных для каждого режима актуации.  

Ключевые слова: мышечное сокращение, уравнения состояния, cтатистическая механика, теория скользящих нитей, соотношения «сила–скорость».

Kokshenev V.B.

Ph. D,  Professor,  Physics Department of the Federal University of Minas Gerais,  Belo Horizonte, Brazil, valery@fisica.ufmg.br

NEW INSIGHTS INTO THE THEORY OF CROSS-BRIDGE TENSION OF STEADILY SHORTENING AND STRETCHING MUSCLES

Abstract

Despite the great success, seminal Huxley's sliding filament model broadly fails to explain the steady state behavior of stretched activated skeletal muscles. Here, a new self-consistent solution to the fundamental kinetic equation for the distribution of actin-myosin linkages (cross-bridges) is proposed in light of the generalized thermodynamic theory of fluctuations, thus substituting the transition state theory traditionally used for the transition rates. The unified description for mechanism of the force output in both shortening and stretching regimes is attributed to the interplay between the uniformly-state distributed, thermodynamically equilibrated myosin heads attached to actin filaments and asymmetrically-state distributed, mechanically equilibrated rotating myosin heads. The crossover between two steady regimes is associated with a reconstruction of the cross-bridge domains and change their attach-detach rates, leaving unchanged basic mechanical characteristics. Theory suggests a unified generic force-velocity equation, using only a single combination of the cross-bridge parameters for each regime, while Huxley's approach (1957) as well as its subsequent modifications, requires four adjustable parameters to fit the same data.

Keywords: muscle contraction, equations of state, statistical mechanics, sliding filament theory, force-velocity relations.                  

Introduction

The early studies of muscle fibers under the light microscope revealed cross-striations running normal to the fiber axis during concentric and eccentric muscle contractions and two researcher groups [13, 14] laid the foundations for the sliding filament theory. They simultaneously suggested that muscle contractions occur due to the relative sliding of the thick myosin filaments past the thin rigid actin filaments, mediated by the ATP-dependent elastic actin-myosin linkages (cross-bridges, CBs) [13], working as independent force generators [14].

Based on the idea of the existence of mechanical equilibrium of elastic myosin molecules at the regular sites of relatively rigid actin filaments, A.F. Huxley explained the mechanism of generation of elastic muscle force via strain variation of myosin heads bound to actin molecules [15], resulting in lever-arm picture [16]. However, in spite of the great success in illuminating the force generation and power liberation during muscle shortening [15], Huxley's seminal approach generally failed to describe the ascending branch of the force-velocity curve established phenomenologically for the steady muscle lengthening. Considerable efforts have been therefore made to find an exact numerical solution to the partial differential equation [15] via ad hoc modifications of the rate functions [3, 9, 36, 37], including an arbitrary rate-velocity dependence provided the "exact" steady state solutions [3]. All such modifications explored the fact that the sliding filament model [15] leaves a free choice of the load-dependent attachment and detachment rate functions with respect of CB strains. Many researchers simulated numerically a range of muscle properties by fitting empirical data on the muscle tension in lengthening by adopting either linear-strain functions or constants [21, 22, 35], or their appropriate combinations [4, 15, 38]. Moreover, the linear-strain exponential rate functions, also suggested by Huxley [15], were either extended [23, 26] or simply substituted [29, 30] by the bilinear-strain exponential functions.

An extension of the number of adjustable parameters in sliding filament models via arbitrary chosen rate functions does not improve our knowledge on the nature of muscle force generation, thus many physical inconsistencies of modified Huxley's models were reported. For example, the requirement to Huxley's CBs to be attached at long distances during steadily muscle stretching was found as unreasonable [9], when studied within the scope of the distribution moment model by Zahalak [38], employed recently in [35]. Thereby, the central question was raised on the existence of Huxley's CBs, favoring myosin head attachment events at large displacements with the increase in contraction velocity. Likewise [9], controversies surrounding Huxley's approach were brought forth in careful studies of the force exposed by a single CB during lengthening [24].

Treating the sliding filament model by Huxley as an incomplete one, further generalizations over many-step mechanochemical myosin cycle, relating the kinetic rate constants with the standard Gibbs energies of actin-myosin states, were proposed in [6, 8, 11, 12, 16, 22, 29-31, 36]. Given that the employed transition state theory treats i) the entire system to be in a global thermodynamic equilibrium and ii) all CB degrees of freedom as being in ergodic states, such a simplified combination of the equilibrated chemical thermodynamics and mechanically equilibrated muscle dynamics seems to be rather dubious.

The approach developed in this study employs a general tendency towards establishing the thermodynamic equilibrium between all CB states, getting some of states out of the equilibrium. The treatment of statistically random strain-dependent CB states on the basis of the general theory of fluctuations removes the aforesaid uncertainties of the transition rate functions. A new analytical solution to the standard kinetic equation of the sliding filament model by Huxley [15] is proposed in the form unifying mechanisms of the force generation during both regimes of muscle contractions.

THEORY

Huxley's approach revisited

At a fixed muscle contraction velocity V, the occupation number  of CB states, combining in time t myosin filament with actin filament of the total number of sites N, obeys the common "balance" kinetic equation

\[\frac{d}{dt}{{N}_{V}}(x,t)=\frac{\partial {{N}_{V}}}{\partial t}+\frac{\partial {{N}_{V}}}{\partial x}\cdot \frac{dx}{dt}=f(x)(N-{{N}_{V}})-g(x){{N}_{V}}.\] (1)

Here f(x) and g(x) are attachment and detachment rates of the bound state located at a displacement (strain) x estimated from the actin filament site x=0 equilibrated by CB elastic energy. The steady state N_v(x,∞), achieved on practice by late times t » f⁻¹, g⁻¹ provided _∂Nv(x,t)/∂t=0 in equation (1) reduces it to the fundamental equation (4) in [15], namely

\[-\frac{V}{2}\frac{d}{dx}{{n}_{V}}(x)=f(x)(1-{{n}_{V}})-g(x){{n}_{V}},\]   (2)

suggested for CB steady-state occupation probability n_v(x)=N_v(x,∞)/N called by CB proportion [15]. According to Huxley [15], the CB force output is generated when x decreases at a positive velocity of sliding of the actin filament V_A and a negative velocity of myosin filament V_M, i.e. V_A=-V_M=-dx/dt>0. The contraction velocity per one-half sarcomere V/2 determines the contraction velocity V of the muscle as a whole, when modeled by V=V_A-V_M=2V_A. As can be derived from Huxley's equation (6) in [15] with in part preservation of his notations, the overall generated force

\[F_{V}^{(total)}=\underset{L\to \infty }{\mathop{\lim }}\,\frac{s{{N}^{'}}}{L}\int_{-L}^{+L}{F(x){{n}_{V}}(x)\frac{dx}{2{{l}_{A}}}}\]  (3)

was evaluated via the force per one myosin site, as one actin site is carried past it. Here s is the sarcomere length, ^l_A is the trial distance between the nearest sites in the actin filament evaluated in equation (15) in [15], and N′ is the number of sites in the thick filament in the overlapping zone of length L.

The solution to the steady equation (2) for the shortening regime (hereafter distinguished by index 1) was proposed as a combination of the localized (short-range) and delocalized (large-range) bound sub-states located respectively in positive and negative domains. The corresponding CB proportions, namely

\[n_{V}^{(loc)}(x)={{n}_{01}}\left( 1-\exp \left[ \frac{{{V}_{1}}}{V}\left( \frac{{{x}^{2}}}{{{h}^{2}}}-1 \right) \right] \right),\text{   }0\le x\le h\]  (4) and

\[n_{V}^{(deloc)}(x)={{n}_{01}}\left[ 1-\exp \left( -\frac{{{V}_{1}}}{V} \right) \right]\exp \left( 2x\frac{g_{1}^{'}}{V} \right),\text{   }-\infty <x\le 0,\]  (5)

are reproduced exactly from (7) and (8) in [15] and parameterized here by

\[{{n}_{01}}=\frac{{{f}_{1}}}{{{f}_{1}}+{{g}_{1}}}\text{   and   }{{V}_{1}}=h({{f}_{1}}+{{g}_{1}}).\]  (6)

In turn, this description of the two CB sub-states follows from the rates postulated by linear functions, namely

\[f(x)={{f}_{1}}\frac{x}{h}\text{   and   }g(x)={{g}_{1}}\frac{x}{h},\text{   for }0\le x\le {{x}_{1}}=h,\]  (7)

and two piecewise constants f′(x)=0, g′(x)=g₁′, for -∞<x<0. The muscle concentric steady force F_V^(short) reduced to the isometric force F₀ found on the basis of (3)-(7), namely

\[\frac{F_{V}^{(short)}}{{{F}_{0}}}=1-\frac{V}{{{V}_{1}}}\left[ 1-\exp \left( -\frac{{{V}_{1}}}{V} \right) \right]\left( 1+\frac{V{{V}_{1}}}{2{{h}^{2}}g_{1}^{'2}} \right),\text{   for }V>0,\]  (8)

was fitted in [15] by the four CB kinetic parameters: f₁ = 43.3 s⁻¹, g₁ = 10.0 s⁻¹, f₁′ = 0 , and g₁′ =209 s⁻¹. In addition, two more adjustable parameters h≈15 nm and V₁=V^(exp)_max/4, where V^(exp)_max is the empirical maximum shortening velocity, were directly and indirectly employed when tested by Hill's empirical equation [10] (for details, see chapter IV in [15]). It is noteworthy that the nearest-site distance in the actin filament treated as a free parameter was estimated as l≈h, i.e. close to the known nearest-molecular distance in the myosin filament l_M=14.5 nm [5]. However, the ratio F_-∞ ^(stret)/F₀=(f₁+g₁)/g₁=5.33 reported by Huxley [15] for the muscle lengthening regime, contrasts to the observed ratios falling between 1.8 and 2.0 (see e.g. [9, 14, 26]).

A new solution to the fundamental kinetic equation

Beyond any specific suggestions, the formal solution to the steady-state equation (2):

\[{{n}_{V}}(x)={{n}_{0}}(x)+\Delta {{n}_{V}}(x)={{n}_{0}}+(1-{{n}_{0}}){{c}_{V}}\exp \left( -\frac{1}{{\dot{x}}}\int_{0}^{x}{[f({x}')+g({x}')]d{x}'} \right),\dot{x}\equiv \frac{dx}{dt}=\mp \frac{V}{2},\] (9)

is valid for any contraction shortening velocity V (= - 2 > 0) and lengthening velocity V (=2x<0), leaving arbitrary a choice of the rate functions f(x) and g(x). The first order differential equation possesses, as common, has only one free constant (denoted in (9) by c_V), whereas another one, namely

\[{{n}_{0}}(x)=\frac{f(x)}{f(x)+g(x)},\]  (10)

controlled by muscle e intrinsic rates, straightforwardly follows from (2) taken at V = 0. One can see that in Huxley's version of (9) the constant c_V=-n₀₁(1-n₀₁)^-1exp(-V₁/V) results from the periodic boundary condition  n_V(h)=0, providing the non-Gaussian CB proportion shown in (4).

Besides the boundary conditions re-considered below, the property of periodicity in the overlapping part of the actin filament of total length Nd, should be taken into consideration. Moreover, as noticed by Hill et al. ([12], p. 346]), the quantity n_V(x)dx has a meaning of the late-time probability to find one of the two myosin heads in the bound state within the domain [x , x + dx]. Consequently, the total force output in the finite-range overlapped zone is

\[F_{V}^{(zone)}=\int_{-Nd}^{+Nd}{F({x}'){{n}_{V}}({x}')\frac{d{x}'}{2d}=N}\int_{-d}^{d}{F(x){{n}_{V}}(x)\frac{dx}{2d},\text{   where }{x}'=xN.}\]   (11)

Here F(x) is the active force per one actin cell, substituting that in (3) estimated per one myosin site. Such a consideration suggests the statistical equivalence of all the occupied cells in the actin filament treated as a one-dimensional crystal of the lattice constant d. If one takes into account that the sum of strain-dependent occupation numbers N_V(x,∞) of the one-molecule steady states x is limited by the total number N of available actin filament sites, the following normalization condition, namely

\[\int_{-d}^{+d}{{{n}_{V}}(x)\frac{dx}{2d}=}\int_{0}^{d}{{{n}_{V}}(x)\frac{dx}{d}=\int_{-d}^{0}{{{n}_{V}}(x)\frac{dx}{d}=}1,}\]   (12)

constraining the CB occupation probability, should be applied. Such a normalization is consistent with (3) and (11).

It was proposed by T. L. Hill [11] to extend Huxley's idea on the minimum of CB elastic energy at x = 0 over the minimum of Gibbs energy [8, 12]. More generally, one deals with a thermodynamic system associated with the electrically activated, loaded muscle and mechanically equilibrated system steadily contracting a fixed temperature.

Having the configurational entropy S_V(x), a given CB contracting at the velocity V tends towards the global equilibrium characterized by the maximum S_V(0). The mean of a random strain x of the bound myosin molecule is treated as the thermodynamic quantity, linear with the generated force (see e.g. equations (3) and (16) below), where the x-state probability n_V(x) is proportional to exp(S_V(x)). The latter is due to Boltzmann's principle stating that the logarithm of the probability of fluctuations is proportional to its entropy, introduced by Einstein in 1910 as the methodological foundation for the fluctuation theory [20, 25]. As common, the fluctuation part of the entropy ΔS_V(x)=S_V(x)-S_V(0) can be related to the negative minimum work required to bring the given CB from a certain non-equilibrated state, associated with x strain, to the "true equilibrium state" at x = 0 under interaction with the rest of the whole system. Taking into account the maximum of entropy at x = 0, the first derivative of S_V(x) is zero and the second derivative is negative that yields the Gaussian form for n_V(x), centered at x = 0.

One can see that the requirement on n_V(x) to be Gaussian can be satisfied in (9) solely by the linear parameterization of the rate functions, namely

\[f(x)={{f}_{m}}\frac{x}{{{x}_{m}}},\text{ }g(x)={{g}_{m}}\frac{x}{{{x}_{m}}},\text{ for }{{x}_{m}}={{x}_{+}}\ge x\ge 0\text{ or }{{x}_{m}}={{x}_{-}}\le x\le 0.\]     (13)

The shown positive and negative domains [0,x_m] arise from the velocity-displacement-sign agreement  xx>0, also required by the Gaussian form. Finally, the normalization constant in equation (9)

\[{{c}_{V}}=\frac{d}{\left| {{x}_{m}} \right|}\frac{2}{\sqrt{\pi \upsilon }}erf{{\left( \frac{1}{\sqrt{\upsilon }} \right)}^{-1}},\text{   with }\upsilon =\frac{V}{{{V}_{m}}}=\frac{2\dot{x}}{({{f}_{m}}+{{g}_{m}}){{x}_{m}}}>0,\]  (14)

readily follows from the normalization condition discussed in (12). In (14), the standard error function , acting within the domain [erf(0)=o,erf(∞)=1], is employed.

Boundary conditions

The periodic boundary conditions for CB states should be additionally applied to the solution of (2), thereby introducing additional correlations and reducing the number of independent parameters. As seen in (9), a new solution generic for both steady regimes is composed of the static state occupied with n₀(x)=f_m/(f_m+g_m), following from (10) and (13), and the dynamic state with Δn_V(x), disappearing in the static limit V→ ± 0 at any finite x located either in positive (d≥x₊≥x≥0) or (-d≥-x_-≥x≥0) negative strain domains described in (13). The static CB states are generally permitted to exist in a positive domain 0≤x≤x₀ or a negative -x₀≤x≤0 domain determined by the new CB structure parameter x₀(≤d). The dynamic-state domain limitations arise from the mechanical constraints discussed below.

Bearing in mind that the positivity of the velocity V^(short)=V_A-V_M=-2x, in shortening regime, and the negativity of the stretching velocity V^(short)=V_A-V_M=2x

(see text below equation (9)) are constrained by the requirement xx>0, one infers that the only negative domains are mechanically available for the CB dynamic states. The provided analysis summarized in the trial (9) yields

\[{{n}_{V}}(x)={{n}_{0}}{{\Theta }_{0}}(x)+(1-{{n}_{0}}\frac{{{x}_{0}}}{d})\frac{d}{{{x}_{-}}}\frac{2}{\sqrt{\pi \upsilon }}\frac{\exp \left( -\frac{{{x}^{2}}}{\upsilon x_{m}^{2}} \right)}{erf\left( \frac{1}{\sqrt{\upsilon }} \right)}{{\Theta }_{V}}(x)\]        (15)

obtained with the help of (14). The discussed above boundary conditions now are incorporated into the novel solution to Huxley's model via the "static-state" Θ₀(x) and "dynamic-state" Θ_V(x) auxiliary  functions, specifying the CB domains via the standard Heaviside (step) function Θ(y). Specifically, Θ(y) is one for y ≥ 0 and zero for y <0; Θ₀(x)=Θ(x)-Θ(x-x₀), for the positive-strain CB domain; Θ₀(x)=Θ(x)-Θ(x+x₀) and Θ_V(x)=Θ(-x)-Θ(x+x_-), for negative domains.

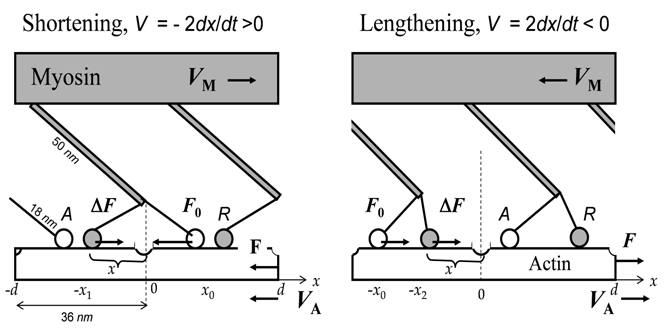
In Fig.1, possible CB domains, simultaneously allowed by kinetics and thermodynamics for the dynamic-state fluctuations near the equilibrated static states, are shown along with the self-consistent mechanical constraints imposed on directions of the force output and sliding filament velocities.

RESULTS

Muscle force

The mean force produced by one CB occupied in a periodic cell of the actin filament

\[F_{V}^{(cell)}={{F}_{0}}+\Delta {{F}_{V}}=k\int_{-d}^{+d}{x{{n}_{V}}(x)\frac{dx}{2d}=}{{F}_{0}}-k\frac{{{x}_{-}}}{2}(1-{{n}_{0}}\frac{{{x}_{0}}}{d})\Phi (\upsilon ),\text{ }{{F}_{0}}=\pm \frac{kx_{0}^{2}}{2d}{{n}_{0}},\]  (16)

is calculated using (11) and (15) on the basis of the CB stiffness k=F(x)/x[15, 16], velocity-independent intrinsic muscle quantity, e.g. [14]. The static part F₀ is found to be positive during shortening regime and negative during stretching regime, as demonstrated in Fig. 1. The negative-domain dynamic part ΔF_V is linear with the universal dynamic function

Fig. 1. A mechanical scheme of the steady force generation by the bound actin-myosin linkages resulting from (15) and (16). Each of the two equivalent myosin heads of the effective CB may be bound with the actin filament stationary or dynamically, forming respectively the equilibrated attached state A (shown by the open circle) within domains [0 , ± x₀] or the non-equilibrium steady dynamic rotated state R (closed circle), within the negative domains [0 , -x₁₋] and [0 , -x₂₋], shown respectively for the muscle shortening and stretching. The arrows indicate directions of the sliding velocity of the actin filament  and the myosin filament. 

 \[\Phi (\upsilon )=2\sqrt{\frac{\upsilon }{\pi }}\frac{1-\exp \left( -\frac{1}{\upsilon } \right)}{erf\left( \frac{1}{\sqrt{\upsilon }} \right)};\text{   with }\Phi (0)=0,\text{ }\Phi (1)=0.486,\text{ and }\Phi (\infty )=1,\]    (17)

where the scaling positive parameter  is defined in (14). In this way, a unique equation

\[\frac{{{F}_{V}}}{{{F}_{0}}}=1\mp {{\sigma }_{m}}\Phi (\upsilon ),\text{   with }{{\sigma }_{m}}=\frac{(d-{{n}_{0}}{{x}_{0}}){{x}_{-}}}{{{n}_{0}}x_{0}^{2}},\]      (18)

substituting Huxley's model (8), is proposed for the CB force output reduced to CB isometric force F₀, unifying both concentric (the case of negative sign in equation (18)) and eccentric (positive sign in equation (18)) muscle contractions driven respectively by the positive and negative steady velocities V=υV_m. Below, the one-parameter fitting analysis of the proposed theory is conducted on the basis of known experimental data on muscle force.

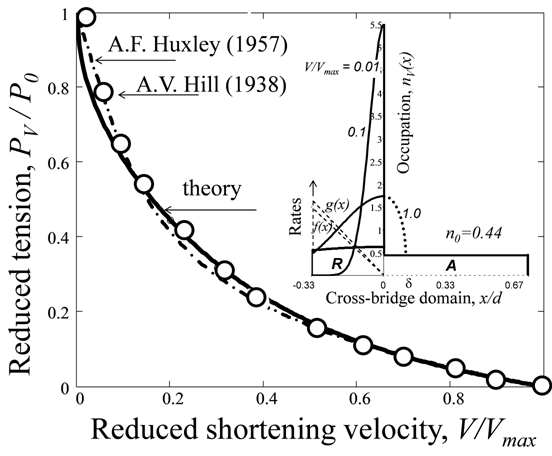
Fig. 2. Analysis of the force-velocity branch predicted for the steady muscle shortening. The points and dashed-point curve are Hill's empirical data [10] shown in (22) and those fitted by Huxley's curve discussed in (8). The solid line is (19) that fits Hill's data at λ = 0.85. Inset: The reduced CB occupation numbers modeled in the Appendix for different shortening velocities reduced to the maximum velocity (shown by solid lines) and the corresponding attach and detach rates (dashed lines). The dotted line schematically drawn for indicates a correction due to the possible dynamic-static (R-A) transient state discussed in the Discussion.

In Fig. 2, the tension-velocity data on steady shortening muscle are described by the equivalent equation  following from (18), namely

\[\frac{F_{V}^{(short)}}{{{F}_{0}}}\equiv \frac{P_{V}^{(short)}}{{{P}_{0}}}=1-\frac{\Phi \left( \lambda V/{{V}_{\max 1}} \right)}{\Phi (\lambda )},\text{ }0\le V\le {{V}_{\max 1}},\text{ }{{V}_{\max 1}}=\lambda {{V}_{m1}},\text{ }{{V}_{m1}}={{x}_{1-}}({{f}_{1-}}+{{g}_{1-}}).\]   (19)

Here, the well known property of the zero force at the maximum velocity V_max is employed to relate V^(exp)_max with the characteristic CB velocity V_ml specified in (19), through a new auxiliary parameter λ. The two adjustable parameters in the equivalent (18) and (19) are connected via the universal dynamic function .

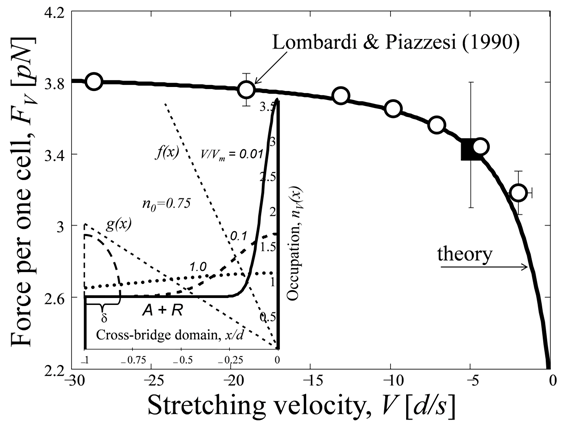
Fig. 3. The steady force output by one cross-bridge occupying one cell of the actin filament versus the stretching velocity. The open circles are the mean datapoints of the forces (re-scaled by  pN) measured by Lombardi and Piazzesi in frog muscle fibers maintained at 50⁰C and negative velocities, lying between 75 and 1030 nm/s (see Fig. 7 in [14]), scaled here by d = 36 nm. The closed square indicates the force per one CB reported in [24] for unspecified velocity. The theoretical curve is drawn via (20) taken at . Inset: The CB reduced occupation numbers (solid, dotted and dashed lines) and attach-detach rates (dashed lines) predicted for three distinct velocities reduced to the characteristic velocity . For details, see equation (25) and Appendix. The dotted line has the meaning of that in the inset in Fig. 2.

Similarly, the data on the reduced force output are fitted in Fig. 3 by

\[\frac{F_{V}^{(stret)}}{{{F}_{0}}}=1+\Phi \left( \frac{V}{{{V}_{m2}}} \right),\text{ }-\infty <V\le 0,\text{ }{{V}_{m2}}=-{{x}_{2-}}({{f}_{2-}}+{{g}_{2-}})<0,\]     (20)

using the characteristic negative stretching velocity V_m2  as a free parameter. For simplicity, the model parameter σ^(mod)_m2 in (18) is taken to be one in order to fit approximately the experimental data on σ^(exp)_m2 generally lying between 0.8 and 1.0, that follows from the mentioned above maximal force F_-∞. Combining results of the fitting analyses in figs. 2 and 3, one has

\[\sigma _{m1}^{(\exp )}>1\ge \sigma _{m2}^{(\exp )}.\]   (21)

The consequences of the constrains in (21) imposed on kinetic and structure CB characteristics are modeled in the Appendix and shown in the insets in Figs. 2 and 3.

DISCUSSION

Model assumptions and relation to other theories

A description of the muscle action broadly requires the synthesis of mechanical, structural and biochemical concepts. The sliding filament model determined here in the simplest form includes one mechanical parameter k, related to CB stiffness in the fully activated muscle, and four structural parameters: a number N of actin sites available, a period d of the thin filament lattice, associated with the CB domain, and two sub-domain distances x₀ and x_m. The two kinetic parameters f_m and g_m characterize the slopes of the attach and detach rate functions. The CB parameters are additionally distinguished by indexes 1 and 2, specifying the shortening and stretching muscle regimes, as well as by positive and negative signs, indicating positive-strain and negative-strain domains. As common, the longitudinal CB stiffness is adopted to be state independent, i.e. k_0±=k₁₋=k₂₋=k.

Similar to a number of studies [6, 15, 16, 29, 30, 35, 36], it is also assumed that the myosin head can bind to any point on the thin rigid filament. The found single strain-dependent actin-myosin bound state, characteristic of muscle cycling periodic steady-velocity process, emerges as a complex CB state. It effectively accounts for all possible translation-rotation CB random states, presented here by the minimal set of thermodynamic and mechanical characteristics governed by a single variable strain x. Since the occupation-number n_V(x) has the meaning of the probability of CB located within the periodic domain of actin filament it is additionally (to other researches) normalized. Moreover, the proposed a strain-state description allows to relate the occupation-state probability n_V(x) to corresponding Boltzmann's entropy S_V(x), thereby synthesizing CB thermodynamics and mechanics.

The net muscle tension would be zero, if the thermal equilibrium was possible between all CBs degrees of freedom and the surrounding thermal bath [28]. Unlike the thermal equilibrium postulated by transition state theory [6, 8, 11, 12, 16, 22, 29, 30, 36], the found actin-myosin bound state is favored solely by a trend towards the global thermal equilibrium. The attach-detach rates found on the basis theory of thermodynamic fluctuations appear to be limited by linear-strain functions, remarkably suggested by Huxley's [15]. Consequently, the complex CB state appears to be combined from the equilibrated static and non-equilibrated dynamic bound sub-states distributed respectively via the uniform n₀ and strain-dependent Δn_V(x) occupation probabilities, as shown in (9).

In order to reveal a link between the complex CB state and more realistic detail CB states, let us address the sliding filament (3G) model by Smith and Geeves [29, 30] dealing with four actin-myosin bound states: the two attached states (A-MDP and A-MT) and two rotated states (A.MDP and A.MT) called respectively by the attached A and rotated R states.

Analysis of the occupation probabilities in the shortening regime at moderate and high velocities indicates (see, respectively, Fig. 5 in [29] and Fig. 6B in [30]) that the attached and rotated states exist respectively in the negative and positive domains, in accord with our analysis shown in the inset in Fig. 2. Moreover, the overall four-state domain spreads over approximately 36 nm, the distance associated here, as well as in [12, 27, 33], with the actin filament period d (though, a distance of 38.5 nm was adopted in [29, 30] for d). One therefore arrives at more "mechanistic" treatment of the complex CB state simplified by the two-state kinetics, on the one hand, and more specific thermodynamic treatment of the A and R states oversimplified by the transition state theory, on the other hand.

Thus, mutually correlated (via occupation numbers) the static and dynamic sub-states are attributed, respectively, to the head-myosin attached, thermally (globally) equilibrated bound states and the head-myosin rotated, mechanically (locally) equilibrated bound states.

It was also suggested in [29] to use strong-binding and weak-binding states as synonymous with attached and rotated states. Moreover, the static-attached and dynamic-rotated states were independently revealed by Rayment et al. [27], via the observations "of catalytic domains of myosin being initially weakly attached to actin, and the following structural changes resulting in tight binding of actin-myosin linkages". Thereby, structural studies of force generators in contracting muscles strongly collaborate with main properties of CBs of this study obtained through the application of the second law of thermodynamics to the new static and dynamic solutions of the two-state differential equation pioneering by Huxley.

The force generation mechanism

As shown in (16), the CB force output F_V is due to the interplay between the velocity-independent force F₀ and contractive force ΔF_V produced by, respectively, static A and dynamic R sub-states. During concentric muscle contractions with a positive velocity V, the so-called isometric force F₀ is also positive, whereas the contractive force ΔF_V is negative as found in (19) and that collaborates with  the ATP hydrolysis results. During eccentric contractions, commonly associated with the negative direction of the velocity V, both the forces are also negative (see Fig. 1).

A question arises on the role of A and R states in the muscle force generation revealed by force-velocity steady behavior by other researches. Although detail analysis on the basis of the 3G model was made neither for steady muscle shortening [29] nor stretching [30], it was mentioned in [30] that A and R states are respectively responsible for the low-force and high-force output. As for Duke's model [6], it was only reported on the fitting of the data by Edman [7] on muscle steady shortening by four dimensionless combinations of model parameters, but no explicit force-velocity relation was provided or discussed.

The seminal comparative analysis of  A. F. Huxley's and A. V. Hill's data on muscle concentric tension (see [15], p. 287) is revisited in Fig. 2, where the fitted experimental data are presented by the famous  phenomenological relation [10], namely

\[\frac{P_{V}^{(\exp )}}{P_{0}^{(\exp )}}=\frac{F_{V}^{(\exp )}}{F_{0}^{(\exp )}}=a\frac{1-V/V_{\max }^{(\exp )}}{a+V/V_{\max }^{(\exp )}},\]        (22)

where a = 0.25 corresponds to the force-velocity data P^(exp)_V on the titanic stimulated shortening frog muscle at 0⁰C. The analysis of the high-velocity wing of the tension-velocity data provided with the help of (19) indicates that the attached A states, having a positive domain, control the curve above V/V_max = 0.5. This conclusion is due to the occupation probabilities of the non-equilibrated rotated states decrease with sliding velocity. Such a high-velocity behavior, shown in the inset in Fig. 2, is remarkably in agreement with the negatively located R states shown in Fig. 6B in [30]. It is noteworthy that Huxley's delocalized state determined in (5), also fits the high-velocity data by A. V. Hill [10] and Edman [7]. However, the low-velocity Hill's data within 0.2 < V/V_max < 0.5 reveal the inconsistency with Huxley's CBs (4), located in the positive domain and exerted negative force ΔF_V. As shown by current study, the CB positive-strain rotations contradict to the overall trend of achieving of maximum entropy. Consequently, instead of the retarded detachment (g₁ < f₁) of Huxley's CBs discussed in (4) and (7), the negatively dislocated rotations of myosin heads require faster detachment than attachment (g_m > f_m1) during muscle steady shortening, and slower detachment (g_m2 < f_m2 ) during muscle steady lengthening, as illustrated in the insets in Figs. 2 and 3.

As for the regular deviation of the solid line in Fig. 2 from the data at very low velocities , it can be understood by an incomplete description of the almost-equilibrated slow rotations lying in the vicinity of x ≈ 0 where R and A states overlap within the distance δ of  ≈ 5.5 nm, as seen in Fig. 5 in [29] and also in Fig. 6B in [30]. Our fit analysis of the low-velocity data could be therefore improved when the CB occupation probabilities will be locally symmetrized within the range –δ ≤ x ≤δ, as shown by the dotted line for the particular case V/V_max = 0.1 in the inset in Fig. 2. As for the discrepancy between the data by A. V. Hill [27] and Edman [7], the likely distinct experimental conditions underlying the preparation of equilibrated and non-equilibrated CB states during steady muscle shortening need further analysis.

In Fig. 3, the upper branch of the generic force-velocity curve (18) fits well the data on CB force during the stretch [29], when taken under experimental condition F^(stret)_∞=2F₀ and drawn via (20) using a single adjustable parameter V^(exp)_m2. Likewise the analysis in Fig. 2, a deviation of the theoretical curve from the data at low velocities can be improved when a certain R-A overlapping bound state is introduced, similarly to that suggested by Mehta and Herzog [24] in their Fig. 3.

Stretching against shortening

In view of the additivity of the CB force output, the provided study on the steady-state force-velocity equation (18) can be equally applied to the reduced tension due to a single CB, sarcomere, fiber, or muscle as a whole during its steady shortening or lengthening. As shown in (25) in the Appendix, the model conditions (21) of observation of the data via the universal dynamic function Φ(υ) are reduced to the inequalities n^(stret)₀>1/2>n^(short)₀, limiting occupation numbers of the attached CB states. Since n₀ = f_m / (f_m + g_m), this finding is reformulated into the aforesaid inequalities f^(short)_m<g^(short)_m and f^(stret)_m>g^(stret)_m. In contrast to Huxley-like models, see e.g. [9], this finding is supported by recent data on the cycle duty ratio β ( = 1 - n₀, the characteristic time of attachment f_m⁻¹ related to total CB cycling time f_m⁻¹+ g_m⁻¹) [24] generally indicating that β_stret < β_short (see table 1 in [24]). Therefore, one can extend the above inequalities to

\[g_{m}^{(short)}>f_{m}^{(short)}>f_{m}^{(stret)}>g_{m}^{(stret)},\]   (23)

in accord with the insets in Figs. 2 and 3. Such a hierarchy of the rates established for the new CBs corroborates the working hypothesis in [24] on "that a stretched cross-bridge might remain attached longer than a cross-bridge that had been shortened while attached", i.e. g^(stret)-1_m>g^(short)-1_m.

As may be expected, this deduction conflicts with the conclusion that the "reattachment (in steady lengthening is)... faster than attachment in the isometric condition or during shortening" [14], one of the major results obtained in [14] on the basis of Huxley's (4) and (5). A crossover between the stretching and shortening muscle regimes is shown to be due to a reconstruction of the bound sub-states, including structural domains and exchange kinetic parameters, leaving unchanged the mechanical CB characteristics.

Implications of the approach

In spite of revealed by different researches inconsistencies  of Huxley's CBs with the experimental data on both muscle steady shortening and stretching, one can see that the major mechanical concept on the CB compliance [15] remains to be common to all modern sliding filament models. The incorporation of conformational changes of myosin molecules into the two-state model [15] improved kinetic cycle by multiple CB states [6, 14, 21, 22, 29, 30, 35], characteristic of real striated and smooth muscles. Further generalization of the rigid sliding filament model [15] over tropomyosin deformations resulted in strong correlations between originally "independent force generators" [14]. The corresponding incorporation of the filament compliance resulted in the effect of cooperatively in CB tension production, now understood at both molecular and macroscopic levels of consideration, i.e. via the filament crystal-like periodicity, e.g. [21], and through the elastic continues medium, e.g. [31].

In the same context, a simplified consideration for the complex, attached-and-rotated CB state, propagating along periodic actin filament lattice of period d = 36 nm [10, 27, 33] is considered here in the continues-strain approximation, likewise the studies [6, 8, 11, 12, 14-16, 26, 29, 30, 36, 38], naturally excluding the so-called "target zones", favorably oriented sites on the helices of the actin filament separated by distances of about 5.5 nm [21, 33], 11 nm [21, 34], or 36 nm [21, 33]. One can see that unlike the target-zone domains, associated with certain load-dependent bound sub-states, ultimately determining the preferable step distance [21], the load-independent distance d plays the role of an external parameter, that may scale structural, mechanical and dynamic characteristics, as shown in (18). Given that the force-velocity steady muscle behavior is not affected directly by variations of the structural or energetic parameters, a new additional domain activated during stretching in the myosin filament [1] can be readily included.

The utility of the proposed improvement of the simplest sliding filament model may be also clarified by the fact that any temporal non-steady muscular behavior, including residual force effects [35], is underlaid by the steady-state solutions to kinetic equations [3, 14, 26, 35]. The principal suggestion, differing the current study from other analytical approaches explaining the force production during muscle shortening [6, 12, 22, 24, 30] and stretching [29, 30], is that instead of the thermally equilibrated CB states postulated by the transition-state theory, it is adopted here that not all of them are allowed to be in thermal equilibrium. According to the generalized fluctuation theory [17, 20, 25], directly exploring the second law of thermodynamics, the configurational part of the entropy drives the muscle loaded system towards the global equilibrium throughout the locally equilibrated CB rotated states. As the result, the mechanically-equilibrated rotations of  S1 myosins, attaching and detaching via linear-strain-dependent rates, are predicted to be distributed via the symmetric Gaussian form. The existence of such dynamic rotations located in the negative-strain CB domains is revealed here via both branches of the generic force-velocity curve. The extension of the proposed approach on the specific-state transient CB kinetics will not affect the overall-state domain and therefore the general picture of force generation.

Another prediction, challenging further experimental verification, is that the entropy production during the steady stretching regime is lower than that during shortening regime. This finding arises from the constraint imposed on the mean numbers for the rotated states, i.e. Δn^(stret)_V>Δn^(short)_V, opposing the case of the attached static states. Thereby, a reduction of the energy consumption during lengthening can be understood within the same framework, excluding a speculation about the existence of two distinct mechanisms for muscle steady shortening and steady lengthening, as initially suggested by Huxley ([15], p. 292) and then modeled by Lombardi and Piazzesi [14, 26].

Alternative approach in the framework of the sliding filament has been recently proposed Shilko and co-workers in [2] and developed in [28]. On the basis of the application of Huxley’s kinetic equations to pulling and braking cross-bridges, the stationary solutions for the mean statistical occupation numbers of bridges was obtained [2], leading to the phenomenological Hill equation and thus revealing the origin of equation (22) and its free parameters at a molecular level. As a next step, it is interesting to test the proposed model for experimental data for the muscles during steady elongation and thereby to generalize the same Hill`s equation for the phase of muscular stretching.

CONCLUSION

The provided study clearly demonstrates how the force response to external loads, emerging in the steadily shortening or stretching muscle, yields universal correlations between mechanical, structural and kinetic model muscle characteristics, when rationalized in light of the fundamental law of thermodynamics. Likewise, the correlations caused by accommodation of the generated force to distinct patterns of external loads during efficient eccentric, isometric, or concentric contractions were revealed in terms of the primary locomotor muscle functions via the most general laws of the theory of elasticity [18,19].

Acknowledgements

The author is grateful Scott Medler for helpful comments.

APPENDIX

Modeling CB domains

The inequalities shown in (21) following from the fitting analysis provided in figs. 2 and 3 are now specified by

\[{{n}_{01}}<\frac{{{x}_{1-}}d}{{{x}_{01}}({{x}_{01}}+{{x}_{1-}})}\text{ and }{{n}_{02}}>\frac{{{x}_{2-}}d}{{{x}_{02-}}({{x}_{02-}}+{{x}_{2-}})}\]    (24)

with the help of (18), where negative signs indicate negative CB-strain domains. Then, additional geometrical constraints x₁₋< d / 2 and x₂₋ < d, corresponding to the fact that the tail of the myosin molecules is longer than heads (see Fig. 1), generally results in x₂₋ > x₁₋, thereby providing n₀₂ > n₀₁ in (24). If a simplified model requirement of periodicity of CB states x^(mod)₀₁+x^(mod)_1- is also adopted, along with a condition of the coexistence of the sub-states (e.g. x^(mod)_02-=x^(mod)_2-=d, one has the  requirement

\[n_{02-}^{(\bmod )}\ge 1/2>n_{01}^{(\bmod )},\]    (25)

For the case of muscle shortening, the chosen CB structure parameters are x^(mod)₀₁=2d/3  and x^(mod)_1-=d/3, which in combination with the fitting parameter σ^(exp)_ml=1.22 shown in (18) specify the numbers n^(mod)₀₁=0.44 and n^(mod)_V(x) for the static (attached A) and dynamic (rotated R) states illustrated in the inset in Fig. 2. Moreover, when the maximum velocity V^(exp)_max1=3200 nm/s for the experimental data analyzed in Fig. 2 is employed, the model attachment and detachment rates f^(mod)_1-=138s⁻¹ and g^(mod)_1-=176s⁻¹ are straightforwardly follow from the relations f₁₋=V_max1 n₀₁/λx₁₋ and g₁₋=f₁₋(1-n₀₁)/n₀₁ provided by (9), (10), and (19).

For the case of activated muscle stretching, the fitting analysis in Fig. 3 provides V^(exp)_m2= - 288 nm/s). In the inset in Fig. 3, the used estimate n^(mod)_02-=0.75 for the static-state occupation data is obtained with the help of the relation n₀₂₋ = f₂₋x₂₋ / |V_m2|, following from (10) and (20), where (f₂₋)⁻¹ is associated with the characteristic dwell time for the CB attachment found about 0.167 s [24]. Such a simplified modeling provides the model data f^(mod)_2-=6s⁻¹ and g^(mod)_2-=2s⁻¹ estimated via g₂₋=f₂₋(1 - n₀₂₋) / n₀₂₋ and illustrated in the inset in Fig. 3.

References

1. Brunello E., Reconditi M., Elangovan R., Linari M., Sun Y.B., Narayanan T., Panine P., Piazzesi G., Irving M., Lombardi V. Skeletal muscle resists stretch by rapid binding of the second motor domain of myosin to actin // Proc. Natl. Acad. Sci. USA. – 2007. – No 50. – P. 20114–20119.
2. Chernous D. A., Shilko S. V. Modelling of contractive activity of the muscle tissue // Russian Journal of Biomechanics. – 2006. ­– No. 3. – P. 51-60.
3. Chin L., Yue P., Feng J. J., Seow C.Y. Mathematical simulation of muscle cross-bridge cycle and force-velocity relationship // Biophys. J. – 2006. – No 10. – P. 3653 –3663.
4. Cole G.K., Bogert A.J., Herzog W., Gerritsen K.G. M. Modelling of force production in skeletal muscle undergoing stretch // J. Biomech. – 1996. – No 8. – P. 1091-1104.
5. Craig R., Woodhead J. L. Structure and function of myosin filaments // Curr. Opin. Struc. Biol. –2006­.– No 2. – P. 204–212.
6. Duke T. A. J. Molecular model of muscle contraction // Proc. Natl. Acad. Sci. ­ USA – 1999.­ – No 6. – P. 2770–2775.
7. Edman K. A. P. Double-hyperbolic force-velocity relation in frog muscle fibres // J. Physiol. – 1988.– No 10. – P. 301–321.
8. Eisenberg E, Hill T. L., Chen Y. D. Cross-bridge model of muscle contraction. Quantitative analysis // Biophys. J. – 1980.– No 2. – P. 195 –227.
9. Harry J. D., Ward A. W., Heglund N. C., Morgan D. L., McMahon T. A. Cross-bridge cycling theories cannot explain high-velocity lengthening behavior in frog muscle // Biophys. J. – 1990.– No2. – P. 201–208.
10. Hill A.V. The heat of shortening and the dynamic constants of muscle // Proc. Royal Soc. London – 1938.– No 843. – P. 136–195.
11. Hill T. L. Theoretical formalism for the sliding filament model of contraction of striated muscle, part I. // Prog. Biophys. Molec. Biol. –1974.–P. 267–340.
12. Hill T. L., Eisenberg E., Chen Y., Podolsky R. J. Some self-consistent two-state sliding filament models of muscle contraction // Biophys. J. – 1975. – P. 335–372.
13. Huxley H. E., Hanson J. Changes in the cross-striations of muscle during contraction and stretch and their structural interpretation // Nature – 1954.– No 4412. – P. 973–976.
14. Huxley A. F., Niedergerke R. Interefrenec microscopy of living muscle fibres // Nature – 1954.– No 4412. – P. 971–973.
15. Huxley A. F. Muscle structure and theories of contraction // Prog. Biophys. Biophys. Chem. – 1957.– No 7, – P. 255–318.
16. Huxley A.F., Simmons R.M. Proposed mechanism of force generation in striated muscle Nature – 1971.– No 5321. – P. 533–538.
17. Kestin J., Dorfman R. A course in statistical thermodynamics . – New York, San Francisco: Academic Press, 1971.
18. Kokshenev V. B. A force-similarity model of the activated muscle is able to predict primary locomotor functions // J. Biomech. – 2008.– No 4. – P. 912–915.
19. Kokshenev V. B., Modeling mechanical patterns for striated muscles // J. Biomedical Science and Engineering, – 2014.– No 8. – P. 473–496.
20. Landau L. D., Lifshitz E. M. Statistical Physics, third ed. – London: Pergamon Press, 1989.
21. Lan G., Sun S. X. Flexible light-chain and helical structure of F-actin explain the movement and step size of myosin-VI // Biophys. J. – 2006.– No 11. – P. 4002–4013.
22. Lan G., Sun S.X. Dynamics of myosin-drive skeletal muscle contraction: I. steady-state force generation // Biophys. J. – 2005.– No 6. – P. 4107–4117.
23. Lombardi V., Piazzesi G. The contractile response during steady lengthening of stimulated frog muscle fibres J. Physiol. – 1990.– No 12. – P. 141–171.
24. Mehta A., Herzog W. Cross-bridge induced force enhancement? // J. Biomech. – 2008.– No 7. – P. 1611–1615.
25. Onsager L., Machlup S. Fluctuations and irreversible processes // Phys. Rev. – 1953.– No 6. – P. 1505–1512.
26. Piazzesi G., Francini F., Linary M., Lombardi V. Tension transients during lengthening of tetanized muscle fibre of the frog // J. Physiol. – 1992.– No 1. – P. 659–771.
27. Rayment I., Holden H. M., Whittaker M., Yohn C. B., Lorenz M., Holmes K. C., Milligan R. A. Structure of the actin-myosin complex and its implications for muscle contraction // Science – 1993.– No 5117. – P. 58–65.
28. Shilko S. V., Chernous D. A., Pleskachevsky Yu. M. Nonlinear deformation of skeletal muscles in a passive state and in isotonic contraction // Mechanics of Composite Materials. – 2012. – No 3. – P. 331–342.
29. Smith D. A., Geeves M. A. Strain-dependent cross-bridge cycle for muscle // Biophys. J. – 1995.– No 2. – P. 524–537.
30. Smith D. A., Geeves M. A. Strain-dependent cross-bridge cycle for muscle I. Steady-state behavior // Biophys. J. – 1995.– No 2. – P. 538–552.
31. Smith D. A., Maytum R., Geeves M. A. Cooperative regulation of myosin-activation interactions by a continuous flexible chain I: Actin-tropomyosin systems // Biophys. J. – 2003.– No 5. – P. 3155–3167.
32. Smith D. A., Geeves M. A. Cooperative regulation of myosin-activation regulations by a continuous actin-tropomyosin-troponin and regulation by calcium // Biophys. J. – 2003.– No 5. – P. 3168–3180.
33. Steffen W., Smith D., Simmons R., Sleep J. Mapping the actin filament with myosin // Proc. Natl. Acad. Sci. USA – 2001.– No 26. – P. 14949–14954.
34. Veigel C., Molloy J. E., Schmitz S., Kendrick-Jones J. Load-dependent kinetics of force production by smooth muscle myosin measured with optical tweezers // Nature Cell Biol. – 2003.– No 11. – P. 980–986.
35. Walcott S., Herzog W. Modeling residual force enhancement with generic cross-bridge models // Math. Biosci. – 2008.– No 2. – P. 172–186.
36. Walcott S., Sun S. X. Hysteresis in cross-bridge models of muscle // Phys. Chem. Chem. Phys. – 2009.– No 24. – P. 4871–4881.
37. Wu J. Z., Herzog W., Cole G. K. Modeling dynamic contraction of muscle using the cross-bridge theory // Math. Biosci. – 1997.– No 1. – P. 69–78.
38. Zahalak G. I. A distribution-moment approximation for kinetic theories of muscular contraction // Math. Biosci. – 1981.– No 1-2. – P. 89–114.