АНАЛИЗ ДИАГРАММ РАССЕЯНИЯ НЕЛИНЕЙНО ВЗАИМОДЕЙСТВУЮЩИХ АКУСТИЧЕСКИХ ВОЛН НА ВЫТЯНУТОМ СФЕРОИДЕ
Аббасов И.Б.1, Заграй Н.П.2
1Доцент, доктор технических наук, 2профессор, доктор технических наук, Инженерно-технологическая академия Южного федерального университета
АНАЛИЗ ДИАГРАММ РАССЕЯНИЯ НЕЛИНЕЙНО ВЗАИМОДЕЙСТВУЮЩИХ АКУСТИЧЕСКИХ ВОЛН НА ВЫТЯНУТОМ СФЕРОИДЕ
Аннотация
В работе проведен анализ и сравнение диаграмм рассеяния акустических волн на вытянутом жестком сфероиде. Представлены расчетные диаграммы рассеяния плоской акустической волны на вытянутом сфероиде и вытянутых металлических сфероидальных оболочках. Для сравнения использованы построенные диаграммы рассеяния акустического давления волны разностной частоты.
Ключевые слова: диаграммы рассеяния, вытянутый сфероид, волна разностной частоты.
Abbasov I.B.1, Zagrai N.P.2
1Associate professor, Doctor of Engineering, 2professor, Doctor of Engineering, Engineering Technological Academy of Southern Federal University
ANALYSIS THE SCATTERING DIAGRAMS OF NONLINEARLY INTERACTING ACOUSTIC WAVES BY AN ELONGATED SPHEROID
Abstract
The article is dedicated analyzes and comparison the scattering diagrams of acoustic waves by elongated hard spheroid. Are presented the calculated scattering diagrams the plane acoustic wave by an elongated spheroid and elongated metallic spheroidal shells. For comparison used computed scattering diagrams of acoustic pressure of the difference frequency wave.
Keywords: scattering diagrams, elongated spheroid, difference frequency wave.
При освоении водных акваторий часто применяются гидроакустические системы с использованием параметрических излучающих антенн на основе нелинейных эффектов. Водная среда играет важную роль в формировании полей акустических параметрических антенн, необходимо учитывать различия между идеальными и реальными условиями работы. В реальных условиях работы морская среда всегда имеет неоднородности различного происхождения. К ним относятся, как локальные неоднородности самой среды, так и неоднородности биологического и искусственного характера.
Аналитические решения задач рассеяния возможны только для тел простой формы – сфер, цилиндров, сфероидов, дисков, частей плоскостей, а для произвольного тела обычно задача рассеяния решается с помощью численных методов математического моделирования. Задача рассеяния нелинейно взаимодействующих плоских акустических волн на жестком вытянутом сфероиде была исследована в работах [1, 2].
Сфероид образуется вращением эллипса вокруг большой оси. Фокусы сфероида совпадают с фокусами сфероидальной системы координат. Нелинейные волновые процессы, происходящие между падающими и рассеянными волнами, описываются неоднородным волновым уравнением. Данное уравнение методом последовательных приближений разложения в ряд по малому параметру. В первом приближении решение однородного волнового уравнения характеризует падающие и рассеянные исходные волны накачки. Решения во втором приближении для акустического давления волн вторичного поля, представляют объемный интеграл, состоящий из произведения функции вторичных источников и функции Грина. Объем интегрирования представляет собой сфероидальный слой среды вокруг рассеивателя.
Решение во втором приближении состоит из четырех частотных составляющих: вторых гармоник падающих волн и волн комбинационных частот. Были получены асимптотические выражения для акустического давления волны разностной частоты и построены диаграммы рассеяния [3]. В данной работе представлен анализ диаграмм рассеяния акустических волн на вытянутом сфероиде.
Следует отметить, что в нелинейной постановке данная задача теоретически и экспериментально ранее не исследовалась. В рамках нашего рассмотрения для первичных высокочастотных волн рассеяние на сфероиде является линейным. Вторичное поле создается этими рассеянными полями. Поэтому рассмотрим некоторые результаты по линейному рассеянию на вытянутом сфероиде и сфероидальных оболочках.
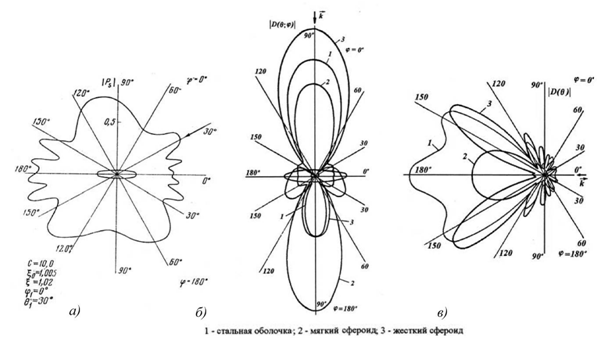
В работах часто приведены диаграммы рассеяния при углах падения акустических волн θ=0° и 90° [4, 5]. На рис.1 представлены расчетные диаграммы рассеяния плоской акустической волны на вытянутом сфероиде при различных углах падения [6].
Рис.1 - Диаграммы рассеяния на вытянутом сфероиде: а) мягкий сфероид kh=10, ξ0=1,005, θ=30°; б) жесткий сфероид (3) kh=5, ξ0=1,005, θ=90°; в) жесткий сфероид (3) kh=10, ξ0=1,005, θ=0°.
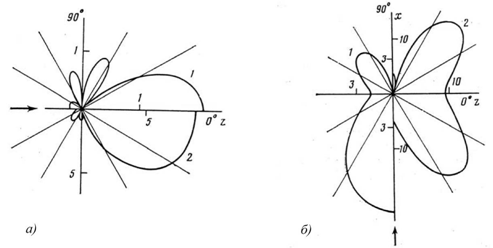
Рассмотрим ещё одни диаграммы рассеяния, на рис.2 представлены диаграммы рассеяния плоской волны на вытянутых металлических сфероидальных оболочках (при δ=1 оболочки превращаются в упругий сфероид) [7].
Рис.2 - Диаграммы рассеяния на вытянутых сфероидальных оболочках: а) стальная, kh=1,47, θ=0°, δ=0,2 (1), 0,05 (2); б) медная (1) kh=2,02, латунная (2) kh=2,12, θ=90°, δ=0,2.
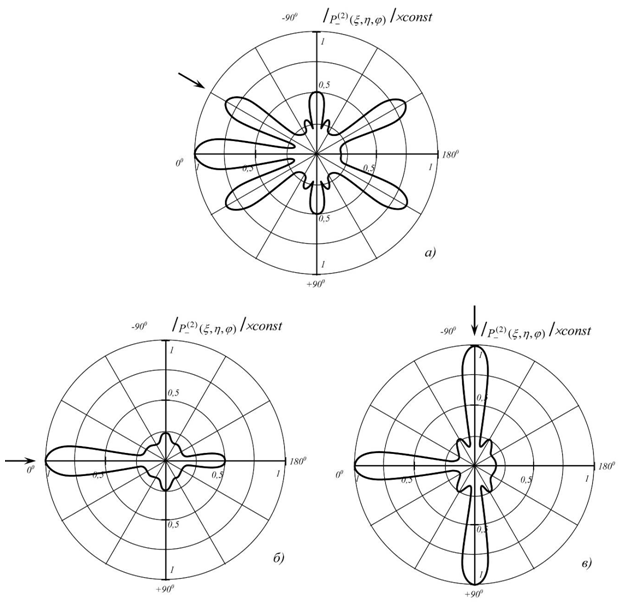
Для сравнения на рис.3 представлены рассчитанные на основе асимптотических выражений диаграммы рассеяния волны разностной частоты на вытянутом сфероиде при разных углах падения плоских волн.
Из сравнения диаграмм рассеяния представленных на рис.1 и 3 отметим следующее:
- диаграмма рассеяния на рис.1 имеет максимумы симметричные углу падения θ=30°(отраженные лепестки), при угле падения θ=0° преобладает рассеяние в направлении распространения, при угле падения θ=90°(боковое падение) существуют только два максимума в прямом и обратном направлениях, превалирующим является обратное рассеяние;
- диаграмма рассеяния на рис.3 при угле падения θ=30° имеет также максимумы симметричные углу падения, при угле θ=0° преобладает рассеяние в обратном направлении, при угле θ=90° имеются также максимумы в направлении распространения, и в обратном направлении, но наблюдается ещё в максимум в перпендикулярном направлении.
Рис.3 - Диаграммы рассеяния волны разностной частоты Pˍ(2)(ξ,η,φ) на жестком вытянутом сфероиде ξ0=1,005 при: f2=1000 кГц, ξ=7; а)f1=880 кГц, Fˍ=120 кГц, kˍh0=5, θ=30°; б)f1=976 кГц, Fˍ=24 кГц, kˍh0=1, θ=0°; в) θ=90°.
Проведем сравнение диаграмм рассеяния представленных на рис.2 с построенными диаграммами на рис.3:
- диаграмма рассеяния на рис.3 при угле падения θ=0° имеет превалирующий максимум в теневой области, а также наблюдаются боковые лепестки, на диаграмме (рис.3б) имеются аналогичные максимумы по направлениям, хотя разные по уровню;
- при угле падения θ=90° имеются максимумы в обратном направлении и по направлению распространения (для медной оболочки), диаграмма в нашем случае (рис.3в) кроме этих максимумов, ещё имеет максимум в перпендикулярном направлении.
Надо отметить, что в нашем случае рассеянное поле создается источниками вторичных волн расположенных в объеме вокруг сфероида. В линейном случае они располагаются на поверхности самого сфероида. В целом можно подчеркнуть, что построенные диаграммы рассеяния находятся в хорошем согласии с приведенными диаграммами [6,7].
Учитывая, что в дальнем поле сфероидальные координаты переходят в сферические (h0→0) и Pˍ(2)(ξ,η,φ)→Pˍ(2)(r,θ,φ) для сравнения распределений акустического давления вдали от рассеивателя можно использовать результаты, представленные в работе [2] по рассеянию на сфере. Диаграммы рассеяния на вытянутом сфероиде достаточно хорошо согласуются в дальнем поле с результатами исследований по рассеянию на сфере. Однако в отличие от сферы, где рассеянное поле не зависит от угла падения θ, для сфероида появляются лепестки по направлениям падения и отражения исходных плоских волн.
Литература
- Аббасов И.Б. Рассеяние поля акустической параметрической антенны на объектах сфероидальной формы //Доклады Академии наук. – 2006. –Т.410. –№1. С.42-44.
- Аббасов И.Б. Рассеяние нелинейно-взаимодействующих акустических волн: сфера, цилиндр, сфероид. М.: Физматлит, 2007. 160с.
- Abbasov I.B. Study of the scattering of nonlinearly interacting plane acoustic waves by an elongated spheroid //Journal of Sound and Vibration. – 2008. – V.309. –№1-2. P.52-62. http://dx.doi.org/10.1016/j.jsv.2007.03.060
- Клещев А.А., Шейба Л.С. Рассеяние звуковой волны идеальными вытянутыми сфероидами //Акуст. журн. –1970. –Т.16. –№2. С.264-268.
- Федорюк М.В. Рассеяние звуковых волн тонким акустически жестким телом вращения //Акуст. журн. –1981. –Т.27. –№4. С.605-609.
- Клещев А.А. Дифракция, излучение и распространение упругих волн. С.-Пб.: Изд. ООО «Архей», 160с.
- Бойко А.И., Максимова Н.О. Дифракция плоской звуковой волны на оболочке вращения //Акуст. журн. –1988. –Т.34. –№1. С.40-42.
References
- Abbasov I.B. Scattering of the parametric-antenna acoustic field by spheroidal objects //Doklady Physics. – 2006. –V.51. –№ 9. P.490 – 492.
- Abbasov I.B. Scattering of nonlinear interacting acoustic waves: sphere,cylinder and a spheroid: M: Fizmatlit, 2007. 160p.
- Abbasov I.B. Study of the scattering of nonlinearly interacting plane acoustic waves by an elongated spheroid //Journal of Sound and Vibration. –2008. –V.309. –№1-2. 52-62. http://dx.doi.org/10.1016/j.jsv.2007.03.060
- Kleshchev A.A., Sheyba L.S. Rasseyaniye zvukovoy volny ideal'nymi vytyanutymi sferoidami //Akust. zhurn. – –T.16. –№2. S.264-268.
- Fedoryuk M.V. Rasseyaniye zvukovykh voln tonkim akusticheski zhestkim telom vrashcheniya //Akust. zhurn. – –T.27. – №4. S.605-609.
- Kleshchev A.A. Difraktsiya, izlucheniye i rasprostraneniye uprugikh voln. S.-Pb.: Izd. OOO «Arkhey», 2006. 160s.
- Boyko A.I., Maksimova N.O. Difraktsiya ploskoy zvukovoy volny na obolochke vrashcheniya //Akust. zhurn. – –T.34. – №1. S.40-42.