Термодиффузия в разреженных трехкомпонентных газовых системах, содержащих N2, Ne, Ar и CO2
Термодиффузия в разреженных трехкомпонентных газовых системах, содержащих N2, Ne, Ar и CO2
Аннотация
Работа посвящена экспериментальному и теоретическому исследованию термодиффузии в трехкомпонентных газовых системах N2 – Ar – CO2 и Ne – Ar – CO2. Измерения проведены с помощью модифицированного двухколбового аппарата при температурах холодной и горячей области газовой смеси T1 = 280 К, T2 = 800 К, соответственно, давлении P = 0,1 МПа и различных составах смеси. Полученные величины разделения и термодиффузионные постоянные сопоставлены с расчетами по ранее предложенной формуле, позволяющей определять значения термодиффузионных характеристик трехкомпонентных систем через параметры бинарных смесей газов. Сравнение показывает неплохое согласие между экспериментом и расчетом в исследованном диапазоне термодинамических параметров.
1. Введение
Во многих технологических процессах в качестве рабочего тела выступают смеси газов, находящиеся при давлениях, близких к атмосферному. Поэтому при их рассмотрении требуется учет явлений переноса массы и тепла таких как диффузия и термодиффузия , , . Сущность явления термодиффузии состоит в том, что при наложении градиента температуры на первоначально однородную газовую смесь происходит частичное разделение ее на компоненты. При этом легким газом обогащается область с более высокой температурой, более тяжелым газом – холодная область.
Анализ научных публикаций, посвященных вопросам термодиффузии в газах, показывает наличие достаточно обширных исследований данного явления в бинарных смесях газов , , , . Особый интерес представляют смеси трех и более газов в силу того, что для них отсутствует строгая теория, позволяющая с высокой точностью рассчитать их термодиффузионные характеристики. Это связано с тем, что если для бинарных систем удается найти согласие между теорией и экспериментом , , , то для многокомпонентных такое согласие наблюдается лишь для отдельных смесей , , , . При вычислениях по строгой кинетической теории отклонение расчета от эксперимента достигает 50%, по элементарной – 100% , , , .
В силу сложности экспериментальных исследований число работ, посвященных термодиффузии в многокомпонентных газовых системах, невелико. В этой связи расширение объема экспериментальных данных по термодиффузии в разреженных трехкомпонентных газовых системах, в том числе, ранее не исследованных, является актуальной задачей.
2. Методы и принципы исследования
В данной работе проведен эксперимент по определению термодиффузионных характеристик газовых смесей с помощью модифицированного двухколбового аппарата , . Это трубка с изотермическими областями на ее концах с присоединенными к ним замкнутыми контурами, по которым циркулирует газовая смесь. Для обеспечения циркуляции газа по контурам в схему включен термогравитационный насос. Собственно колбами аппарата являются изотермические области и замкнутые контуры. Анализ смеси до и после разделения проводился совместно двумя методами: весовым и интерферометрическим, что позволяло определить состав смеси и рассчитать разделение всех трех компонентов. В работе использовался интерферометр типа Рэлея – ИТР-1 со специально изготовленной металлической кюветой длиной 1,2 м. Взвешивание баллончиков с газовой смесью осуществлялось на весах фирмы Меттлер, давление в установке контролировалось манометром бюро поверок.
В работах , , , нами был приведен и апробирован для ряда газовых систем метод расчета термодиффузионного разделения, Δxi, в многокомпонентных системах, основанный на соотношении, полученном Вальдманом . Формула имеет вид:
где Δxij – величина термодиффузионного разделения i-го компонента в бинарной газовой смеси, определяемая соотношением:
где xi, xj – объемная доля i-го и j-го компонента в трехкомпонентной газовой смеси; xij, xjj – объемные доли i-го и j-го компонента в соответствующей бинарной смеси газов; mi, mj – масса молекул сорта i и j, кг; aij =Aijxij + Bij – эмпирический коэффициент .
Соотношение (1) действительно если температура, при которой вычисляется Δxi, равна температуре холодной и горячей областей при нахождении Δxij. Вторым условием является равенство отношений концентраций i-го и j-го компонентов в бинарной и многокомпонентной смесях
Используя полученные в ходе эксперимента значения термодиффузионного разделения многокомпонентной смеси Δxi, определим термодиффузионные постоянные по следующей формуле , , :
Величины Δxi и Δxj в формуле (3) имеют знак плюс, если данным компонентом обогащается горячая область, и минус, если холодная.
Теоретическое определение термодиффузионной постоянной трехкомпонентных газовых систем возможно при использовании формулы, предложенной и апробированной нами в работах , :
Термодиффузионные постоянные бинарных смесей газов можно вычислить или получить экспериментально. При этом необходимыми условиями при нахождении термодиффузионных постоянных бинарных смесей, участвующих в формуле (4), являются равенство температур горячей и холодной областей в трехкомпонентной и бинарных смесях, а также отсутствие тройных столкновений молекул. В данной работе мы рассчитывали значения по формуле (2) с учетом безразмерных эмпирических коэффициентов Aij и Bij (см. табл. 1).
3. Основные результаты
В настоящей работе исследованы разреженные трехкомпонентные газовые системы N2 – Ar – CO2 и Ne – Ar – CO2. Проведен эксперимент по определению величин термодиффузионного разделения Δxi (см. рис. 1, табл. 2) и термодиффузионной постоянной (см. рис. 2 – 4) в зависимости от изменения содержания одного из компонентов x(доб). Измерения проводились при давлении P = 0,1 МПа, температурах холодной и горячей областей газовой смеси Т1 = 280 К, Т2 = 800 К соответственно.
Таблица 1 - Эмпирические коэффициенты Aij и Bij для бинарных систем, включающих N2, Ne, Ar, и CO2
Газовая система | Aij | Bij |
Ar-CO2 | 0,29±0,11 | 1,09±0,06 |
Ne-Ar | –0,25±0,11 | 1,11±0,05 |
Ne-CO2 | –0,44±0,06 | 1,05±0,05 |
N2-Ar | 0,57±0,09 | 0,81±0,05 |
N2-CO2 | –0,030±0,004 | 1,471±0,025 |
Таблица 2 - Экспериментальные и расчетные значения термодиффузионного разделения в системе N2 – Ar – CO2
x (доб) | Эксперимент | Расчет | Отклонение эксперимента от расчета, % | ||||||
Δx(N2) | Δx(Ar) | Δx(CO2) | Δx(N2) | Δx(Ar) | Δx(CO2) | ε1 | ε2 | ε3 | |
x(N2)/x(CO2)=1,005, T1 = 280 K, T2 = 800 K | |||||||||
0,105 | 0,0164 | -0,0025 | -0,014 | 0,0162 | -0,0024 | -0,0139 | 1,22 | 4,00 | 0,71 |
0,310 | 0,0162 | -0,0069 | -0,0093 | 0,0165 | -0,0068 | -0,0097 | 1,85 | 1,45 | 4,30 |
0,507 | 0,0149 | -0,0088 | -0,0061 | 0,0152 | -0,0090 | -0,0062 | 2,01 | 2,27 | 1,64 |
0,708 | 0,0116 | -0,0084 | -0,0032 | 0,0113 | -0,0082 | -0,0032 | 2,59 | 2,38 | 0,00 |
0,908 | 0,0045 | -0,0036 | -0,0009 | 0,0043 | -0,0035 | -0,0008 | 4,44 | 2,78 | 11,11 |
x(Ar)/x(CO2)=1,006, T1 = 300 K, T2 = 900 K | |||||||||
0,112 | 0,0082 | -0,0010 | -0,0072 | 0,0080 | -0,0009 | -0,0071 | 2,44 | 10,00 | 1,39 |
0,298 | 0,0161 | -0,0071 | -0,0090 | 0,0163 | -0,0069 | -0,0094 | 1,24 | 2,82 | 4,44 |
0,497 | 0,0186 | -0,0089 | -0,0097 | 0,0190 | -0,0089 | -0,0101 | 2,15 | 0,00 | 4,12 |
0,712 | 0,0156 | -0,0075 | -0,0081 | 0,0152 | -0,0072 | -0,0080 | 2,56 | 4,00 | 1,23 |
0,895 | 0,0069 | -0,0031 | -0,0038 | 0,0068 | -0,0032 | -0,0036 | 1,45 | 3,23 | 5,26 |
Среднее отклонение эксперимента от расчета, % | 2,28 | 3,30 | 3,22 | ||||||
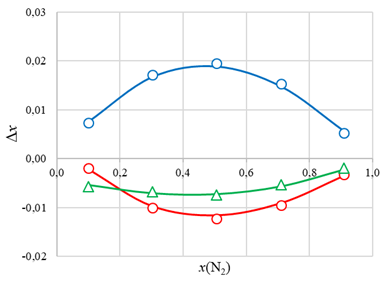
Рисунок 1 - Зависимость термодиффузионного разделения Δx системы N2 – Ar – CO2 при x(Ar)/x(CO2)=1,755 от x(N2) при температурах T1 = 280 К, T2 = 800 К:
○, □, ∆ – экспериментальные значения Δx для N2, Ar и CO2;
—— – расчет по формуле (1)
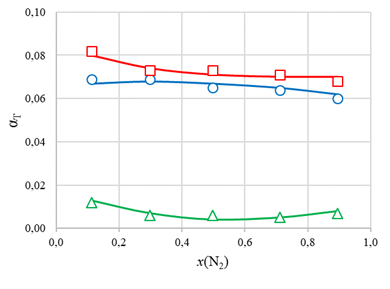
Рисунок 2 - Зависимость термодиффузионных постоянных αijT системы N2 – Ar – CO2 при x(Ar)/x(CO2)=1,006 от x(N2), при T1 = 280 К и T2 = 800 К:
○, □, ∆ – эксперимент для αT(N2-Ar), αT(N2-CO2), αT(Ar-CO2);
—— – расчет по формуле (3)
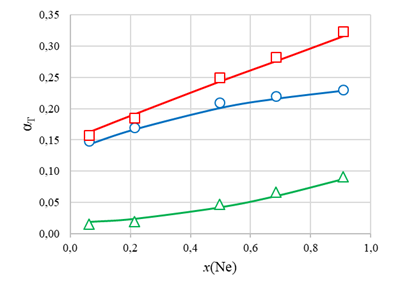
Рисунок 3 - Зависимость термодиффузионных постоянных αijT системы Ne – Ar – CO2 при x(Ar)/x(CO2)=0,998 от x(Ne) при T1 = 280 К и T2 = 800 К:
○, □, ∆ – эксперимент для αT(Ne-Ar), αT(Ne-CO2), αT(Ar-CO2);
—— – расчет по формуле (3)
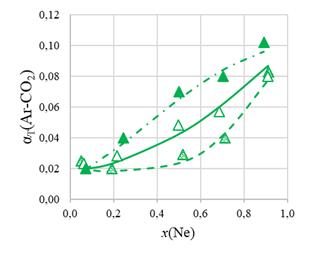
Рисунок 4 - Зависимость величины термодиффузионной постоянной αT(Ar-CO2) от содержания третьего компонента при T1 = 280 К, T2 = 800 К в газовой системе Ne – Ar – CO2 от мольной доли x(Ne):
○, □, ∆ – эксперимент для αT(Ar-CO2) при x(Ar)/x(CO2) = 0,252; 0,998 и 4,007;
—— – расчет по формуле (3)
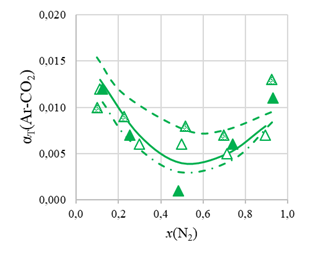
Рисунок 5 - Зависимость величины термодиффузионной постоянной αT(Ar-CO2) от содержания третьего компонента при T1 = 280 К, T2 = 800 К в газовой системе N2 – Ar – CO2 от мольной доли x(N2):
○, □, ∆ – эксперимент для αT(Ar-CO2) при x(Ar)/x(CO2) = 0,252; 0,998 и 4,007; —— – расчет по формуле (3)
Для экспериментальных значений термодиффузионных постоянных также было проведено сопоставление с расчетами по полуэмпирической формуле (4), показавшее неплохое согласие между ними (см. рис. 2–5). Исключение составляют значения αT(Ar-CO2) в системе Ne-Ar-CO2 (см. рис. 5). Больший разброс в данном случае связан с малыми значениями термодиффузионной постоянной.
4. Заключение
Главным результатом данной работы является получение термодиффузионных характеристик для ранее не исследованной газовой системы Ne – Ar – CO2, а также расширение объема экспериментальных данных по термодиффузии в системе N2 – Ar – CO2. Проанализировав полученные данные можно сделать вывод о сложном характере зависимости термодиффузионных характеристик от состава исследованных трехкомпонентных газовых смесей.
Экспериментальные значения термодиффузионных постоянных, полученные в рамках исследования, сравнены с рассчитанными по предложенной нами ранее полуэмпирической формуле. Между результатами эксперимента и значениями, рассчитанными по приведенным методикам, наблюдается неплохое согласие, среднее отклонение составляет около 3%. Это позволяет рекомендовать указанную формулу для расчета термодиффузионных характеристик в трехкомпонентных газовых системах, содержащих N2, Ne, Ar и CO2 при давлениях, близких к атмосферному.