Проектирование оптимальной структуры виртуальной организации с помощью алгоритмов кластеризации

Иерархия целей организации определяется выбранными стратегическими целевыми установками, и реализуется методами, предусмотренными в миссии организации с учетом условий внешней среды

Многие исследователи сходятся в том, что сетевая модель взаимодействия субъектов экономики является одной из наиболее эффективных с точки зрения инновационного развития

С одной стороны, создание отдельного подразделения для решения каждой элементарной задачи экономически нецелесообразно. С другой – наличие у подразделения большого количества не связанных между собой обязанностей обычно приводит к невозможности построить цельную пирамиду средне- и долгосрочных целей на уровне подразделений, и как следствие – к непониманию персоналом глобальной цели своих действий и снижению эффективности работы подразделения в целом. Поэтому эффективное распределение обязанностей между подразделениями позволяет оптимизировать структуру предприятия и повысить производительность как отдельных подразделений, так и организации в целом.

Таким образом, возникает необходимость оптимального распределения обязанностей, при котором минимизируется внешняя сцепленность и максимизируется внутренняя связность кластера задач, выполняемых каждым подразделением.

Рассмотрим виртуальную организацию на этапе становления ее структуры. Допустим, в результате декомпозиции основных целей, с учетом миссии фирмы и условий внешней среды было выделено множество элементарных задач x, решение которых и составляет процесс функционирования предприятия.

Каждая элементарная задача может быть представлена в виде объекта x = {a1, a2,… am}, элементы которого ak – это параметры, характеризующие ключевые показатели задачи, такие как трудоемкость, предметная область, требования к исполнителям и т.д. Отметим, что число таких характеристик должно определяется индивидуально для каждой системы задач.

Проблема выделения ключевых параметров ak является довольно сложной и плохо формализуемой задачей. Наиболее эффективный способ ее решения, на наш взгляд, – использование экспертной оценки с целью определения наиболее значимых факторов, характеризующих процессы, лежащих в основе решения задачи. Мы выделили следующие категории характеристик, которые могут служить для описания процесса решения бизнес-задач:

– необходимые ресурсы (материальные, финансовые, интеллектуальные);

– методы и способы решения задачи;

– технологические средства решения задачи;

– область знаний, к которым относится задача;

– территориальное расположение места выполнения задачи;

– личностные особенности сотрудника, необходимые для решения задачи (методичность, коммуникативность, креативность) и т.д.

Введем основные показатели для оценки эффективности функционирования подразделений предприятия. Величина производственных издержек подразделения G(n, x1, x2… xn) является функцией числа n возложенных на подразделение задач и тех параметров ak, которые характеризуют ресурсы, необходимые для решения этих задач. При удачном сочетании обязанностей в подразделении наблюдается эффект синергии, выражаемый формулой

(1)

То есть одно крупное подразделение имеет меньшие издержки производства, чем несколько мелких подразделений, выполняющих те же задачи.

Доходность подразделения D(n, k1, k2, … kn) также определяется числом n выполняемых задач и показателями ki прибыльности задач.

Эффективность j-го подразделения можно определить следующим образом:

(2)

где – величина дисперсии задач подразделения.

Множитель H учитывает отрицательный эффект, который возникает в случае, когда на подразделение возлагается много разнородных задач. Этот эффект тем больше, чем дальше расположены друг от друга задачи подразделения в пространстве переменных ak. Эффективность организации в целом определяется как сумма

(3)

Таким образом, проблема проектирования наиболее эффективной структуры организации в предложенной модели сводится к максимизации функционала F.

Сложность решения поставленной задачи заключается в определении аналитического вида функций Dj, Gj и Hj. Если для описания функций доходности и издержек существуют различные экономические модели, то построить аналитическую модель эффекта «распыления», который описывает функция Н, вряд ли возможно. Кроме того, задача осложняется тем, что переменными являются не только значения элементов ak объектов x, но и число n этих объектов.

Отметим, что из предложенного выше вида функции H следует, что она принимает наименьшее значение в том случае, когда задачи функционального подразделения максимально близки друг к другу в пространстве переменных ak. Следовательно, для нахождения наиболее выгодных для подразделения комбинаций, необходимо разделить множество элементарных задач x на компактные группы в соответствии с их характеристиками. Эта задача известна как задача кластеризации и методы ее решения достаточно хорошо изучены. В общем виде кластеризацию можно описать как объединение объектов в группы на основании их сходства по ряду признаков. На сегодняшний день известно несколько десятков алгоритмов кластеризации, работающих с разными типами характеристик объектов и по-разному трактующими понятие сходства.

Все атрибуты объектов можно разделить на числовые и категориальные

Большинство алгоритмов кластеризации числовых атрибутов основаны на оптимизации некоторой функции, определяющей степень близости объектов, входящих в кластер. Часто в качестве такой функции выступает расстояние от центра кластера до входящих в него объектов.

В рамках решения задачи оптимизации структуры используются одновременно и числовые, и категориальные характеристики задач. Например, возможны следующие конфигурации объектов, описывающих организацию со свойствами «сфера деятельности», «размер бизнеса» и «количество сотрудников»:

х1 = {торговля, средний, 120};

х2 = {образование, малый, 25}.

Если для оценки расстояния между этими объектами используется иерархический алгоритм с мерой сходства, нам необходимо привести значения атрибута «Количество сотрудников», измеренные по шкале отношений к порядковой шкале (т.е. дискредитировать атрибут). Например, так:

х1 = {торговля, средний, больше 100};

х2 = {образование, малый, меньше 100}.

Такая операция допустима, поскольку порядковая шкала слабее шкалы отношений, но при дискредитации всегда утрачивается часть информации об объекте. В данном случае мы потеряем сведения о точном числе сотрудников.

Если же использовать в качестве метрики евклидово расстояние, то возникают проблемы с категориальными атрибутами, поскольку перевод значений из слабой шкалы в более мощную недопустим. Дополнительную сложность создает потенциально различная степень важности атрибутов при принятии решения о группировке задач.

Наиболее перспективными механизмами кластеризации объектов со смешанными атрибутами нам представляются масштабируемые алгоритмы, оптимизирующие не локальные функции расстояния до центра кластера, а глобальную функцию. К этому типу относятся алгоритмы CLOPE

Например, нужно кластеризовать следующее множество объектов: x1={a, b}, x2={a, b, c}, x3={a, c, d}, x4={d, e}, x5={d, e, f}. Сравним два варианта разбиения:

1) {x1, x2, x3}; {x4, x5} и 2) {x1, x2}; {x3, x4, x5}.

Для первого и второго вариантов разбиения в каждом кластере рассчитаем количество вхождений в него каждого элемента и представим эти разбиения виде гистограмм

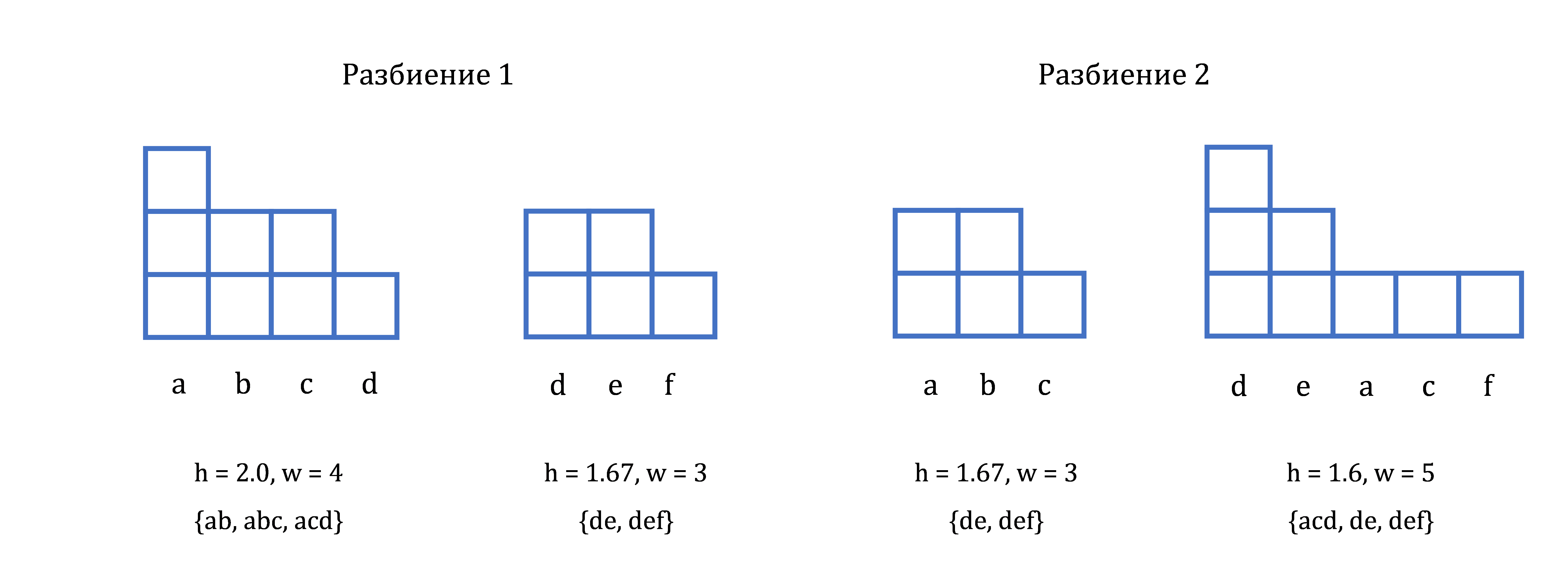
Рисунок 1 - Гистограммы разбиений исходного множества объектов

DOI:10.23670/IRJ.2023.132.123.1

Количество разных параметров, входящих в кластер, назовем шириной гистограммы w, общее количество параметров для всех задач кластера назовем площадью гистограммы s, тогда высота гистограммы h будет рассчитываться как отношение s к w. Степень близости задач, входящих в кластер, определяется значением параметра h для кластера. Чем выше этот параметр, тем больше наложение задач друг на друга. Функцией, служащей основой оптимизации разбиений может служить суммарная высота всех кластеров. В приведенном примере разбиение (1) лучше, поскольку обеспечивает большее совпадение задач и соответственно, параметр h там выше (h1 = 3,67; h2 = 3,27).

В том случае, если разные разбиения дают одинаковое значение h можно использовать дополнительный параметр сравнения – градиент g = h/w = s/w2. Чем выше показатель g(q), тем лучше разбиение q. Глобальная функция сходства p(q) может быть рассчитана по формуле:

(4)

где r – параметр отталкивания, который регулирует степень сходства объектов внутри кластера, r>1.

Итак, рассмотренный алгоритм дает возможность выделить кластеры схожих задач, после чего можно оптимизировать структуру организации путем определения отдельного функционального подразделения для решения каждой выделенной группы задач. Степень сходства задач в кластере можно регулировать изменяя параметр r : чем выше значение r, тем мельче будут кластеры и тем больше кластеров будет выделено.

Таким образом, задача формирования оптимальной структуры виртуального предприятия была сведена нами к задаче выделения кластеров на множестве элементарным задач, решение которых необходимо для функционирования организации. Выбор атрибутов, характеризующих эти задачи, зависит от специфики деятельности организации, однако можно выделить ряд общих параметров, таких как необходимые ресурсы, методы и способы решения задачи, территориальное расположение и др. Поскольку большинство перечисленных параметров являются категориальными, для кластеризации предлагается использовать масштабируемые алгоритмы, наиболее эффективным из которых можно считать алгоритм CLOPE.

Отметим, что предложенный способ оптимизации структуры подходит для виртуальной организации любой отрасли. Конкретный вид структуры зависит от того, с какой степенью детализации будет выполнен анализ целей и задач на начальном этапе, а также от того по какому признаку будут сгруппированы полученные элементарные задачи. Так, если в качестве наиболее весомого параметра кластеризации выбрана принадлежность задачи к определенному бизнес-процессу, то выделенные подразделения могут рассматриваться как процессные команды и т.д.