ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ТЕМПЕРАТУРНОГО РЕЖИМА МЕРЗЛЫХ ГРУНТОВ ОСНОВАНИЯ ВЗЛЕТНО-ПОСАДОЧНОЙ ПОЛОСЫ Г. ЯКУТСКА

ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ТЕМПЕРАТУРНОГО РЕЖИМА МЕРЗЛЫХ ГРУНТОВ ОСНОВАНИЯ ВЗЛЕТНО-ПОСАДОЧНОЙ ПОЛОСЫ Г. ЯКУТСКА

Научная статья

Слепцов А.А.^1, *, Рожин И.И.²

¹ ORCID: 0000-0002-0782-9810;

² ORCID: 0000-0002-9998-6425;

¹ Северо-Восточный федеральный университет им. М.К. Аммосова, Якутск, Россия;

² Якутский научный центр СО РАН Институт проблем нефти и газа СО РАН, Якутск, Россия

* Корреспондирующий автор (msleptsova[at]mail.ru)

Аннотация

Рассматривается проект реконструкции второй взлетно-посадочной полосы (ВПП) длиной в 3400 м аэропорта на территории г. Якутска Республики Саха (Якутия). В данной работе исследуется температурный режим основания взлетно-посадочной полосы аэропорта. Математическая модель постановки задачи динамики температурного поля в массиве выполнена на основе общей постановки задач типа Стефана. Здесь рассчитаны температурные поля массива грунтов под насыпью ВПП в различные моменты времени (от 1 года до 100 лет) в следующем варианте: армобетон (0,24 м), цементобетон (0,24 м), насыпной грунт (0,68 м) и пеностирол (0,08 м). Также рассчитаны глубины оттаивания основания ВПП. Укладка теплоизоляции в основание ВПП позволяет значительно увеличить его теплоустойчивость.

Ключевые слова: взлетно-посадочная полоса, теплоизоляция, задача Стефана, математическое моделирование.

A NUMERICAL STUDY OF THE TEMPERATURE REGIME OF FROZEN BOTTOM SOILS OF THE RUNWAY IN YAKUTSK

Research article

Sleptsov A.A.^1, *, Rozhin I.I.²

¹ ORCID: 0000-0002-0782-9810;

² ORCID: 0000-0002-9998-6425;

¹ Ammosov North-Eastern Federal University , Yakutsk, Russia;

² Yakut Research Center, Institute of Oil and Gas Problems of the Siberian Branch of the RAS, Yakutsk, Russia

* Corresponding author (msleptsova[at]mail.ru)

Abstract

The current article examines the project of reconstruction of the 3400 m second runway of the Yakutsk airport in the Republic of Sakha (Yakutia) and investigates the temperature regime of the airport runway subgrade. The mathematical model of setting the problem of the dynamics of the temperature field in the array is based on the general formulation of the Stefan-type problems. The study also calculates the temperature fields of the soil mass under the GDP embankment at various points in time (from 1 year to 100 years) in the following version: fiber-reinforced concrete(0.24 m), cement concrete (0.24 m), soil fill (0.68 m) and styrofoam (0.08 m). The depth of thawing of the second runway subgrade is also calculated. Laying thermal insulation in the base of the second runway subgrade allows for a significant increase in its heat resistance.

Keywords: runway, thermal insulation, Stefan-type problem, mathematical modeling.

Город Якутск расположен в зоне сплошной мерзлоты. Одним из стратегически важных объектов на территории города является аэропорт. Аэропорт расположен, где толщина слоя вечной мерзлоты достигает 300 метров. Исходя из этого был разработан уникальный проект реконструкции второй взлетно-посадочной полосы (ВПП) длиной в 3400 метров. Функционирование подобных объектов вызывает изменение всех компонентов природной среды, что приводит к изменению свойств оснований сооружений и сказывается на их устойчивости. На сегодняшний день повышение надежности транспортных сетей, построенных в зоне сплошной вечной мерзлоты, является актуальной задачей современной инженерной геокриологии и транспортной строительной отрасли.

Для проектирования ВПП нужно учитывать промерзание, морозное пучение и оттаивание влажного грунта, которые являются сложными термодинамическими процессами в промерзающих основаниях.

В данной работе методами математического моделирования исследуется температурный режим основания ВПП аэропорта на территории г. Якутска. Целью исследования является расчет глубины оттаивания грунтов под насыпью, состоящей из слоев данной последовательности: армобетон, цементобетон, насыпной грунт из песка со щебнем, гидроизоляционная пленка, пенополистирол. Рассматриваемая задача включает модель многослойной конструкции насыпи и основания, состоящей из различных слоев грунта.

При построении математической модели приняты следующие допущения.

1. Перенос тепла внутри массива грунта осуществляется только теплопроводностью, тем самым при расчете температурного поля пренебрегаем массообменными процессами. Это инженерное допущение принято вследствие наличия в насыпи полосы гидроизоляционной пленки.
2. Теплофизические характеристики слоев грунта считаются кусочно-постоянными для талого и мерзлого состояний, учитывая их малое изменение в рассматриваемом диапазоне температур.
3. Фазовое превращение влаги происходит при постоянной температуре фазового превращения 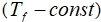, без изменения начальной влажности  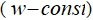и объема. В действительности же фазовое превращение «жидкость – твердое тело» отмечается при различных температурах и с некоторым изменением объема. Так, для водонасыщенного грунта фазовое превращение происходит и при температуре ниже 0^оС в зависимости от засоленности и влажности грунта, и с изменением влажности при его промерзании [1].

1. Математическая постановка задачи

Математическая постановка задачи динамики температурного поля в массиве выполнена на основе общей постановки задач типа Стефана. Модель включает квазилинейное уравнение теплопроводности с соответствующими краевыми условиями, которое с учетом многослойного массива имеет вид:

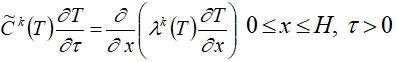    (1)

где  – коэффициент теплопроводности и объемная теплоемкость k-го слоя массива, которые аппроксимируются как кусочно-постоянные (сглаженные) функции по температуре T в окрестности фазового перехода. В данной работе используются следующие аппроксимации – линейная зависимость l(T) и параболическая  в окрестности фазового превращения:

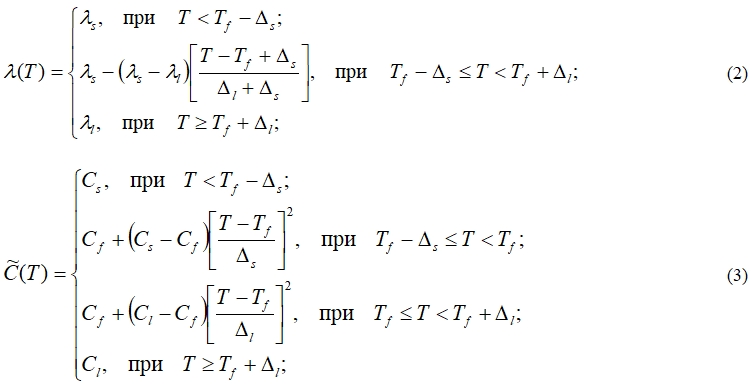
где Δ – температурные полуинтервалы сглаживания δ-функции Дирака, которые могут быть не равны друг другу (Δ_l ¹ Δ_s, Δ_l > 0, Δ_s > 0). Нижние индексы означают: f – фазовое превращение, l – жидкая фаза, s – твердая фаза. При этом скрытая теплота фазового превращения  фазового вводится с применением d-функции Дирака как сосредоточенная теплоемкость в коэффициент теплоемкости. Здесь l_f – удельная теплота фазового перехода «вода–лед», с_р – удельная теплоемкость воды, Т_f , r, w – температура фазового перехода, плотность и влажность k-го слоя массива соответственно.

Значение коэффициента теплопроводности при температуре фазового превращения:

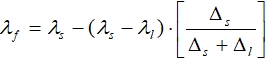
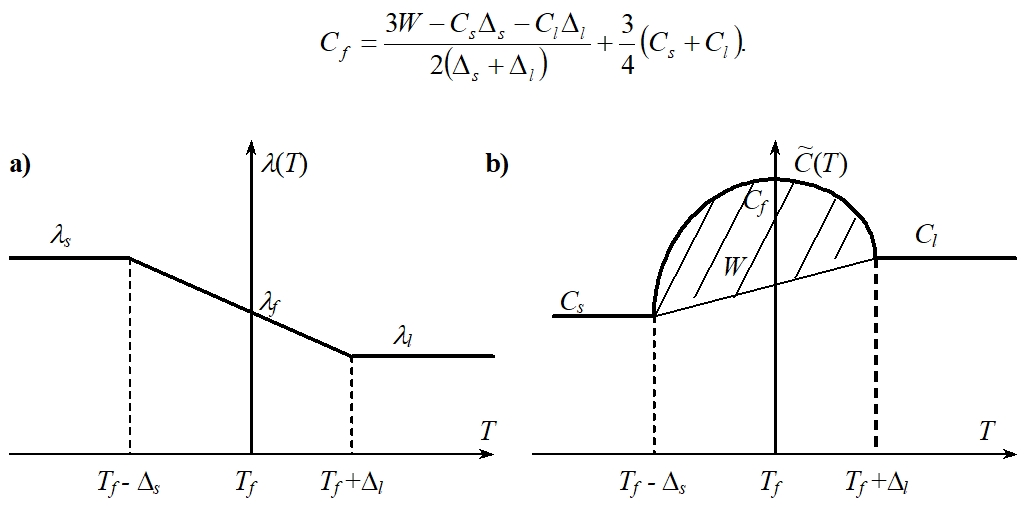
В выражении (3) неизвестную величину C_f определяем из равенства скрытой теплоты фазового превращения W количеству теплоты, получаемому при аппроксимации объемной теплоемкости в интервале температур от Т_f – Δ_s до Т_f + Δ_l и равному площади заштрихованной области (рис. 1), т.е.

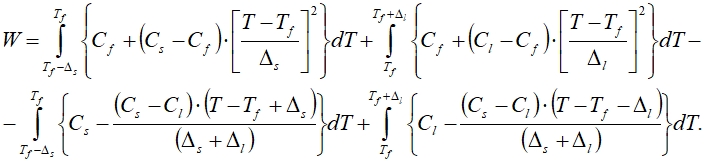Откуда после интегрирования определяется значение объемной теплоемкости при температуре фазового превращения:

Рис. 1 – Зависимость λ(Т) и  от температуры

 

Температурное поле в начальный момент времени (при ) задается в виде функции, зависящей только от координаты х:

    (4)

На границе между дневной поверхностью массива и окружающей средой принимается граничное условие III рода (закон Ньютона-Рихмана):

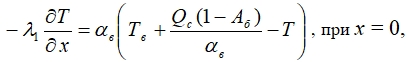   (5)

где λ₁ – коэффициент теплопроводности верхнего слоя массива (армобетона), Т_в – температура воздуха, Q_c – суммарная солнечная радиация, А_б – альбедо поверхности, a_в – коэффициент теплоотдачи от воздуха. Видно, что в уравнении (5) учитывается поступление тепла излучением [5].

На поверхностях, разделяющих слои массива, выполняются условия идеального теплового контакта, т.е. принимаются граничные условия IV рода: равенство температур и тепловых потоков непосредственно на границах между слоями.

Условием на нижней границе массива является условие тепловой изоляции на достаточно большом расстоянии теплового влияния:

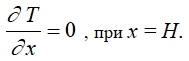    (6)

В разработанной математической модели основания взлетно-посадочной полосы учитываются изменения температуры воздуха со временем, воздействия суммарной солнечной радиации и альбедо поверхности, изменение коэффициента конвективного теплообмена в зависимости от скорости ветра.

Расчеты выполнены при исходных данных, включающих сведения о вещественном составе массива грунтов, их теплофизических характеристиках, данные термометрии. Недостающие данные были получены из опубликованной справочной или научной литературы.

В области многолетней мерзлоты эта задача существенно осложняется, так как здесь необходимо учитывать фазовый переход «лед – вода». Задачи такого рода называются задачами Стефана и для их численного решения используются методы, основанные на подходе, изложенном в монографии [2]. Для этого метода авторы работы [3] разработали экономичную разностную схему сквозного счета со сглаживанием разрывных коэффициентов в уравнении теплопроводности по температуре в окрестности фазового перехода. Схемы со сглаживанием коэффициентов предложены также в работе [4] и характеризуются тем, что граница раздела фаз явно не выделяется, что позволяет использовать однородные разностные схемы.

2. Численная реализация модели и алгоритм решения

Для применения разностного метода в области изменения переменных x, t вводятся пространственно-временные сетки – основную и потоковую

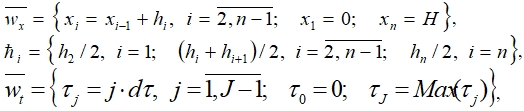
где h_i,  – шаги основной и потоковой пространственной сетки соответственно, n – количество узлов сетки по координате х; dτ – шаг временной сетки; J – максимальное число локальных итераций за время Мах(τ_j).

Тип сетки по координатам зависит от шага сетки. Так, например, для равномерной сетки шаг есть постоянная величина равная . При тех значениях аргумента, где функция резко меняется, шаг сетки должен быть малым, иначе точность вычисления по этой сетке будет плохой.

Сеточные методы основаны на замене дифференциальных уравнений эквивалентными алгебраическими соотношениями, которые содержат значения функции в отдельных дискретных точках – узлах сетки. Эти соотношения могут быть получены заменой производных, входящих в дифференциальное уравнение, их приближенными выражениями через разности значений функций в узлах сетки.

Исходное дифференциальное уравнение, таким образом, заменяется системой линейных алгебраических уравнений, начальные и граничные условия также заменяются разностными условиями для сеточной функции. В результате процесс решения сводится к выполнению несложных алгебраических операций. При формулировке разностных аппроксимаций обычно рассматриваются все пространственные узлы на нескольких прямых, соответствующих соседним значениям временной сетки (временным слоям). Процесс решения разностной задачи представляет определение значений искомой функции на всех временных слоях, исходя из известного начального ее распределения. С такой точки зрения разностная схема есть рекуррентное соотношение, связывающее соседние временные слои.

Как известно, явные разностные схемы почти всегда не пригодны для численного решения краевых задач параболического типа (1) из-за того, что они устойчивы лишь при неоправданно малых шагах временной сетки. Поэтому широкое распространение получили неявные разностные схемы.

Для получения консервативной разностной схемы, которая расписывается исходя из законов сохранения энергии в пределах ячейки (методом баланса или интегроинтерполяционным методом [6, 7]), интегрируется уравнение (1) по x ∈ [x_i-1/2, x_i+1/2]. В результате получим

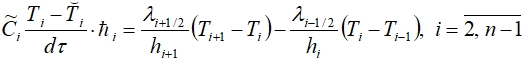     (7)

где верхний знак «∨» над T означает, что величина берется с нижнего временного слоя. При этом разностные аналоги теплофизических параметров (теплоемкости, коэффициента теплопроводности) вычисляются как некоторые средние значения теплофизических функций в пределах ячейки по выражениям (2) и (3):

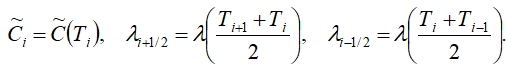
Распределение температуры Т_i определяется из системы линейных алгебраических уравнений (7) с соответствующими начальными и граничными условиями, которые имеют неособую трехдиагональную матрицу, что позволяет решать их методом прогонки. Пусть известно распределение температур на j-м временном слое и требуется определить распределение температур на (j+1)-м временном слое. Так как сглаженные коэффициенты зависят от температуры, получающаяся разностная задача будет нелинейной и решение разностного уравнения будет найдено методом простой итерации с использованием прогоночных алгоритмов. При этом процесс итерации повторяется до тех пор, пока не достигается наперед заданная точность.

Систему разностных уравнений (7) можно записать в каноническом виде:

    (8)

где приняты следующие обозначения: .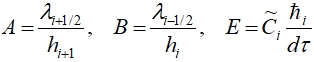

Решение системы уравнений (8) будем искать в виде

      (9)

где p_i, q_i – неизвестные коэффициенты, называемые прогоночными.

Соотношение (9) справедливо для всех значений индекса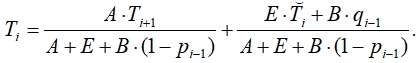 . Тогда подставляя значение  в (8), получим выражение Сравнивая последнее уравнение с (9) находим рекуррентные соотношения для определения прогоночных коэффициентов: 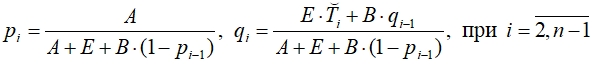    (10) Другие прогоночные коэффициенты определяются следующим образом. Из граничного условия (5) в точке при i = 1 имеем 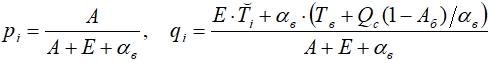     (11) При i = n с учетом условия тепловой изоляции (6) получим 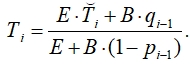    (12)

Решение задачи методом прогонки, разделяется на два этапа – сначала определяются прогоночные коэффициента p_i и q_i (прямая прогонка), затем вычисляются значения искомой функции (обратная прогонка). Число арифметических операций пропорционально числу уравнений.

Алгоритм численного решения одномерной задачи теплопроводности с фазовым переходом может описывается следующим образом:

1. Задаются геометрические и физические условия, а также начальное распределение температуры массива 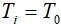 , дается нулевое приближение .
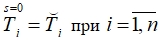2. Определяется температурное распределение в рассматриваемом массиве насыпи и ее основания при теплообмене с окружающей средой:

а) находятся прогоночные коэффициенты p_i и q_i для всех  по уравнениям (10), (11);

б) по известному значению Т_п (12), используя рекуррентную формулу обратной прогонки (9), определяются последовательно значения Т_i для всех ;

в) пункты «а» и «б» повторяются до выполнения условия сходимости итераций 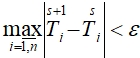, где ε – бесконечно малая величина, s – порядок итерации, т.е. проводятся локальные итерации, так как коэффициенты  являются нелинейными функциями температуры.

На каждом временном слое пункт II повторяется.

Данная разностная задача будет вполне определенной, если указать способ выбора параметров сглаживания, который играет определенную роль в точности решения.

Коэффициенты  разностного уравнения (7) вычисляются в зависимости от значения температуры по выражениям (2) и (3). Теплота фазового превращения, выделяющаяся или поглощающаяся на фазовом фронте, учитывается в выражении теплоемкости , определенном в интервале сглаживания. Если в указанный интервал не попадет ни одно узловое значение температуры, то температурное поле будет определено без учета выделения или поглощения теплоты на фронте. Следовательно, возникает условие выбора длины интервала сглаживания: параметры сглаживания должны быть выбраны так, чтобы на каждом временном шаге интервал сглаживания определялся значениями температур хотя бы в двух соседних узлах, между которыми находится фронт фазового превращения (сглаживание в пределах одной пространственной ячейки).

Если фазовый фронт находится между пространственными узлами x_i-1 и x_i, то должны выполняться следующие условия:

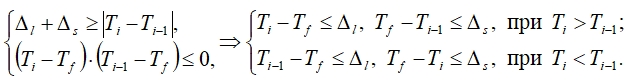
где Т_i и Т_i-1 – значения температуры в узлах х_i и х_i-1 соответственно.

Для оценки точности конечно-разностной схемы, разработанной на основе метода Самарского-Моисеенко, было проведено сравнение результатов численного расчета с точным автомодельным решением задачи протаивания неограниченного массива грунта при постоянных температурах на границах [8]. Численная модель данной одномерной задачи реализуется на языке программирования «Pascal», при этом величина радиуса теплового влияния берется наибольшей, т.к. аналитическое решение получено для полупространства. Эта задача имеет точное автомодельное решение, а коэффициент пропорциональности в законе движение границы фазового перехода найден с помощью пакета программ «MathCad Professional».

Расчеты были проведены при следующих входных данных:

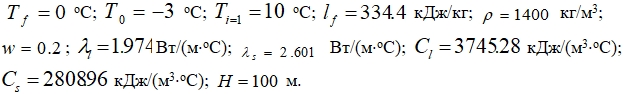
Оказалось, что наибольшая относительная погрешность вычисления координаты фазового превращения наблюдается, если сглаживание проводить в пределах одной пространственной ячейки. Эта погрешность значительно понижается, если фазовая область охватывает больше двух узлов. Очевидно, что в начале процесса протаивания не могут выполняться условия выбора интервала сглаживания, поэтому в эти моменты времени сглаживание можно проводить в пределах одной пространственной ячейки или ограничиться несколькими узлами. При симметричности половинок интервала сглаживания получается, что количества узлов, охватываемых областью фазового превращения как со стороны жидкой, так и твердой фаз будут неодинаковыми. Для задачи протаивания число узлов, входящих в интервал сглаживания со стороны жидкой фазы меньше, чем со стороны твердой.

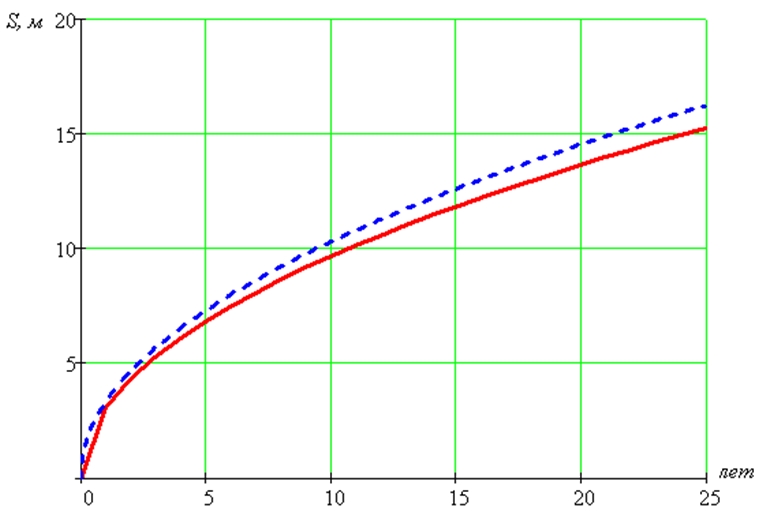
На рис. 2 показана динамика движения фазового фронта. При этом число узлов, входящих в интервал сглаживания со стороны жидкой фазы равно 3, а со стороны твердой – 5. Видно, что с течением времени скорость движения фазового фронта уменьшается из-за малой теплоинерционности талого грунта. Некоторое различие между результатами объясняется тем, что в точном автомодельном решении в отличие от численного массив грунта считается неограниченным, то есть для движения фронта промерзания создаются как бы благоприятные условия.

Рис. 2 – Изменение координаты фазового фронта с течением времени:

сплошная линия – точное автомодельное решение; штриховая – численное

 

Сравнение точного автомодельного и численного решений позволяет сделать вывод о правильности разработанной конечно-разностной схемы математической модели и вычислительного алгоритма.

На основе вышеописанного алгоритма был разработан программный комплекс на языке программирования Delphi7, обладающим широким набором сервисных программ, обеспечивающих вывод таблиц, изолиний, отображающих динамику процесса теплообмена. Разработанный комплекс программ, подтвердил свою работоспособность и эффективность на многочисленных расчетах теплового состояния рассматриваемого тела.

В таблице 1 даны среднемесячные значения температуры воздуха (Т_в), скорости ветра (υ_в) [5], [8] и суммарной солнечной радиации для условий г. Якутска (Q_c) [9]. Значения этих величин между месяцами были аппроксимированы линейными зависимостями. Физические характеристики слоев грунтов приведены в таблице 2. Здесь теплофизические свойства грунтов приняты по нормативным значениям, представленными заказчиком; а свойства бетона и пенополистирола приняты по [10], [11]. В табл. 3 представлены натурные данные температурного поля по глубине массива грунтов.

 

Таблица 1 – Среднемесячные значения температуры воздуха, скорости ветра и суммарной солнечной радиации

Параметры	Январь	Февраль	Март	Апрель	Май	Июнь
Тв, оС	-42,6	-35,9	-22,2	-7,2	5,8	15,4
υв, м/с	1.4	1,4	2,0	2,8	3,4	3,3
Qc, Вт/м2	14,188	48,363	120,594	192,515	211,320	244,213
Параметры	Июль	Август	Сентябрь	Октябрь	Ноябрь	Декабрь
Тв, оС	18,7	14,.9	6,2	-8,0	-28,3	-39,5
υв, м/с	3,0	2,8	2,6	2,6	2,0	1,3
Qc, Вт/м2	225,134	165,771	106,867	51,523	21,219	7,841

 

Таблица 2 – Характеристики слоев многослойного массива насыпи и ее грунтового основания

№	Вид слоя	Толщина, м	Плотность, кг/м3	Влажность	Температура фазового перехода, оС	Коэффициент теплоемкости, Вт/(м×оС)		Объемная теплоемкость C×10-6, Дж/(м3×оС)
						ll	ls	Сl	Сs
1	Армобетон	0,24	2500	0,00	0,00	2,04	2,04	2,100	2,100
2	Цементобетон	0,24	2500	0,00	0,00	2,04	2,04	2,100	2,100
3	Насыпной грунт (песок средней крупности)	0,67	1880	0,17	0,80	1,814	2,035	2,472	2,015
4	Пенополи-стирол	0,08	150	0,00	0,00	0,06	0,06	0,201	0,201

 

Таблица 3 – Значения температур по глубине массива грунтов в середине мая

х, м	0	1	2	3	4	5	6
Т, оС	-1,0	-1,4	-2,0	-2,8	-3,9	-4,15	-4,05
х, м	7	8	9	10	11	12	13
Т, оС	-3,8	-3,55	-3,25	-2,75	-2,5	-2,1	-1,9
х, м	14	15	16	17	18	19	20
Т, оС	-1,5	-1,3	-1,2	-1,2	-1,2	-1,2	1,2

Примечание: при температуре воздуха 0⁰С  

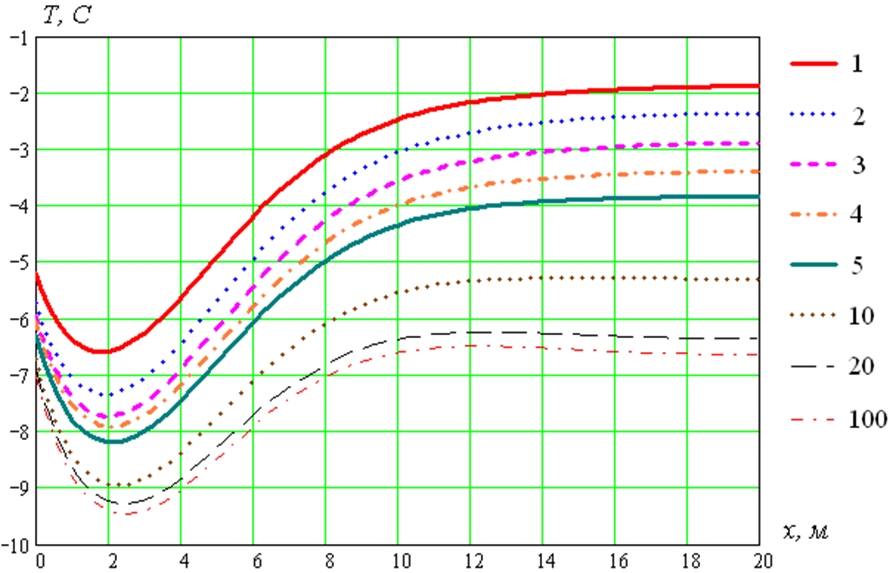
В результате получены температурные поля массива грунтов под насыпью полосы взлета и посадки в различные моменты времени в основании ВПП (насыпь толщиной 1,24 м): армобетон и цементобетон толщиной 0,48 м, насыпной грунт толщиной 0,68 м, пенополистирол толщиной 0,08 м (см. рисунки 3 и 4). В расчетных данных взят май месяц [11].

Рис. 3 – Распределение температуры грунтов под насыпью по глубине в мае

Примечание: цифры у кривых соответствуют годам

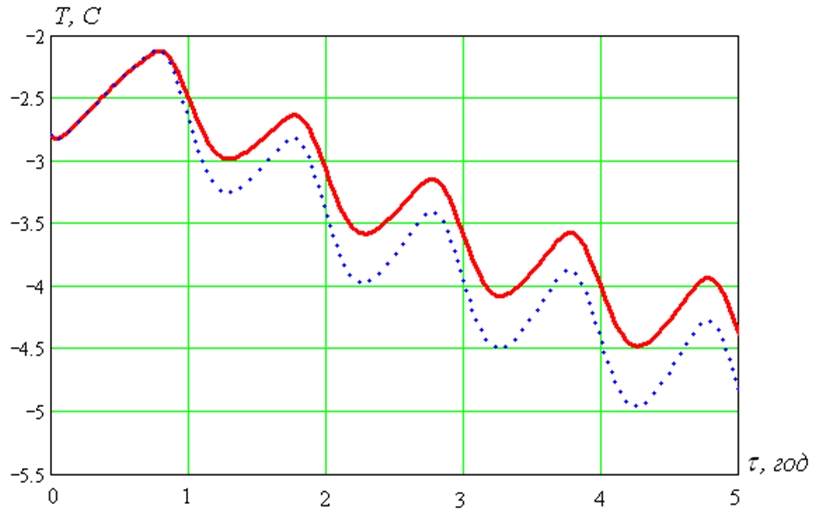
Рис. 4 – Динамика изменения температуры массива грунтов на глубине z = 10 м:

сплошная кривая – при толщине изоляции 0,08 м; штриховая – при толщине 0.04 м

  В таблице 4 приведена рассчитанная глубина сезонного оттаивания грунтов под насыпью в середине октября (м).  

Таблица 4 – Глубина сезонного оттаивания грунтов под насыпью

Год	1 вариант насыпи высотой 1.24 м		2 вариант насыпи высотой 1.20 м
	с изоляцией (0.08 м)	без изоляции	с изоляцией (0.04 м)	без изоляции
1	0.52	1.47	0.79	1.52
2	0.38	1.11	0.62	1.24
3	0.36	1.07	0.61	1.15
4	0.34	1.05	0.59	1.14
5	0.33	1.03	0.58	1.10
10	0.29	1.00	0.54	1.00
20	0.28	0.96	0.53	0.99
100	0.26	0.95	0.51	0.98

 

Укладка теплоизоляции в основание насыпи позволяет существенно уменьшить глубину оттаивания массива, тем самым, снизить объемы земляных работ при строительстве за счет уменьшения высоты насыпи, а также увеличить теплоустойчивость массива. Небольшая насыпь приводит к сокращению срока и снижению стоимости строительства.

Анализ результатов вычислительного эксперимента (опытные данные не могут быть получены в следствие ремонта ВПП на данный момент) показал, что применение слоя теплоизоляции в теплый период года в основание взлетно-посадочной полосы способствует затуханию нестационарных тепловых возмущений. Теплоизоляцию в основание ВВП полосы рекомендуется проложить в зимнее время, что будет способствовать аккумуляции холода в массиве, увеличить несущую способность полосы и продлить срок ее эксплуатации. 

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Велли Ю.Я. Справочник по строительству на вечномерзлых грунтах / Ю.Я. Велли, В.И. Докучаева, Н.Ф. Федорова. – Л.: Стройиздат, 1977. - 552 с.
2. Тихонов А.Н. Уравнения математической физики / А.Н. Тихонов, А.А. Самарский. – М.: Наука, 1977. - 736 с.
3. Самарский А.А. Экономичная схема сквозного счета для многомерных задач Стефана / А.А. Самарский, Б.Д. Моисеенко // Журнал вычислительной математики и математической физики. – 1965. - Т. 5. - № 5. - С. 816–827.
4. Будак Б.М. Разностный метод со сглаживанием коэффициентов для решения задачи Стефана / Б.М. Будак, Е.Н. Соловьева, А.Б. Успенский // Журнал вычислительной математики и математической физики. 1965. - Т. 5. - № 5. - С. 828–840.
5. Павлов А.В. Теплообмен почвы с атмосферой в северных и умеренных широтах территории СССР / А.В. Павлов. – Якутск: Якутское книжное изд-во, 1975. - 304 с.
6. Калиткин Н.Н. Численные методы. / Н.Н. Калиткин. – М: Наука, 1978. – 512 с.
7. Самарский А.А. Методы решения сеточных уравнений. / А.А. Самарский, Е.С. Николаев. – М: Наука, 1978. – 592 с.
8. Гаврилова М.К. Климат Центральной Якутии / М.К. Гаврилова. – Якутск: Якутское книжное изд-во, 1973. - 120 с.
9. СНиП 23-01-99. Строительная климатология. Госстрой России. – М.: ГУПП ЦПП, 2000. – 59 с.
10. СНиП II-3-79*. Строительная теплотехника. Госстрой России. – М.: ГУПП ЦПП, 1998. – 29 с.
11. Порхаев Г.В. Прогнозирование температурного режима вечномерзлых грунтов на застраиваемых территориях / Г.В. Порхаев, В.К. Щелоков. – Л.: Стройиздат, 1980. - 112 с.
12. Федоров А.Н. Спасская падь / А.Н. Федоров, Т.Х. Максимов, П.П. Гаврильев и др. // Комплексные исследования мерзлотных ландшафтов. – Якутск: Издательство Института мерзлотоведения СО РАН, 2006. - 210 с.

Список литературы на английском языке / References in English

1. Velli Ju.Ja. Spravochnik po stroitel'stvu na vechnomerzlyh gruntah [Handbook of construction on permafrost soils] / Ju.Ja. Velli, V.I. Dokuchaeva, N.F. Fedorova. – L.: Strojizdat, 1977. - 552 p. [in Russian]
2. Tihonov A.N. Uravnenija matematicheskoj fiziki [Equations of mathematical physics]/ A.N. Tihonov, A.A. Samarskij. – M.: Nauka, 1977. - 736 p. [in Russian]
3. Samarskij A.A. Jekonomichnaja shema skvoznogo scheta dlja mnogomernyh zadach Stefana [Cost-effective end-to-end counting scheme for multidimensional Stefan problems] / A.A. Samarskij, B.D. Moiseenko // Zhurnal vychislitel'noj matematiki i matematicheskoj fiziki [Journal of Computational Mathematics and Mathematical Physics]. – 1965. - Vol. 5. - № 5. - 816–827. [in Russian]
4. Budak B.M. Raznostnyj metod so sglazhivaniem kojefficientov dlja reshenija zadachi Stefana [Difference method with smoothing coefficients for solving the Stefan problem] / B.M. Budak, E.N. Solov'eva, A.B. Uspenskij // Zhurnal vychislitel'noj matematiki i matematicheskoj fiziki [Journal of Computational Mathematics and Mathematical Physics]. 1965. - Vol. 5. - № 5. - P. 828–840. [in Russian]
5. Pavlov A.V. Teploobmen pochvy s atmosferoj v severnyh i umerennyh shirotah territorii SSSR [Heat exchange of the soil with the atmosphere in the northern and temperate latitudes of the territory of the USSR] / A.V. Pavlov. – Jakutsk: Jakutsk publishing house, 1975. - 304 p. [in Russian]
6. Kalitkin N.N. Chislennie metody [Numerical methods] / N.N. Kalitkin. – M. Nauka, 1978. – 512 p.
7. Samarskij A.A. Metody reshenija setochnyh uravnenij. [Methods for solving grid equations] / A.A. Samarskij, E.S. Nikolaev. – M. Nauka, 1978. – 592 p.
8. Gavrilova M.K. Klimat Central'noj Jakutii [Climate of Central Yakutia] / M.K. Gavrilova. – Jakutsk: Jakutsk publishing house, 1973. - 120 p. [in Russian]
9. SNiP 23-01-99. Stroitel'naja klimatologija. Gosstroj Rossii [Construction climatology. Gosstroy of Russia]. – M.: GUPP CPP, 2000. – 59 p. [in Russian]
10. SNiP II-3-79*. Stroitel'naja teplotehnika. Gosstroj Rossii [Construction heat engineering. Gosstroy of Russia]. – : GUPP CPP, 1998. – 29 p. [in Russian]
11. Porhaev G.V. Prognozirovanie temperaturnogo rezhima vechnomerzlyh gruntov na zastraivaemyh territorijah [Forecasting of the temperature regime of permafrost soils in the built-up areas] / G.V. Porhaev, V.K. Shhelokov. – L.: Strojizdat, 1980. - 112 p. [in Russian]
12. Fedorov A.N. Spasskaja pad' [Spasskaya Pad] / A.N. Fedorov, T.H. Maksimov, P.P. Gavril'ev et al. // Kompleksnye issledovanija merzlotnyh landshaftov [Complex studies of permafrost landscapes]. - Yakutsk: Publishing House of the Institute of Permafrost Studies SB RAS], 2006. - 210 p. [in Russian]