АППРОКСИМАЦИЯ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК И СИНТЕЗ ПО НИМ РАДИОТЕХНИЧЕСКИХ ФИЛЬТРОВ ВЫСОКОГО ПОРЯДКА НА ОСНОВЕ ПОЛИНОМОВ ЛЕЖАНДРА, ГЕГЕНБАУЭРА И ЯКОБИ

АППРОКСИМАЦИЯ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК И СИНТЕЗ ПО НИМ РАДИОТЕХНИЧЕСКИХ ФИЛЬТРОВ ВЫСОКОГО ПОРЯДКА НА ОСНОВЕ ПОЛИНОМОВ ЛЕЖАНДРА, ГЕГЕНБАУЭРА И ЯКОБИ

Научная статья

Буренко Е.А.*

ORCID: 0000-0003-0660-0843,

Московский авиационный институт (Национальный исследовательский университет), Москва, Россия

* Корреспондирующий автор (super.evgeny-burenko2012[at]yandex.ru)

Аннотация

Повышение качества фильтрации радиосигналов актуально для радиотехнических систем различного назначения. Разработчики радиоэлектронной аппаратуры достаточное внимание уделяют улучшению характеристик радиотехнических частотно-избирательных фильтров. Они находят широкое применение в системах телеметрии, телеуправления, в измерительной и вычислительной технике, в радиотехнической, физической, медицинской и другой различной аппаратуре. Как правило, при выборе аппроксимации амплитудно-частотной характеристики фильтра, предпочтение отдаётся степенным функциям (фильтры Баттерворта) и полиномам Чебышёва I рода. Целью настоящей статьи является анализ предлагаемых методов аппроксимации амплитудно-частотных характеристик фильтров высокого порядка, основанных на использовании полиномов Лежандра, Гегенбауэра и Якоби, а также исследование возможности физической реализации радиотехнических фильтров с улучшенными амплитудно-частотными характеристиками при использовании математического аппарата аппроксимации на указанных полиномах.

Ключевые слова: синтез радиотехнических фильтров, амплитудно-частотная характеристика (АЧХ), передаточная функция, полиномиальная аппроксимация, оптимально монотонная аппроксимация, полиномы Лежандра, полиномы Гегенбауэра, полиномы Якоби.

AN APPROXIMATION OF THE AMPLITUDE AND FREQUENCY CHARACTERISTICS AND SYNTHESIS OF HIGH-ORDER RADIO FILTERS BASED ON LEGENDRE, GEGENBAUER, AND JACOBI POLYNOMIALS

Research article

Burenko E.A.*

ORCID: 0000-0003-0660-0843,

Moscow Aviation Institute (National Research University), Moscow, Russia

* Corresponding author (super.evgeny-burenko2012[at]yandex.ru)

Abstract

Improving the quality of radio signal filtering is important for radio engineering systems for various purposes. The developers of radio-electronic equipment pay sufficient attention to improving the characteristics of radio-technical frequency-selective filters. They are widely used in telemetry and remote control systems, in measuring and computing equipment, in radio engineering, physical, medical, and other various types of equipment. As a rule, when choosing an approximation of the amplitude-frequency response of the filter, preference is given to power functions (Butterworth filters) and Chebyshev polynomials of the first kind. The purpose of this article is to analyze the proposed methods for approximating the amplitude-frequency characteristics of high-order filters based on the use of Legendre, Gegenbauer, and Jacobi polynomials as well as to study the possibility of the physical implementation of radio-technical filters with improved amplitude-frequency characteristics using the mathematical apparatus of approximation on these polynomials.

Keywords: synthesis of radio-technical filters, Frequency response, transfer function, polynomial approximation, optimal monotone approximation, Legendre polynomials, Gegenbauer polynomials, Jacobi polynomials.

Задача синтеза фильтра состоит из нескольких этапов:

- выбор аппроксимирующей функции для заданной характеристики фильтра;

-построение передаточной функции фильтра в соответствии с аппроксимирующей функцией (любую характеристику фильтра как четырёхполюсника можно свести к передаточной функции и наоборот);

- конструирование фильтра и анализ его характеристик.

В теории электрических фильтров во всех методах аппроксимации АЧХ используется не сама АЧХ, а квадрат модуля комплексной частотной характеристики , т. е. квадрат АЧХ – , либо функция, обратная квадрату АЧХ 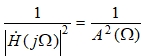. Это объясняется тем, что функция , являясь вещественной функцией вещественного аргумента, упрощает решение задачи аппроксимации, поскольку исключает на этапе аппроксимации чрезвычайно сложные, а порой невыполнимые операции над функциями комплексного переменного. Для нормированного фильтра нижних частот функция квадрата АЧХ в общем случае представляется в виде [1], [2], [4]:

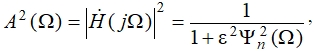    (1)

где Ψ_n(Ω) – аппроксимирующая функция степени n, называемая также функцией фильтрации, 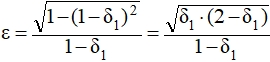 – параметр, управляющий неравномерностью АЧХ в полосе пропускания (реже, например, при дробно-рациональной аппроксимации – в полосе задерживания). В общем случае Ψ_n(Ω) – это дробно-рациональная функция с вещественными коэффициентами (в частности полином), удовлетворяющая условиям:  в полосе пропускания и  вне полосы пропускания фильтра.

Порядок фильтра n определяется из условия A(Ω_k) ≤ δ₂ и вычисляется методом подбора значений n до тех пор, пока не выполнится данное условие.

В зависимости от вида аппроксимирующей функции получают различные типы фильтров. Если в качестве аппроксимирующей функции используются полиномы, то фильтры называются полиномиальными [1], [2], [3], [4]. Среди полиномиальных фильтров наиболее широкое применение нашли фильтры Баттерворта и Чебышёва I рода. Если Ψ_n(Ω) – дробно-рациональная функция, например, дробь Золотарёва F_n(Ω), получаемая непосредственно из эллиптической дробно-рациональной функции Якоби R_n(Ω), то получается фильтр Золотарёва–Кауэра, называемый также просто фильтром Кауэра, фильтром Золотарёва или эллиптическим фильтром. Среди дробно-рациональных фильтров помимо фильтров Золотарёва–Кауэра известны также фильтры Чебышёва II рода и дробные фильтры Чебышёва [1], [2], [3], [6].

Фильтры Баттерворта наиболее полно соответствуют условиям безыскажённой передачи сигнала по амплитуде и фазе. При прочих равных условиях фильтр Баттерворта имеет более высокий порядок, чем фильтры других типов [1], [2].

Фильтры Чебышёва I рода обладают равноволновой неравномерностью АЧХ в полосе пропускания, но при этом имеют бóльшую крутизну спада характеристики в переходной полосе, чем фильтры Баттерворта [1], [2], [3]. Другими словами, коэффициент прямоугольности фильтра Чебышёва больше, чем у фильтра Баттерворта при одинаковых заданных требованиях к АЧХ.

Фильтры Чебышёва I рода используются в тех случаях, когда требуется большáя скорость затухания вне полосы пропускания и не предъявляются жёсткие требования по обеспечению минимальных искажений АЧХ в полосе пропускания. По этой причине фильтры Чебышёва наиболее широко применяются в радиосистемах для подавления помех от соседних радиостанций [1], [2].

Аппроксимация амплитудно-частотной характеристики фильтра полиномами Лежандра

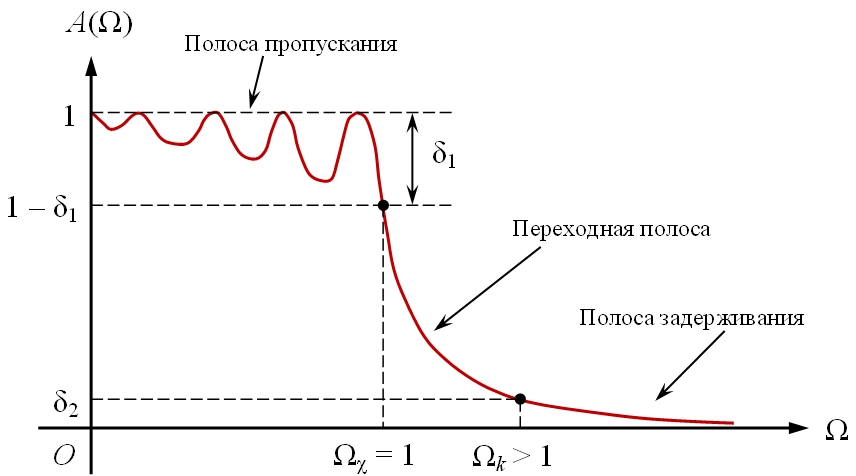
Если в качестве аппроксимирующей функции Ψ_n(Ω) использовать предлагаемые в работе полиномы Лежандра, то получим соответственно фильтр с амплитудно-частотной характеристикой на полиномах Лежандра (рис. 1).

Как уже было показано ранее, Ψ_n(Ω) – это дробно-рациональная функция с вещественными коэффициентами, удовлетворяющая условиям:  в полосе пропускания и  вне полосы пропускания фильтра. Полином Лежандра n-го порядка удовлетворяет этим условиям, следовательно, его можно использовать в качестве аппроксимирующей функции.

Функция квадрата АЧХ нормированного фильтра нижних частот с аппроксимацией на полиномах Лежандра n-го порядка имеет вид:

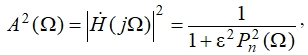    (2)

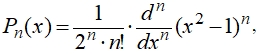где  – полином Лежандра n-го порядка, ε – параметр, отвечающий за пульсации в полосе пропускания. Полином Лежандра степени n можно выразить через формулу Родрига в виде [7]:      (3) однако более удобно использовать представление через сумму: 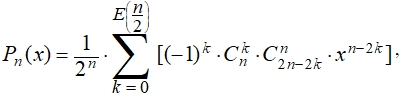   (4) где E – оператор выбора целой части от 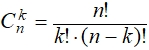 – число сочетаний из n элементов по k. Раскрывая сочетания, можно записать более подробно: 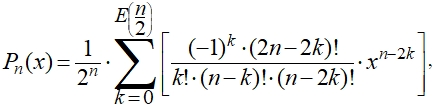    (5)  

Рис. 1 – Вид амплитудно-частотной характеристики нормированного фильтра нижних частот, аппроксимированной полиномом Лежандра

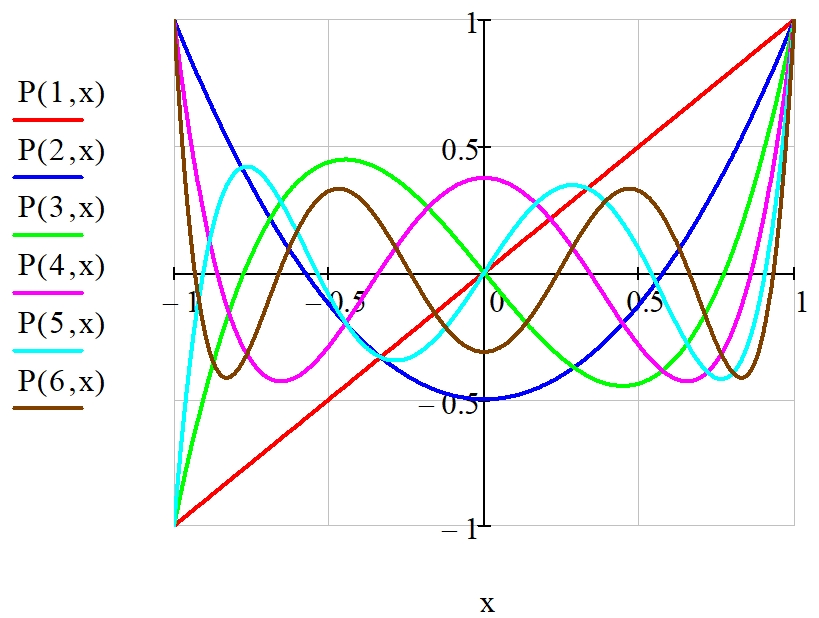
  Графики полиномов Лежандра 1 ÷ 6-го порядков приведены на рис. 2. Полюсы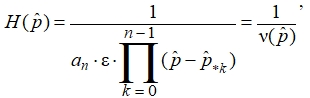  передаточной функции определяются, исходя из решения уравнения:      (6) Передаточная функция фильтра, с учётом того, что образующие её полюсы лежат в левой p-полуплоскости, определяется следующим образом:       (7) где 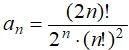 – коэффициент полинома Лежандра n-го порядка при старшей степени аргумента,  – полином знаменателя, который является полиномом Гурвица.  

Рис. 2 – Графики полиномов Лежандра 1 ÷ 6-го порядков

На основании выражения (7) производится реализация фильтра на выбранной элементной базе – это пассивные LC-фильтры [1], [2], [3], либо – активные RC-фильтры. Возможность реализации активных RC-фильтров на предлагаемом методе аппроксимации АЧХ показана в работе [4].

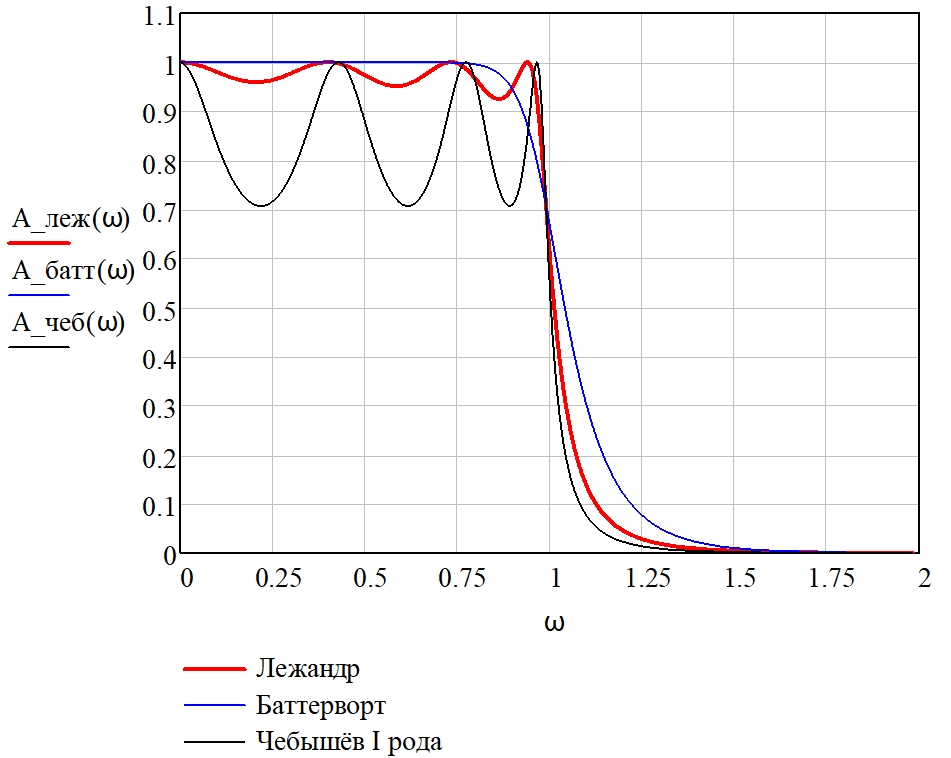
На рис. 3 приведено сравнение амплитудно-частотных характеристик фильтров, аппроксимированных полиномами Лежандра, степенными функциями Баттерворта и полиномами Чебышёва I рода при одинаковых заданных требованиях к фильтру. Допустимое отклонение значения АЧХ от единицы в полосе пропускания равно δ₁ = 1 –  ≈ 0,293 (что соответствует максимальному затуханию α_max ≈ 3,01 дБ), допустимое отклонение значения АЧХ от нуля в полосе задерживания равно δ₂ = 0,0005 (что соответствует минимальному затуханию α_min ≈ 66,02 дБ), нормированное значение граничной частоты полосы задерживания равно Ω_k = 2. При этом соответствующие порядки фильтров равны: n_батт. = 11, n_чеб. = 7, n_леж. = 7.

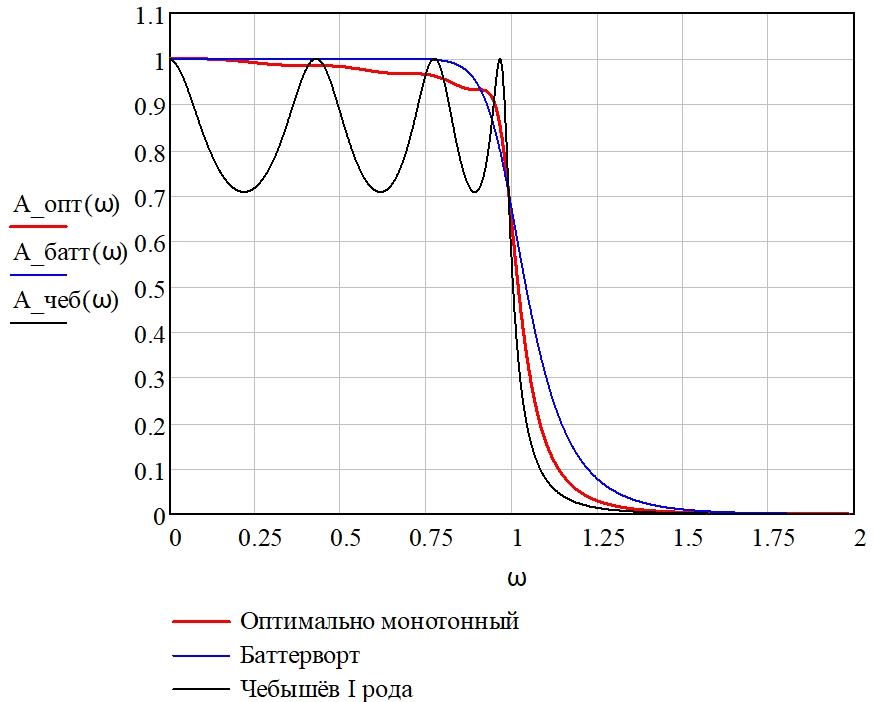
Рис. 3 – Амплитудно-частотные характеристики нормированного фильтра нижних частот, аппроксимированные полиномами Лежандра, степенными функциями Баттерворта и полиномами Чебышёва I рода

 

Из полученных результатов следует, что при одинаковых δ₁, δ₂ и Ω_k амплитуда пульсаций АЧХ при использовании полинома Лежандра значительно меньше, чем при использовании полинома Чебышёва I рода (однако порядки фильтров оказываются равными n_чеб. = 7, n_леж. = 7), а также полином Лежандра позволяет получить более высокую крутизну спада АЧХ за пределами полосы пропускания, чем степенная функция Баттерворта, при этом обеспечивается выигрыш в порядке фильтра: n_батт. = 11, а n_леж. = 7.

Оптимально монотонная аппроксимация амплитудно-частотной характеристики фильтра

Функция квадрата АЧХ фильтра n-го порядка определяется выражением:

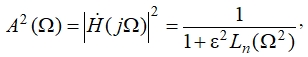     (8)

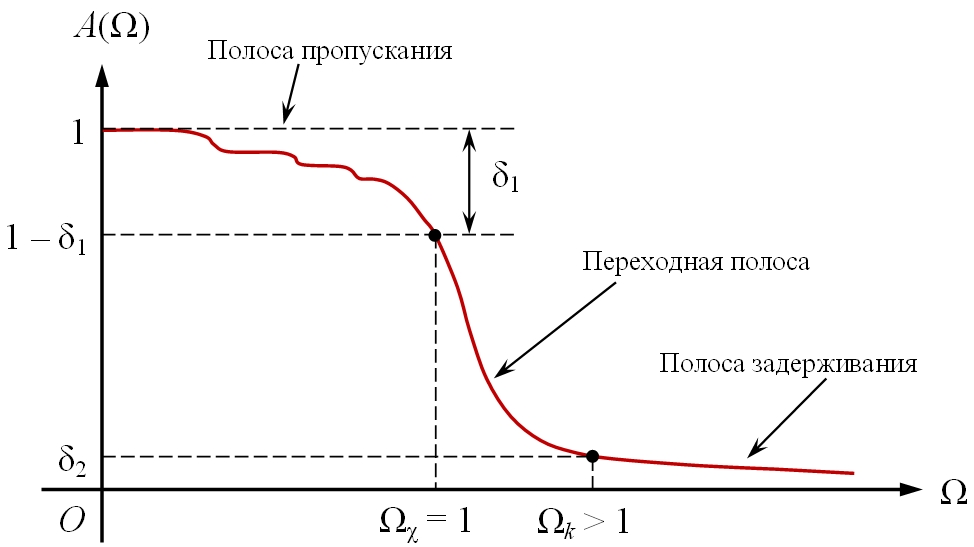
где ε – параметр, отвечающий за неравномерность в полосе пропускания, L_n(Ω²) – аппроксимирующий полином n-го порядка, который характеризуется выполнением ряда специальных критериев, обеспечивающих желаемые качества характеристик фильтра, а именно, монотонность АЧХ в полосе пропускания и крутой спад АЧХ за пределами полосы пропускания (рис. 4).

Рис. 4 – Вид амплитудно-частотной характеристики нормированного фильтра нижних частот с оптимально монотонной аппроксимацией

  Выражение для аппроксимирующего полинома L_n(Ω²) нечётного порядка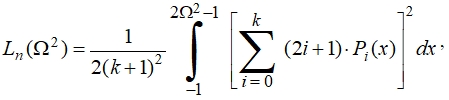 имеет вид:     (9) где n = 2k + 1 – порядок полинома, P_i(x) – полином Лежандра i-го порядка, i = 0, 1, 2, …, k. Соответственно, для n чётного, полином L_n(Ω²) имеет вид: 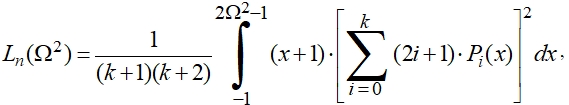     (10) где n = 2k + 2 – порядок полинома, 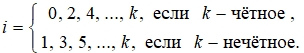 Результат вычислений С помощью выражений (9) и (10) получены аппроксимирующие полиномы L_n(Ω²) фильтров 1 ÷ 6-го порядков (табл. 1).  

Таблица 1 – Аппроксимирующие полиномы L_n(Ω²) 1 ÷ 6-го порядков и значения коэффициента полинома при старшей степени аргумента a_n

n	Ln(Ω2)	an
1	Ω2	1
2	Ω4	1
3	3Ω6 – 3Ω4 + Ω2	3
4	6Ω8 – 8Ω6 + 3Ω4	6
5	20Ω10 – 40Ω8 + 28Ω6 – 8Ω4 + Ω2	20
6	50Ω12 – 120Ω10 + 105Ω8 – 40Ω6 + 6Ω4	50

 

Графики аппроксимирующих полиномов фильтров 1 ÷ 6-го порядков приведены на рис. 5.

Оптимально монотонная аппроксимация сочетает в себе свойства аппроксимаций на степенных функциях Баттерворта и полиномах Чебышёва I рода. Она не столь равномерна в полосе пропускания, как степенная функция Баттерворта, но и не содержит пульсаций, характерных для полиномов Чебышёва. Фильтр с такой характеристикой является компромиссным (оптимальным) решением между фильтром Баттерворта и Чебышёва I рода. Более крутой спад АЧХ, чем у фильтра Баттерворта достигается за счёт ухудшения равномерности АЧХ в полосе пропускания [4].

Рис. 5 – Графики оптимально монотонных аппроксимирующих функций (полиномов) 1 ÷ 6-го порядков

 

Полюсы  передаточной функции фильтра определяются, исходя из решения уравнения:

   (11)

Передаточная функция фильтра, с учётом того, что образующие её полюсы лежат в левой p-полуплоскости, определяется как

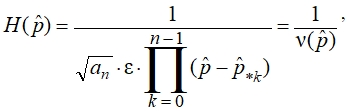     (12)

где a_n – коэффициент аппроксимирующего полинома n-го порядка при старшей степени аргумента (табл. 1),  – полином знаменателя, который является полиномом Гурвица.

На рис. 6 приведено сравнение амплитудно-частотных характеристик фильтров, аппроксимированных степенными функциями Баттерворта, полиномами Чебышёва I рода и методом оптимально монотонной аппроксимации при одинаковых заданных требованиях к фильтру. Допустимое отклонение значения АЧХ от единицы в полосе пропускания равно δ₁ = 1 – , допустимое отклонение значения АЧХ от нуля в полосе задерживания равно δ₂ = 0,0005, нормированное значение граничной частоты полосы задерживания равно Ω_k = 2. При этом соответствующие порядки фильтров равны: n_батт. = 11, n_чеб. = 7, n_опт. = 8.

Рис. 6 – Амплитудно-частотные характеристики нормированного фильтра нижних частот, аппроксимированные степенными функциями Баттерворта, полиномами Чебышёва I рода и методом оптимально монотонной аппроксимации

 

Как следует из рис. 6, фильтр с оптимально монотонной амплитудно-частотной характеристикой сочетает в себе свойства фильтров Баттерворта и Чебышёва I рода. Его АЧХ не столь равномерна в полосе пропускания, как у фильтра Баттерворта, но и не содержит пульсаций, характерных для фильтров Чебышёва. Более крутой спад амплитудно-частотной характеристики, чем у фильтра Баттерворта достигается за счёт ухудшения её равномерности в полосе пропускания.

Аналогично проведено сравнение амплитудно-частотных характеристик фильтров, аппроксимированных полиномами Лежандра и методом оптимально монотонной аппроксимации (рис. 7).

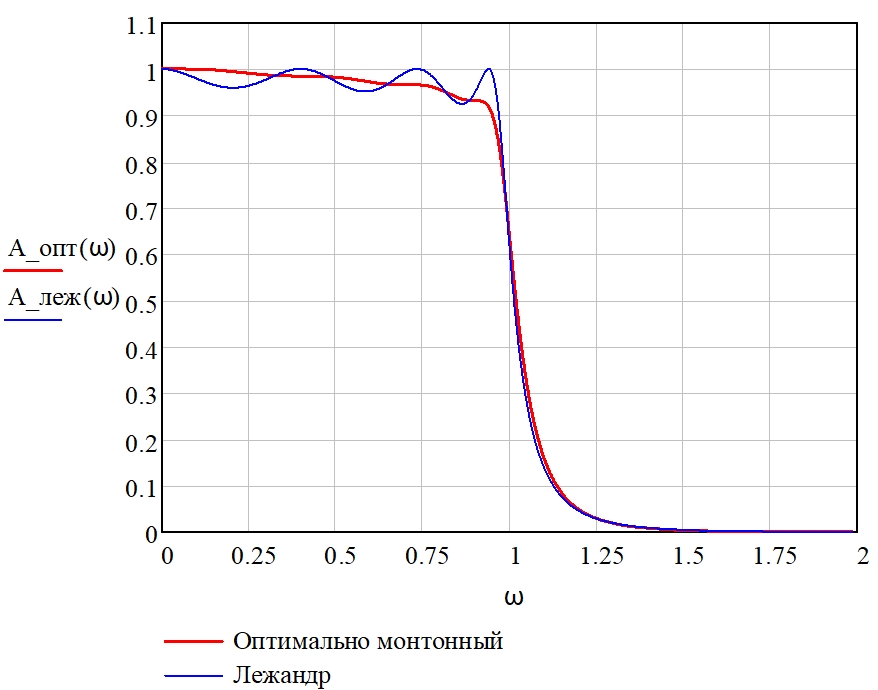
Рис. 7 – Амплитудно-частотные характеристики нормированного фильтра нижних частот, аппроксимированные полиномом Лежандра и методом оптимально монотонной аппроксимации

 

Как следует из рис. 7, одна и та же крутизна спада АЧХ обеспечивается полиномом Лежандра при порядке n_леж. = 7, и оптимально монотонной аппроксимирующей функцией при порядке n_опт. = 8. Наличие пульсаций при использовании полинома Лежандра уменьшает порядок фильтра, тогда как оптимально монотонная аппроксимация, являясь более равномерной, имеет порядок больший, чем при использовании полинома Лежандра.

Аппроксимация амплитудно-частотной характеристики фильтра полиномами Гегенбауэра

Полиномы Гегенбауэра степени n в общем случае представляются в виде [8]:

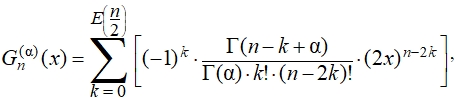    (13) где E – оператор выбора целой части от 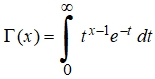,  – гамма-функция.

Как уже было показано ранее, для аппроксимации АЧХ фильтра, аппроксимирующая функция должна удовлетворять условиям:  в полосе пропускания и  вне полосы пропускания фильтра [4]. Это достигается при использовании полиномов Гегенбауэра , нормированных на некоторую постоянную величину :

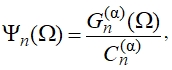   (14) которая определяется, как значение полинома Гегенбауэра при x = 1 и равна: 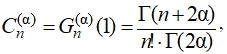    (15)

Для получения приемлемой формы АЧХ параметр α рекомендуется выбирать α > 0.

При α → 0 получившаяся функция Ψ_n(Ω) стремится к полиному Чебышёва I рода; при α = 0,5 она является полиномом Лежандра; при α = 1 – нормированным полиномом Чебышёва II рода, который может быть определён, как:

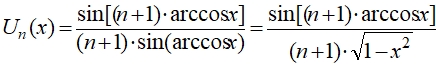, если –1 ≤ x ≤ 1, или для значений –1 > x > 1 выражением:  

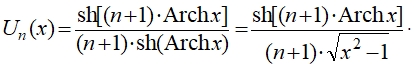
Также полиномы Гегенбауэра  являются частным случаем полиномов Якоби  при μ = ν = α – 0,5, которые будут рассмотрены далее.

Так как при 0 < α ≤ 0,5 полиномы Гегенбауэра являются обобщением полиномов Чебышёва I рода и Лежандра, то для получения более высокого качества избирательности фильтра, параметр полинома α рекомендуется выбирать α > 0,5.

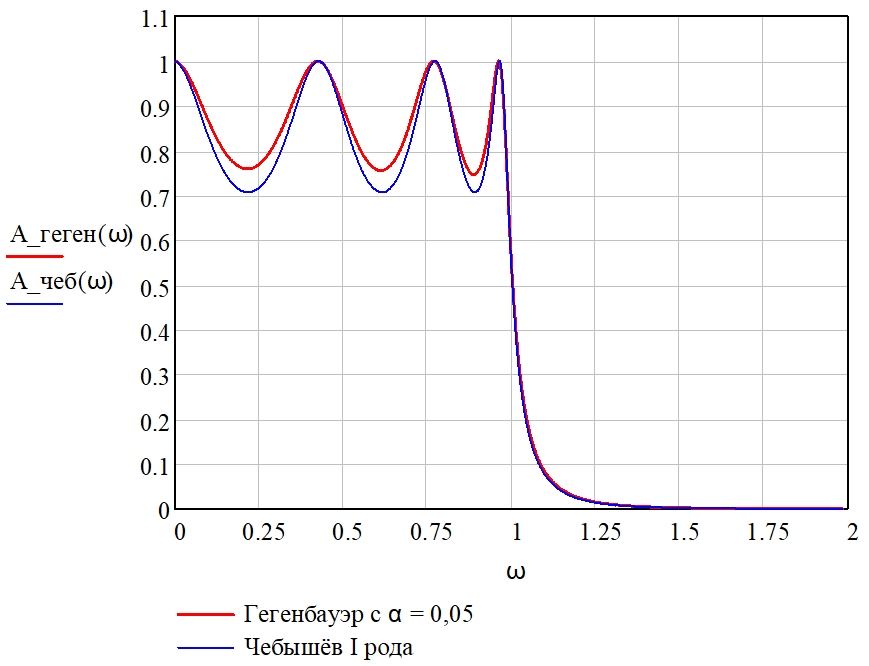
На рис. 8 приведено сравнение амплитудно-частотных характеристик (АЧХ) фильтров, аппроксимированных полиномами Чебышёва I рода и Гегенбауэра с параметром α = 0,05 при одинаковых заданных требованиях к фильтру. Допустимое отклонение значения АЧХ от единицы в полосе пропускания равно δ₁ = 1 –  ≈ 0,293, допустимое отклонение значения АЧХ от нуля в полосе задерживания равно δ₂ = 0,0005, нормированное значение граничной частоты полосы задерживания равно Ω_k = 2. При этом соответствующие порядки фильтров оказываются одинаковыми: n_чеб. = n_геген. = 7. Как следует из рис. 8, при α → 0, полином Гегенбауэра стремится к полиному Чебышёва I рода и достаточно высоких качеств избирательности не достигается. Характеристика по-прежнему является сильно пульсирующей.

Рис. 8 – Амплитудно-частотные характеристики нормированного фильтра нижних частот, аппроксимированные полиномами Чебышёва I рода и Гегенбауэра с параметром α = 0,05

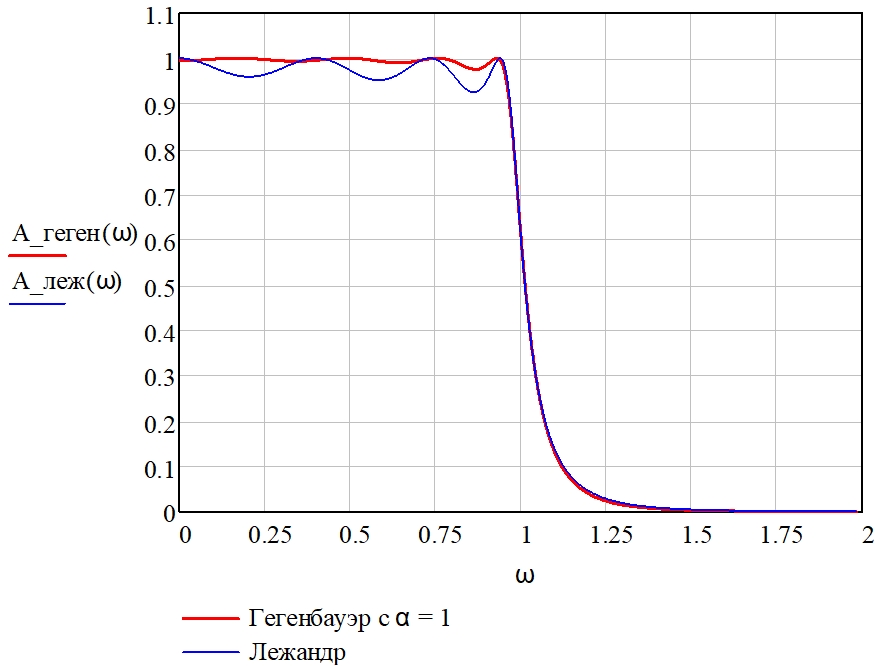
На рис. 9 приведено сравнение амплитудно-частотных характеристик (АЧХ) фильтров, аппроксимированных полиномами Лежандра и Гегенбауэра с α = 1 при одинаковых заданных требованиях к фильтру. Допустимое отклонение значения АЧХ от единицы в полосе пропускания равно δ₁ = 1 –  ≈ 0,293, допустимое отклонение значения АЧХ от нуля в полосе задерживания равно δ₂ = 0,0005, нормированное значение граничной частоты полосы задерживания равно Ω_k = 2. При этом соответствующие порядки фильтров равны: n_леж. = 7, n_геген. = 8. В данном случае при α = 1 величина пульсаций полинома Гегенбауэра значительно меньше, чем у полинома Лежандра, при этом крутизна спада характеристики фильтров практически одинакова. Недостатком полинома Гегенбауэра в данном случае является его более высокий порядок.

Рис. 9 – Амплитудно-частотные характеристики нормированного фильтра нижних частот,

аппроксимированные полиномами Лежандра и Гегенбауэра со значением α = 1

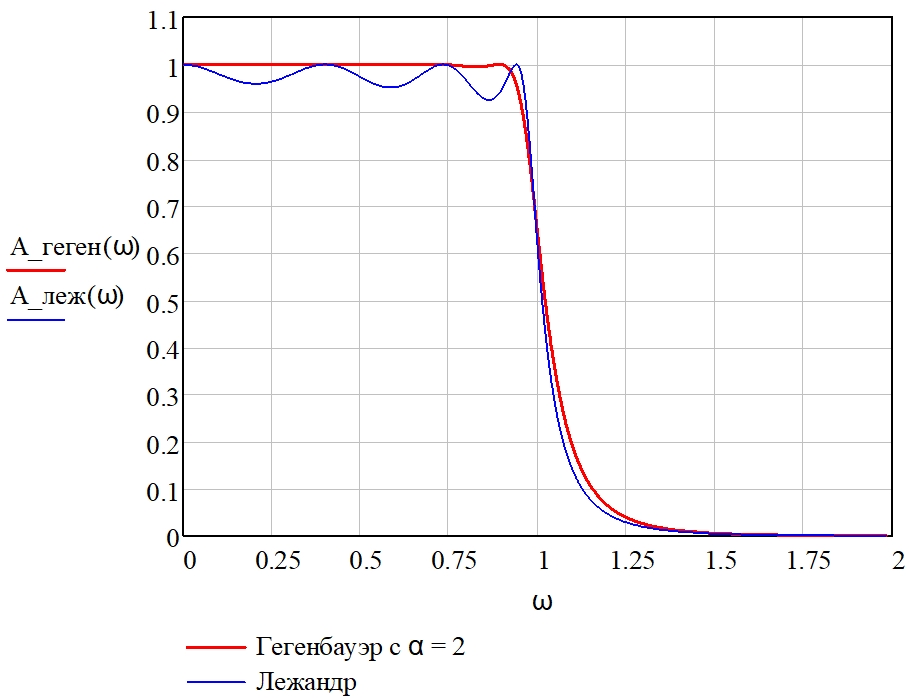
Аналогично проведено сравнение амплитудно-частотных характеристик фильтров, аппроксимированных полиномами Лежандра Гегенбауэра с α = 2 (рис. 10).

Рис. 10 – Амплитудно-частотные характеристики нормированного фильтра нижних частот, аппроксимированные полиномами Лежандра и Гегенбауэра со значением α = 2

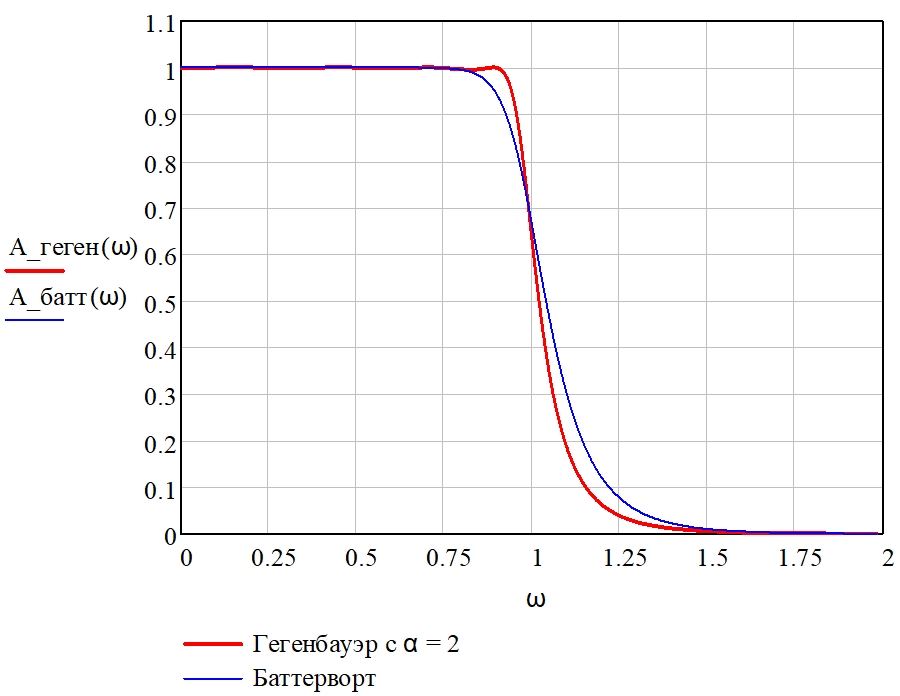
При значениях α > 1 также целесообразно провести сравнение амплитудно-частотных характеристик фильтров, аппроксимированных степенными функциями Баттерворта и полиномами Гегенбауэра (рис. 11). При этом полином Гегенбауэра с параметром α = 2 обеспечивает достаточно высокую равномерность АЧХ в полосе пропускания, а также доставляет характеристике фильтра более высокий спад за пределами полосы пропускания, чем функция Баттерворта. Соответствующие порядки полиномов имеют следующие значения: n_батт. = 11, n_геген. = 8, откуда видно, что полином Гегенбауэра имеет более низкий порядок, чем степенная функция Баттерворта.

Рис. 11 – Амплитудно-частотные характеристики нормированного фильтра нижних частот, аппроксимированные степенными функциями Баттерворта и полиномами Гегенбауэра с α = 2

Таким образом, на основе полиномов Гегенбауэра возможна реализация полиномиального фильтра n-го порядка с различными пульсациями АЧХ, величина которых зависит от параметра полинома α. Задавая параметр α из области рекомендуемых значений, можно получать фильтры с различными пульсациями АЧХ в полосе пропускания и различной крутизной АЧХ за её пределами, в частности, с улучшенной частотной избирательностью.

Аппроксимация амплитудно-частотной характеристики фильтра полиномами Якоби

Полиномы Якоби степени n в общем случае представляются в виде [9]:

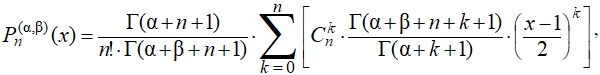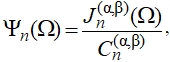    (16) где  – число сочетаний из n элементов по k, Г(x) – гамма-функция. Эти полиномы удовлетворяют условию ортогональности при α > –1 и β > –1. Для полиномов Якоби существует соотношение симметрии:     (17) Для получения аппроксимирующей функции необходимо использование так называемых модифицированных полиномов Якоби [9], [10]:     (18) нормированных на некоторую постоянную величину :     (19) которая определяется как значение модифицированного полинома Якоби при x = 1 и равна: 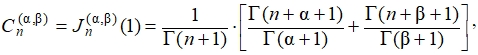    (20)

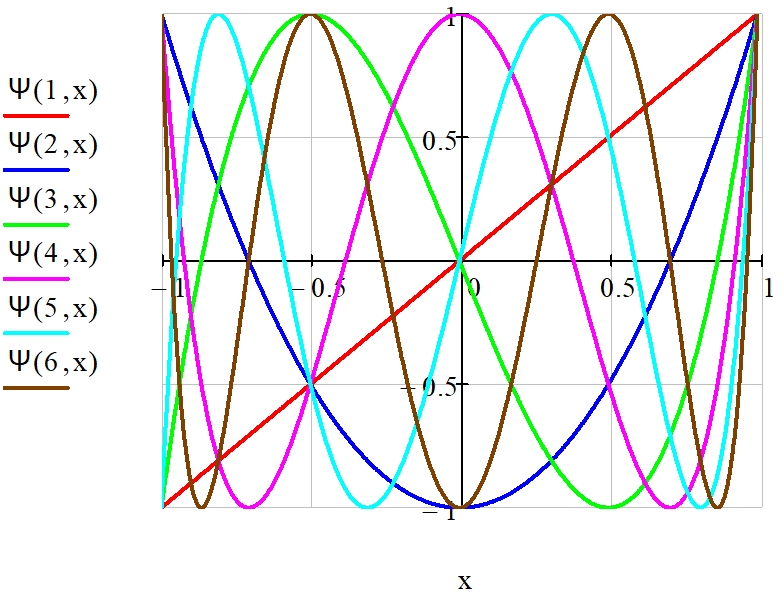
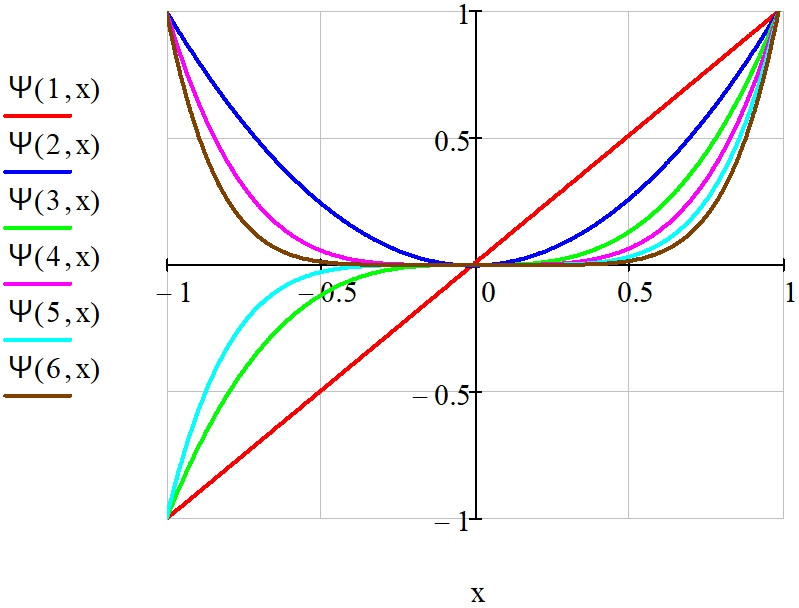
Многие известные ортогональные полиномы являются частными случаями нормированных модифицированных полиномов Якоби, например, при α = β = 0 функция Ψ_n(Ω) является полиномом Лежандра (рис. 2); при α = β = –0,5 – полиномом Чебышёва I рода (рис. 12); при α = β = 0,5 – нормированным полиномом Чебышёва II рода (рис. 13).

Рис. 12 – Графики функций Ψ_n(x) 1 ÷ 6-го порядков при α = β = –0,5

 

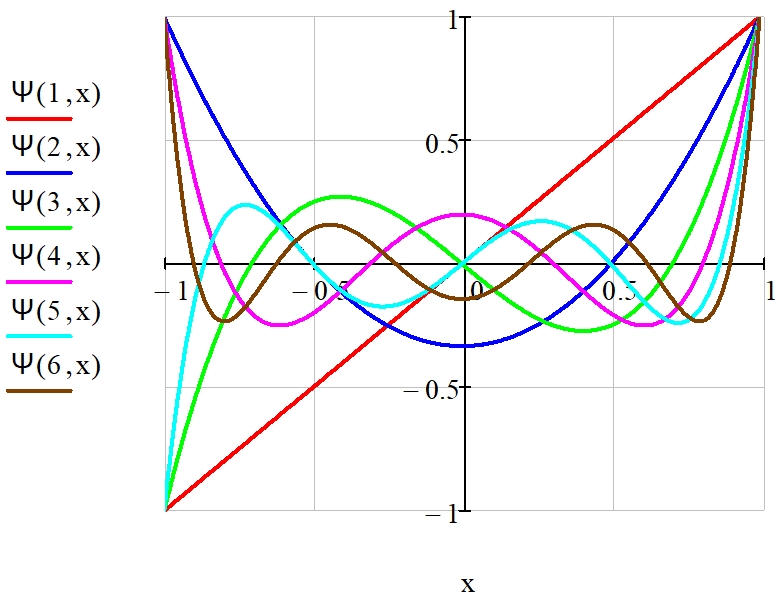
Кроме того, необходимо отметить тот факт, что при достаточно больших значениях α и β нормированный модифицированный полином Якоби в пределе стремится к степенной функции xⁿ, т. е. фильтр при таких значениях α и β будет представлять собой фильтр Баттерворта (рис. 14).

Рис. 13 – Графики функций Ψ_n(x) 1 ÷ 6-го порядков при α = β = 0,5

Рис. 14 – Графики функций Ψ_n(x) 1 ÷ 6-го порядков при α = 70 и β = 80

 

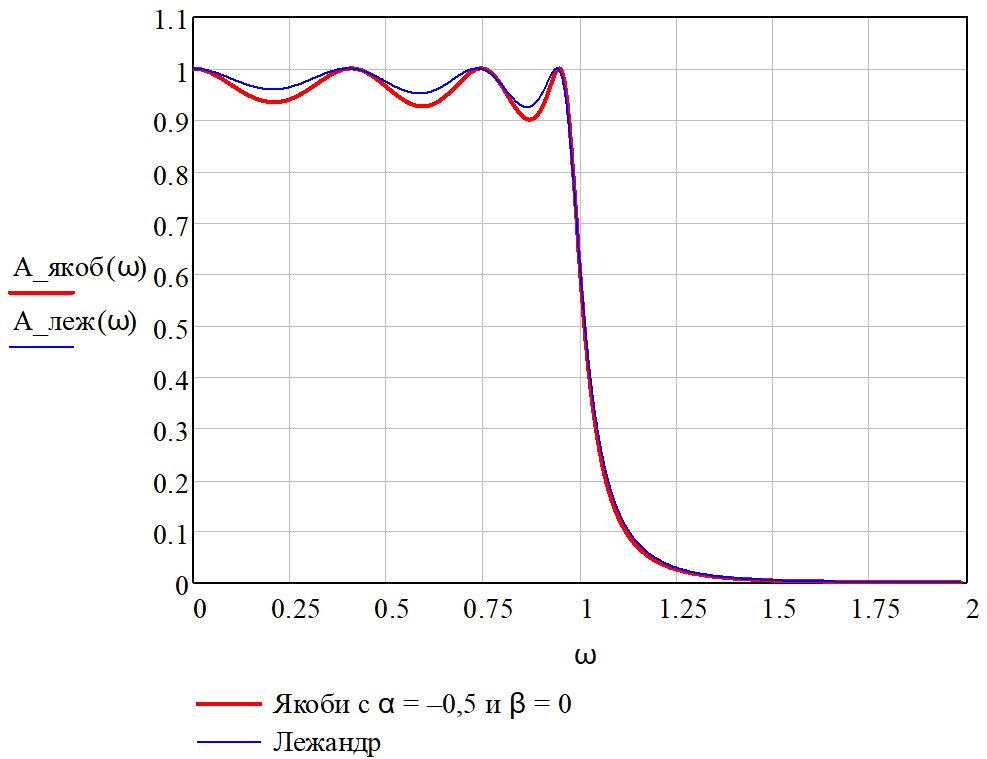
На рис. 15 приведено сравнение амплитудно-частотных характеристик фильтра, аппроксимированных полиномами Лежандра и Якоби с параметрами α = –0,5 и β = 0 при одинаковых заданных требованиях к фильтру. Допустимое отклонение значения АЧХ в полосе пропускания от единицы равно δ₁ = 1 –  ≈ 0,293, допустимое отклонение значения АЧХ от нуля в полосе задерживания равно δ₂ = 0,0005, нормированное значение граничной частоты полосы задерживания равно Ω_k = 2. Соответствующие порядки фильтров равны семи: n_якоб. = n_леж. = 7.

Рис. 15 – Амплитудно-частотные характеристики нормированного фильтра нижних частот, аппроксимированные полиномами Лежандра и Якоби с α = –0,5 и β = 0

 

Как следует из рис. 15, величина пульсаций при использовании полинома Якоби с α = –0,5 и β = 0 превышает величину пульсаций при использовании полинома Лежандра. Порядки фильтров одинаковы, крутизна спада АЧХ одинакова. Следовательно, в данном случае, при таких значениях α и β предпочтение следует отдать полиному Лежандра, однако если параметр β = 0,5, то амплитудно-частотная характеристика принимает вид (рис. 16).

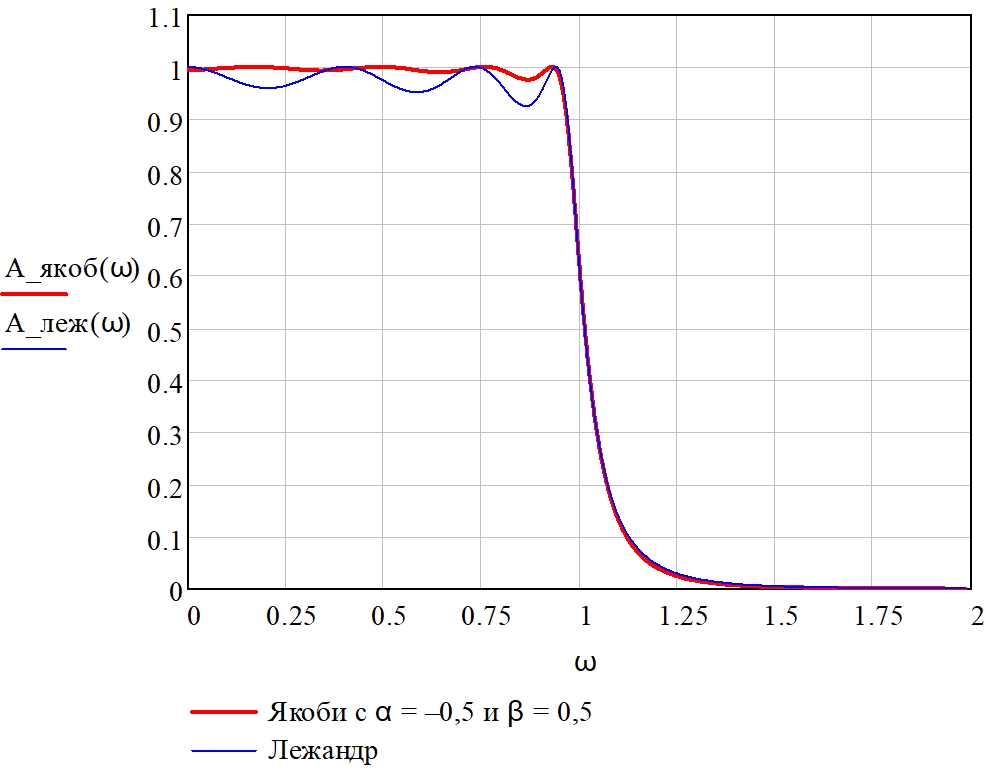
Рис. 16 – Амплитудно-частотные характеристики нормированного фильтра нижних частот, аппроксимированные полиномами Лежандра и Якоби с α = –0,5 и β = 0,5

 

В данном случае полином Якоби с параметрами α = –0,5 и β = 0,5 обеспечивает практически равномерную АЧХ в полосе пропускания по сравнению с использованием полиномов Лежандра. Крутизна спада АЧХ при этом сохраняется практически неизменной. Однако порядок фильтра в этом случае оказывается выше, чем при использовании полинома Лежандра. В данном случае при выбранных α = –0,5 и β = 0,5 предпочтение может быть отдано полиному Якоби, исходя из соображений обеспечения минимальных линейных искажений при передаче сигнала.

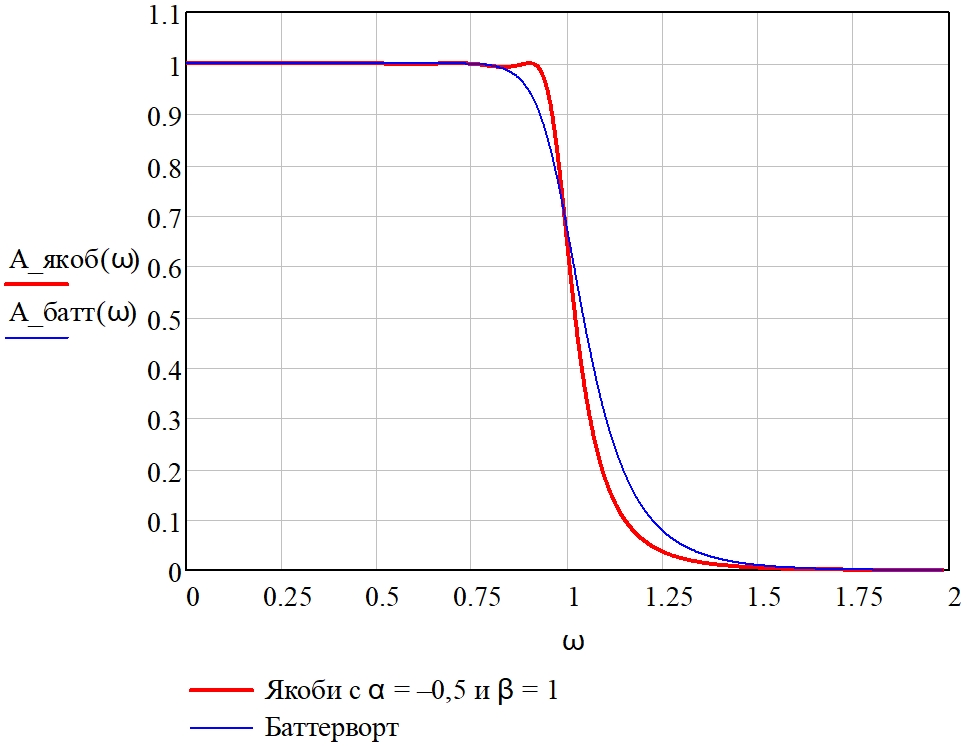
Аналогично проведено сравнение амплитудно-частотных характеристик фильтра, аппроксимированных функциями Баттерворта и полиномами Якоби с параметрами α = –0,5 и β = 1 (рис. 17). При α = –0,5 и β = 1 полином Якоби имеет существенно незначительные пульсации, т. е. АЧХ в полосе пропускания практически совпадает с характеристикой на степенных функциях Баттерворта. При этом порядок фильтра при использовании аппроксимации полиномом Якоби составляет n_якоб. = 8, а при степенной функции Баттерворта – n_батт. = 11, из чего следует, что полином Якоби при порядке n_якоб. = 8 обеспечивает большую крутизну спада АЧХ, чем полином Баттерворта при n_батт. = 11.

Рис. 17 – Амплитудно-частотные характеристики нормированного фильтра нижних частот, аппроксимированные степенными функциями Баттерворта и полиномами Якоби со значениями α = –0,5 и β = 1

  Заключение

Таким образом, из проведённого исследования следует, что аппроксимация на основе полиномов Якоби является наиболее обобщённым вариантом полиномиальной аппроксимации амплитудно-частотной характеристики фильтра (за исключением оптимально монотонной аппроксимации). При различных значениях параметров α и β, удовлетворяющих условию ортогональности полиномов Якоби, можно получать различные по виду АЧХ фильтры n-го порядка, в частности, с повышенной частотной избирательностью, реализованные полиномиальной структурой.

Конфликт интересов	Conflict of Interest
Не указан.	None declared.

Список литературы / References

1. Улахович Д. А. Основы теории линейных электрических цепей / Д. А. Улахович. – СПб.: БХВ-Петербург, 2009. – 816 с.
2. Нестеров С. В. Синтез линейных электрических цепей / С. В. Нестеров. – Волгоград: Изд-во ВолГУ, 2013. – 84 с.
3. Буренко Е. А. Аппроксимация характеристик электрических фильтров рациональными функциями / Е. А. Буренко // XLIV международная молодёжная научная конференция «Гагаринские чтения». Сборник тезисов докладов. Москва, 2018 г. Т.1. С. 375–376.
4. Буренко Е. А. Проектирование активных частотно-избирательных фильтров / Е. А. Буренко, С. В. Нестеров // Труды МАИ. Выпуск №101 от 14.09.2018 г., 26 стр. [Электронный ресурс]. URL: http://trudymai.ru/published.php?ID=97011 (дата обращения: 22.04.2021 г).
5. Butterworth S. On the theory filter amplifier / S. Butterworth. // Experimental Wireless and the Radio Engineer, vol. 7, pp. 536–541, Oct. 1930.
6. Cauer W. Theorie der linearen Wechselstromschaltungen / W. Cauer. Bd. 1, Leipzid: Becker und Erler, 1941; Bd. 2, Berlin: Akademie, 1960.
7. Brafman F. Generating functions and associated Legendre polynomials / F. Brafman. // Quart. J. Math. (Oxford) 10 (2) (1959) 156–160.
8. Chongdar A. K. Group-theoretic study of certain generating functions of Gegenbauer polynomials / A. K. Chongdar // J. Orissa Math. Soc. 2 (1983) 71–85.
9. Gospodarczyk P. Efficient modified Jacobi-Bernstein basis transformation / Gospodarczyk,  Woźny, // arXiv.org, 2017. [Electronic resource]. URL: http://poivs.tsput.ru/Downloads/Publication/1701.03058v1.pdf (accessed: 22.04.2021).
10. Alam S. On Some Mixed Trilateral Generating Functions of Modified Jacobi Polynomials by Group Theoretic Method, Univer / S. Alam and A. K. Chongdar // Jour. Appli. Math. 1(2), 63-71 (2013). [Electronic resource]. URL: http://www.hrpub.org/download/201309/ujam.2013.010205.pdf (accessed: 22.04.2021).

Список литературы на английском языке / References in English

1. Ulakhovich D. A. Osnovy teorii linejjnykh ehlektricheskikh cepejj [Fundamentals of the Theory of Linear Electrical Circuits] / D. A. Ulakhovich. - St. Petersburg: BKhV-Petersburg, 2009. - 816 p. [in Russian]
2. Nesterov S. V. Sintez linejjnykh ehlektricheskikh cepejj [Synthesis of Linear Electrical Circuits] / S. V. Nesterov. - Volgograd: Volgograd State University Publishing house, 2013. - 84 p. [in Russian]
3. Burenko E. A. Approksimacija kharakteristik ehlektricheskikh fil'trov racional'nymi funkcijami. XLIV mezhdunarodnaja molodjozhnaja nauchnaja konferencija «Gagarinskie chtenija». Sbornik tezisov dokladov [Approximation of the Characteristics of Electric Filters by Rational Functions. XLIV International Youth Scientific Conference "Gagarin Readings". A Collection of Abstracts] / E. A. Burenko. Moscow, 2018 Vol. 1, pp. 375-376. [in Russian]
4. Burenko E. A. Proektirovanie aktivnykh chastotno-izbiratel'nykh fil'trov [Design of Active Frequency-Selective Filters] / E. A. Burenko, S. V. Nestervoc. Moscow, "Trudy MAI". Issue No. 101 of 14.09.2018, 26 pages. URL: http://trudymai.ru/published.php?ID=97011 (accessed: 22.04.2021) [in Russian]
5. Butterworth S. On the theory filter amplifier / S. Butterworth. // Experimental Wireless and the Radio Engineer, vol. 7, pp. 536–541, Oct. 1930.
6. Cauer W. Theorie der linearen Wechselstromschaltungen [Theory of linear AC Circuits] / W. Cauer. Bd. 1, Leipzid: Becker und Erler, 1941; Bd. 2, Berlin: Akademie, 1960. [in German]
7. Brafman F. Generating functions and associated Legendre polynomials / F. Brafman. // Quart. J. Math. (Oxford) 10 (2) (1959) 156–160.
8. Chongdar A. K. Group-theoretic study of certain generating functions of Gegenbauer polynomials / A. K. Chongdar // J. Orissa Math. Soc. 2 (1983) 71–85.
9. Gospodarczyk P. Efficient modified Jacobi-Bernstein basis transformation / Gospodarczyk,  Woźny, // arXiv.org, 2017. [Electronic resource]. URL: http://poivs.tsput.ru/Downloads/Publication/1701.03058v1.pdf (accessed: 22.04.2021).
10. Alam S. On Some Mixed Trilateral Generating Functions of Modified Jacobi Polynomials by Group Theoretic Method, Univer / S. Alam and A. K. Chongdar // Jour. Appli. Math. 1(2), 63-71 (2013). [Electronic resource]. URL: http://www.hrpub.org/download/201309/ujam.2013.010205.pdf (accessed: 22.04.2021).