АЛГОРИТМ РАСЧЕТА НЕЧЕТКИХ И ИНТЕРВАЛЬНЫХ ОЦЕНОК ВРЕМЕННЫХ ПАРАМЕТРОВ СЕТЕВОЙ МОДЕЛИ ПРОЕКТА
АЛГОРИТМ РАСЧЕТА НЕЧЕТКИХ И ИНТЕРВАЛЬНЫХ ОЦЕНОК ВРЕМЕННЫХ ПАРАМЕТРОВ СЕТЕВОЙ МОДЕЛИ ПРОЕКТА
Научная статья
Леденев М.Ю.1, Сергиенко М.А.2, *
2 ORCID: 0000-0003-1322-9624;
1, 2 Воронежский государственный университет, Воронеж, Россия
* Корреспондирующий автор (sergienko-m-a[at]yandex.ru)
АннотацияВ статье рассматривается задача календарного планирования работ проекта при условии, что продолжительности работ заданы приближенно в форме нечетких треугольных чисел. Согласно принципу декомпозиции, нечеткое число может быть представлено совокупностью α-срезов, что позволяет использовать интервальную арифметику для организации вычислений. В качестве базового алгоритма для определения временных параметров рассматривается алгоритм для сети, основанный на нахождении максимальных (критических) путей в бесконтурном графе. Предложен алгоритм расчета временных параметров сетевой модели проекта в форме интервальных чисел, которые являются α-срезами соответствующих нечетких чисел. Отличительной особенностью алгоритма является то, что ранние и поздние времена наступления событий содержат в явном виде параметр α. При заданном α формируется конкретное множество ранних и поздних времен наступления событий. Кроме того, зная коэффициенты неопределенности нечетких чисел, можно перейти к представлению временных параметров нечеткими числами. В статье приведены подробные расчеты для иллюстративного примера. Алгоритм позволяет реализовать стратегию «мягкого» планирования проекта.
Ключевые слова: проект, интервальное число, нечеткое число, α-срез.
AN ALGORITHM FOR CALCULATING FUZZY AND INTERVAL ESTIMATIONS OF THE TIME PARAMETERS OF NETWORK MODEL OF A PROJECT
Research article
Ledenev M.Yu.1, Sergienko M.A.2, *
2 ORCID: 0000-0003-1322-9624;
1, 2 Voronezh State University, Voronezh, Russia
* Corresponding author (sergienko-m-a[at]yandex.ru)
AbstractThe article deals with the problem of calendar planning of project activities, provided that the duration of work is given approximately in the form of fuzzy triangular numbers. According to the decomposition principle, a fuzzy number can be represented by a set of α-slices, which allows for using interval arithmetic for organizing calculations. As a basic algorithm for determining the time parameters, the authors consider an algorithm for a network based on finding the maximum (critical) paths in an acyclic graph. The study proposes an algorithm for calculating the time parameters of the network model of the project in the form of interval numbers, which are α-slices of the corresponding fuzzy numbers. A distinctive feature of the algorithm is that the early and late times of the occurrence of events explicitly contain the α parameter. For a given α, a specific set of early and late event occurrence times is formed. In addition, knowing the uncertainty coefficients of fuzzy numbers, one can proceed to the representation of time parameters by fuzzy numbers. The article provides detailed calculations for an illustrative example. The algorithm allows for implementing a strategy of "soft" project planning.
Keywords: project, interval number, fuzzy number, α-slice.
ВведениеПовышение сложности современных проектов обусловливает развитие эффективных методов планирования, обеспечивающих оптимизацию всего процесса реализации проекта. По оценкам исследователей [1]: только 44% проектов обычно завершаются вовремя; в среднем проекты занимают 222% от начальной запланированной продолжительности, 70% проектов сокращают исходный объем работ; 30% проектов закрываются досрочно. Развитие теории управления сложными комплексами работ является актуальным направлением исследований. К основным методам сетевого планирования относят следующие: МКП - метод критического пути с детерминированной технологией сетевого планирования [2]; PERT (Program Evaluation and Review Technique) – технология оценки планов реализации проекта с учетом случайного времени выполнения операций [2]; GERT (Graphical Evaluation and Review Technique) – стохастическая сетевая технология, обобщающая классический сетевой график [3]. Для небольших по объему проектов еще до появления методов сетевого планирования использовалась ленточная диаграмма Гантта, которая позволяет оценить текущее состояние проекта и загруженность исполнителей. Существующий на данный момент инструментарий управления проектами в форме программных систем и сред (например, Open Plan, Primavera Project Planner, Microsoft Project, Spider Project и др.) позволяет руководителю эффективно управлять процессом реализации работ, а также маневрировать ресурсами в условиях полной информированности о продолжительности работ. Однако в реальной ситуации продолжительность работ может быть задана только приближенно на основе накопленного опыта или экспертных оценок. Наличие фактора неопределенности обусловливает развитие подходов к решению задач планирования работ проекта с учетом приближенных моделей обработки информации. Метод PERT работает в предположении, что продолжительность работы является случайной величиной, и позволяет определить вероятность того, что проект будет реализован в течение заданного времени. В [4] представлен метод нахождения нечеткого критического пути. В [5,6] предложены подходы для календарного планирования работ проекта на основе гауссовых нечетких чисел, однако сложность вычислений препятствует их широкому практическому использованию.
Цель статьи заключается в представлении алгоритма планирования, ориентированного на представление продолжительности работ проекта в форме треугольных нечетких чисел. Особенностью подхода является то, что нечеткое число представляется в виде совокупности α-срезов, что позволяет использовать для вычислений интервальную арифметику.
- Математическая модель проекта
Под проектом понимается комплекс работ, которые выполняются в определенной последовательности и требуют для своего выполнения времени и ресурсного обеспечения [1].
На этапе структурного моделирования, с одной стороны, проект разбивается на совокупность работ (операций), для каждой из которых осуществляется оценка необходимого для ее выполнения времени, с другой стороны, устанавливается логическая последовательность работ и формируется математическая модель в форме ориентированного графа [7].
На этапе календарного планирования определяются моменты начала и окончания каждой работы, и выявляются те из них (критические), которые потребуют пристального внимания при реализации проекта для его успешного окончания в директивный срок. Выявление некритических работ необходимо для нахождения резервов времени проекта.
Введем основные понятия сетевого моделирования, базируясь на [7], [8].
Сеть – это бесконтурный взвешенный ориентированный граф, в котором имеется одна вершина, имеющая только выходящие дуги, и одна вершина, имеющая только входящие дуги. Сеть также называется сетевым графиком.
В сетевом графике каждой дуге соответствует работа, продолжительность которой определяет вес дуги. Каждая вершина есть событие, которое заключается в том, что работы, соответствующие входящим дугам, завершены, а работы, соответствующие выходящим дугам, готовы к выполнению.
Вершина без входящих дуг называется исходным событием, а без выходящих – завершающим событием сети.
Каждому событию i можно поставить в соответствие следующие параметры [8]: ![]() - раннее время наступления i-го события - время, раньше которого событие i наступить не может, иначе не будут завершены работы, которые ему предшествуют;
- раннее время наступления i-го события - время, раньше которого событие i наступить не может, иначе не будут завершены работы, которые ему предшествуют; ![]() - позднее время наступления i-го события - время, позже которого событие i наступить не должно, иначе увеличится время, необходимое для реализации проекта.
- позднее время наступления i-го события - время, позже которого событие i наступить не должно, иначе увеличится время, необходимое для реализации проекта.
Заметим, что ![]() , при этом величина
, при этом величина ![]() называется резервом времени i-го события.
называется резервом времени i-го события.
Зафиксируем событие i. Очевидно, что для его наступления необходимо, чтобы все работы, которые ему предшествуют, были завершены. Тогда раннее время ![]() можно интерпретировать как длину максимального пути из исходного события в данное событие i.
можно интерпретировать как длину максимального пути из исходного события в данное событие i.
Длина максимального пути из исходного события в завершающее – это время, необходимое для реализации всего проекта, так как время завершения всего комплекса работ не может быть меньше, чем суммарная продолжительность всех работ вдоль самого длинного пути. Это время называется критическим и обозначается ![]() . Сетевой график может иметь несколько критических путей. Все они имеют одинаковую длину
. Сетевой график может иметь несколько критических путей. Все они имеют одинаковую длину ![]() .
.
Позднее время ![]() наступления i-го события можно интерпретировать как разность между длиной критического пути и длиной критического пути из i-го события в завершающее событие сети. Работы и события, принадлежащие критическому пути, также называются критическими. Особенность критических работ заключается в том, что они не имеют резервов времени, поэтому невыполнение срока окончания любой из критических работ приводит к увеличению критического времени
наступления i-го события можно интерпретировать как разность между длиной критического пути и длиной критического пути из i-го события в завершающее событие сети. Работы и события, принадлежащие критическому пути, также называются критическими. Особенность критических работ заключается в том, что они не имеют резервов времени, поэтому невыполнение срока окончания любой из критических работ приводит к увеличению критического времени ![]() .
.
Имеет место следующее утверждение [2]: для того, чтобы событие i принадлежало критическому пути необходимо и достаточно, чтобы раннее и позднее времена наступления этого события совпадали, то есть ![]() .
.
К временным параметрам сетевого графика также относятся резервы времени работ [8].
- Алгоритм определения временных параметров проекта
Шаг 1. Топологическая сортировка сети.
Получить правильную нумерацию вершин сетевого графика, при этом исходное событие сети получает номер 0, а завершающее - номер n.
Шаг 2. Определение ранних времен наступления событий.
Положить ![]() . Двигаясь по пронумерованной сети в порядке возрастания вершин, для каждой вершины j определить
. Двигаясь по пронумерованной сети в порядке возрастания вершин, для каждой вершины j определить
![]()
где ![]() - множество вершин, из которых дуги ведут в j.
- множество вершин, из которых дуги ведут в j.
Шаг 3. Определение критического пути.
Положить ![]() , где n - завершающее событие сети. Для определения критического пути выполнить следующие действия: из всех дуг, входящих в завершающее событие n, выделить те дуги
, где n - завершающее событие сети. Для определения критического пути выполнить следующие действия: из всех дуг, входящих в завершающее событие n, выделить те дуги ![]() , которые удовлетворяют условию
, которые удовлетворяют условию ![]() . Затем рассматриваются те вершины, из которых выходят выделенные дуги, и снова из входящих в них дуг выделяются те, которые удовлетворяют тому же условию. Процесс продолжается до тех пор, пока не будет достигнуто исходное событие сети. Путь из исходного события в завершающее событие, составленный из выделенных дуг, является критическим.
. Затем рассматриваются те вершины, из которых выходят выделенные дуги, и снова из входящих в них дуг выделяются те, которые удовлетворяют тому же условию. Процесс продолжается до тех пор, пока не будет достигнуто исходное событие сети. Путь из исходного события в завершающее событие, составленный из выделенных дуг, является критическим.
Шаг 4. Определение поздних времен наступления событий.
Положить ![]() . Двигаясь по сети от завершающего события в порядке убывания номеров вершин, определить для каждого i-го события
. Двигаясь по сети от завершающего события в порядке убывания номеров вершин, определить для каждого i-го события
![]()
где ![]() - множество вершин, в которые ведут дуги из i.
- множество вершин, в которые ведут дуги из i.
К наиболее распространенным формам представления приближенной информации относятся интервальные и нечеткие числа [9].
Под интервальным числом подразумевается любой промежуток ![]() c включенными или исключенными границами, так что интервалы, полуинтервалы и отрезки, по сути, являются интервальными числами.
c включенными или исключенными границами, так что интервалы, полуинтервалы и отрезки, по сути, являются интервальными числами.
Пусть ![]() - интервальные числа, тогда определим арифметические операции над ними следующим образом [10]:
- интервальные числа, тогда определим арифметические операции над ними следующим образом [10]:
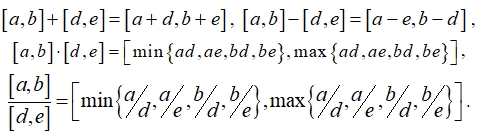
Будем считать, что 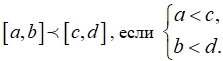
Являясь одним из основных понятий нечеткой математики, нечеткие числа используются для формализации приближенной информации вида «x приблизительно равно a». Нечеткое число A – это число с плохо определенными границами, поэтому для его задания необходимо задать параметр a (модальное значение) и поведение на границах. Будем рассматривать нечеткие треугольные числа с функцией принадлежности вида
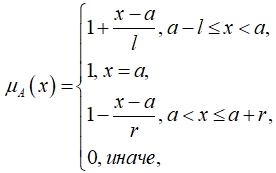
где l, r - соответственно левый и правый коэффициенты неопределенности.
Заметим, что нечеткое треугольное число является нечетким подмножеством числовой прямой и однозначно задается набором параметров ![]() , поэтому его часто обозначают тройкой (
, поэтому его часто обозначают тройкой (![]() ).
).
Для произвольного нечеткого множества A c функцией принадлежности ![]() a-срезом называется обычное множество
a-срезом называется обычное множество
В соответствии с теоремой декомпозиции [8], каждое нечеткое множество можно представить совокупностью a-срезов.
α-Срез треугольного нечеткого числа ![]() представляет собой промежуток
представляет собой промежуток ![]() - это корень уравнения
- это корень уравнения ![]() - корень уравнения
- корень уравнения ![]() . Вычисляя корни, получим
. Вычисляя корни, получим ![]() .
.
Перебирая последовательные значения ![]() с определенным шагом, нечеткое число A можно представить множеством
с определенным шагом, нечеткое число A можно представить множеством
![]()
Заметим, что при ![]() получим самый «широкий» интервал
получим самый «широкий» интервал ![]() ; при возрастании a от 0 до 1 интервал сужается, и при
; при возрастании a от 0 до 1 интервал сужается, и при ![]() превращается в точку.
превращается в точку.
Имеет место следующее утверждение: пусть A и B - нечеткие числа, α-срезы которых есть ![]() . Если
. Если ![]() , то при любом
, то при любом ![]() имеем
имеем ![]() .
.
Заметим, что 
Один из подходов к определению нечетких операций базируется на интервальной арифметике [10]. Пусть A и B - нечеткие числа, ![]() - их a-срезы, - символ арифметической операции, тогда для любых
- их a-срезы, - символ арифметической операции, тогда для любых ![]() имеет место следующее определение:
имеет место следующее определение:
где ![]() .
.
Таким образом, арифметические операции над нечеткими числами сводятся к арифметическим операциям над соответствующими a-срезами.
3.2 Алгоритм расчета временных параметров проекта на основе продолжительностей работ, заданных интервальными числами
Пусть продолжительности работ заданы в форме треугольных нечетких чисел ![]() . Зафиксируем
. Зафиксируем ![]() и перейдем к α-срезам
и перейдем к α-срезам ![]() . Также введем интервальные числа
. Также введем интервальные числа
определяющие α-срезы следующих параметров: ![]() - раннее время наступления i-го события и
- раннее время наступления i-го события и ![]() - позднее время наступления i-го события. Поскольку классический алгоритм расчета временных параметров использует нулевые метки, то введем интервальное число
- позднее время наступления i-го события. Поскольку классический алгоритм расчета временных параметров использует нулевые метки, то введем интервальное число
Изложим модифицированный алгоритм.
Шаг 1 (упорядочивание событий). Данный шаг не учитывает форму представления информации, поэтому он реализуется так же, как в классическом случае, т.е. выполняется топологическая сортировка, в результате которой вершинам приписываются «правильные» номера, упорядочивающие события сетевого графика, при этом исходное событие сети получает номер 0, а завершающее - номер n.
Шаг 2 (определение ранних времен наступления событий). Зафиксировать ![]() . Положить
. Положить ![]() . Рассматривая вершины-события в порядке возрастания их номеров, для каждого события j определить раннее время наступления по формуле
. Рассматривая вершины-события в порядке возрастания их номеров, для каждого события j определить раннее время наступления по формуле
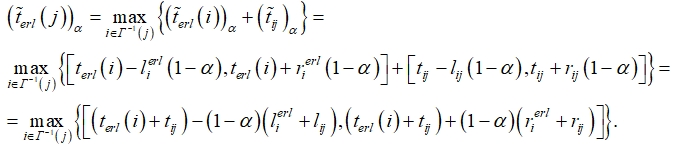
где ![]() - множество вершин, из которых дуги ведут в j.
- множество вершин, из которых дуги ведут в j.
Шаг 3 (определение критического пути). Положить
![]()
где n - завершающее событие сети. Для определения критического пути выполнить следующие действия: положить ![]() , и выделить те дуги
, и выделить те дуги ![]() , которые удовлетворяют условию
, которые удовлетворяют условию
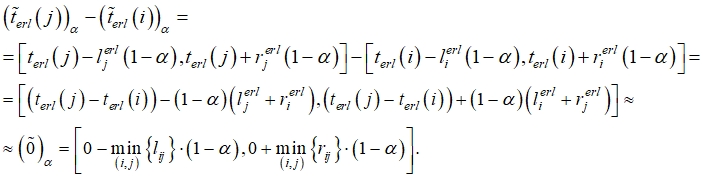
Затем рассматриваются те вершины, из которых выходят выделенные дуги, и снова из входящих в них дуг выделяются те, которые удовлетворяют тому же условию. Процесс продолжается до тех пор, пока не будет достигнуто исходное событие сети. Путь из исходного события в завершающее событие, составленный из выделенных дуг, является критическим.
Шаг 4 (определение поздних времен).
Положить ![]() . Двигаясь по сети в порядке убывания правильных номеров вершин, определить
. Двигаясь по сети в порядке убывания правильных номеров вершин, определить
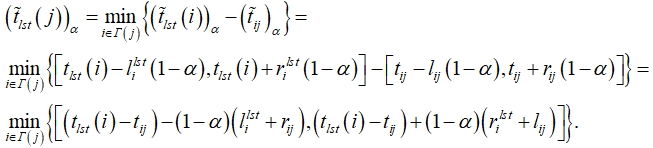
Для контроля вычислений будем использовать условие
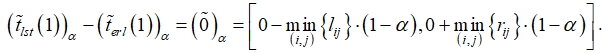
Нечеткая информация относительно продолжительности операций может быть получена от экспертов в ситуации, когда проект и каждая операция являются уникальными и отсутствуют как нормативы, так и статистические данные. Тестирование изложенного алгоритма показало, что, если продолжительности работ заданы интервальными числами с малой шириной, то получаются приемлемые результаты, причем возможна их эффективная оптимизация за счет сдвигов. Если среди продолжительностей имеются интервалы с большой шириной, то это влияет на критическое время – оно задается «широким» интервальным числом, и прогнозировать время, необходимое для выполнения проекта становится невозможно.
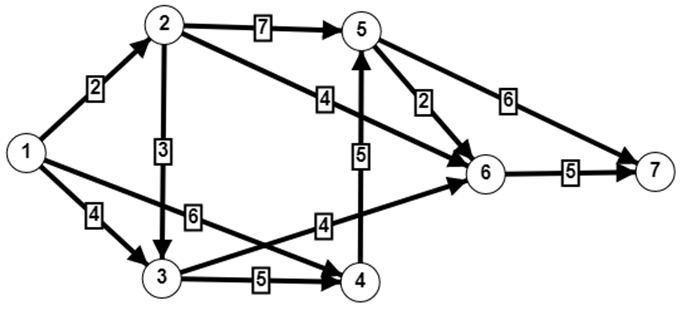
3.3 Иллюстративный пример Рассмотрим сетевой график, представленный на рис. 1, и рассчитаем его временные параметры.Рис. 1 – Пример сетевого графика
По формулам найдем ранние времена наступления событий: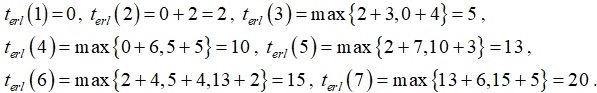 Таким образом,
Таким образом, 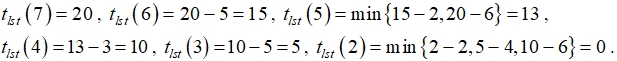 Теперь рассмотрим ситуацию, когда продолжительности работ заданы приближенно в форме нечетких чисел (табл. 1).
Теперь рассмотрим ситуацию, когда продолжительности работ заданы приближенно в форме нечетких чисел (табл. 1).
Таблица 1 – Продолжительности работ в форме нечетких чисел
| |
(1,2) | (1,3) | (1,4) | (2,3) | (2,5) | (2,6) | (3,4) | (3,6) | (4,5) | (5,6) | (5,7) | (6,7) |
| |
2 | 4 | 6 | 3 | 7 | 4 | 5 | 4 | 5 | 2 | 6 | 5 |
| 1 | 1 | 0.5 | 2 | 1 | 1 | 0.5 | 2 | 1 | 1 | 2 | 0.5 | |
| |
0.5 | 2 | 0.5 | 1 | 1 | 2 | 0.5 | 0.5 | 1 | 1 | 1 | 2 |
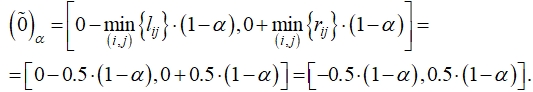
При определении критического времени целесообразно перейти к α-срезу вида ![]() , поскольку в этом случае нечеткий нуль считается точкой отсчета, началом реализации проекта.
, поскольку в этом случае нечеткий нуль считается точкой отсчета, началом реализации проекта.
На основе предложенного алгоритма найдем ранние времена наступления событий для сетевого графика на рис. 1.
![]()
где ![]()
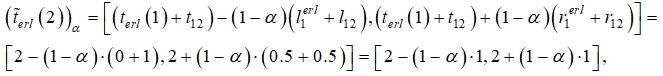
где ![]()
так как данный интервал находится правее, причем при возрастании a положение интервалов относительно друг друга не изменится. Таким образом,
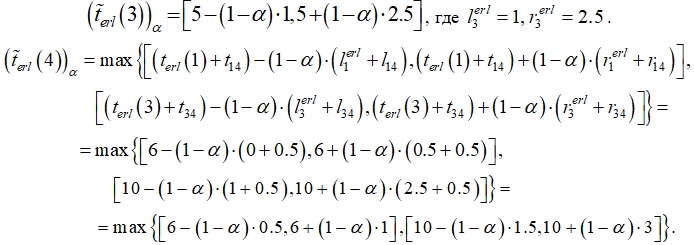 При
При 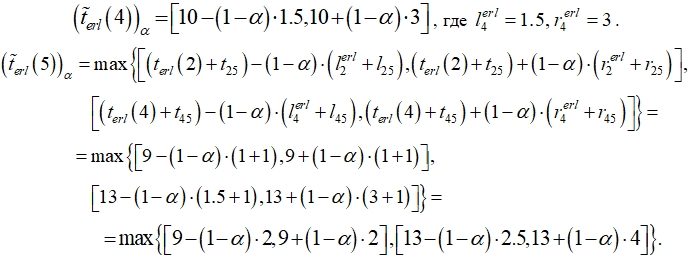 Сравнивая самые «широкие» интервалы при
Сравнивая самые «широкие» интервалы при 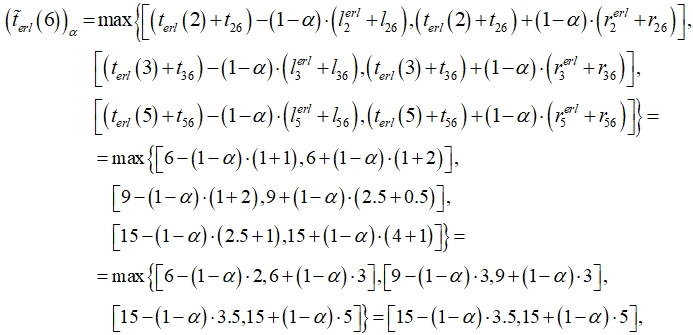 что следует из аналогичных рассуждений при
что следует из аналогичных рассуждений при 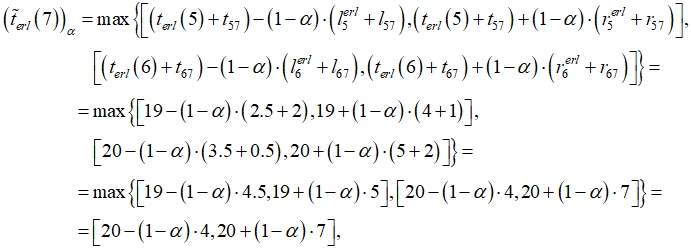
так как при ![]() второй интервал находится правее первого, здесь
второй интервал находится правее первого, здесь ![]() .
.
Найденные ранние времена задаются интервальными числами, левые и правые границы которых зависят от параметра ![]() , при этом чем ближе a к 1, тем меньше уровень неопределенности; при
, при этом чем ближе a к 1, тем меньше уровень неопределенности; при ![]() результаты расчетов совпадают с классическим случаем.
результаты расчетов совпадают с классическим случаем.
Выберем ![]() , тогда ранние времена наступления событий определяются следующими интервальными числами:
, тогда ранние времена наступления событий определяются следующими интервальными числами:
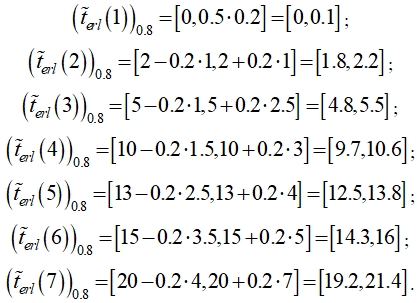
Использование интервальной информации позволяет осуществить «мягкое» планирование работ проекта и оценить возможные отклонения. В приведенном примере критическое время определяется ранним временем завершающего события и равно ![]() . Заметим, что найденные интервальные числа, определяющие ранние времена наступления событий и критическое время, включают точные значения, полученные классическим алгоритмом, причем ширина интервалов вполне согласуется с приближенными исходными данными. Аналогичным образом определяются поздние времена наступления событий. Зная коэффициенты неопределенности, которые легко вычисляются для каждой оценки, можно перейти к представлению параметров нечеткими числами.
. Заметим, что найденные интервальные числа, определяющие ранние времена наступления событий и критическое время, включают точные значения, полученные классическим алгоритмом, причем ширина интервалов вполне согласуется с приближенными исходными данными. Аналогичным образом определяются поздние времена наступления событий. Зная коэффициенты неопределенности, которые легко вычисляются для каждой оценки, можно перейти к представлению параметров нечеткими числами.
3.4 Практическое использование предложенного алгоритма
Для крупных организаций, обладающих значительными ресурсами, при управлении проектами целесообразно использовать существующие программные решения, но небольшие компании зачастую не могут себе позволить дорогостоящее программное обеспечение, которое к тому же имеет избыточный функционал. Однако имея в своем портфеле даже несколько проектов, принятых к реализации, они сталкиваются с проблемой эффективного управления выполнением каждого из проектов и всей совокупности проектов с учетом имеющихся ресурсов и ограниченного времени. Для решения возникающих задач предложена система управления проектами в форме программной среды, в которой собраны инструменты выработки и реализации сбалансированных управленческих решений, охватывающих разные уровни и стадии управления проектами в данной организации. Особенностью системы является ее открытость и модульность, что позволяет дополнять программную среду новыми инструментами. В качестве базовых инструментов выбраны следующие: формирование мультипроектов и согласованное управление их реализацией; инструменты временного анализа проектов; разработка механизмов распределения ресурсов между проектами (между работами проекта) и их оптимизация на основе общего пула ресурсов; формирование команды проекта и механизмов стимулирования ее участников. Инструменты временного анализа проектов включают алгоритмы расчета временных параметров сетевого графика с учетом способа задания продолжительности выполнения работ проекта в том числе, если информация задается приближенно только для некоторых работ. Выбирая алгоритм и определяя параметры настройки, пользователь может сам сконструировать алгоритм расчета временных параметров проекта. Предложенный в данной статье алгоритм включен в комплекс алгоритмов для решения задачи календарного планирования, из которого пользователь осуществляет свой выбор. Его преимуществом является возможность оперативной корректировки плана на основе «сдвигов» работ в рамках найденных интервалов.
Рассмотрим пример. Торгово-развлекательные центры (ТРЦ) – относительно новый для нашей страны формат, дающий возможность приобрести товары различных категорий в одном месте, чередуя шопинг с развлечениями и посещениями кафе. Основная задача владельца ТРЦ - сдать объект в эксплуатацию и привлечь арендаторов, после чего центр начнет приносить доход без существенных затрат. Для строительства ТРЦ необходимо особенно тщательно провести расчеты, составить проект и сметную документацию, поскольку стартовые вложения очень велики. В табл. 2 представлены работы по строительству и вводу в эксплуатацию ТРЦ «Рябина», продолжительности работ заданы в форме нечетких чисел. На рис. 2 изображен сетевой график проекта, построенный по табл. 2.
Таблица 2 - Перечень работ и их продолжительностей
| Работа | Содержание | Продолжительность, нед. | Предшествующие работы |
| A | Анализ рынка недвижимости города | (2,1,1) | - |
| B | Выбор земельного участка | (6,1.3,1) | A |
| C | Разработка концепции торгового центра | (4,1,0.2) | B |
| D | Заключение инвестиционного договора | (4,1,0.7) | C |
| E | Получение кредита | (8,1,1) | D |
| F | Внесение в госреестр, постановка на учет в налоговых и административных органах | (4,1,0.3) | E |
| G | Предброкеридж и внесение изменений в концепцию | (5,1,0.5) | C |
| H | Разработка рабочей проектной документации | (4,0.5,0.5) | F |
| I | Заказ и покупка оборудования | (6,0.4,0.8) | G |
| J | Подготовка стройплощадки и закладка фундамента | (6,1.3,0.5) | H |
| K | Монтаж вертикальных стен, перекрытий и крыши | (8,1,1.2) | J |
| L | Монтаж наружных сетей | (7,0.5,1) | J |
| M | Монтаж систем отопления, вентиляции и кондиционирования | (8,1,1.2) | L |
| N | Электромонтажные работы | (4,0.5,0.5) | L |
| O | Отделочные работы и дизайн интерьера | (9,1,1) | M, N |
| P | Установка оборудования | (3,0.6,0.4) | O |
| Q | Наем и обучение персонала | (8,0.5,1) | O |
| R | Брокеридж торгового центра | (2,0.4,0.4) | P |
| S | Проведение маркетинговой компании | (2,1,0.5) | O, P |
| T | Подготовка к церемонии открытия | (1,0.5,0.5) | Q, R |
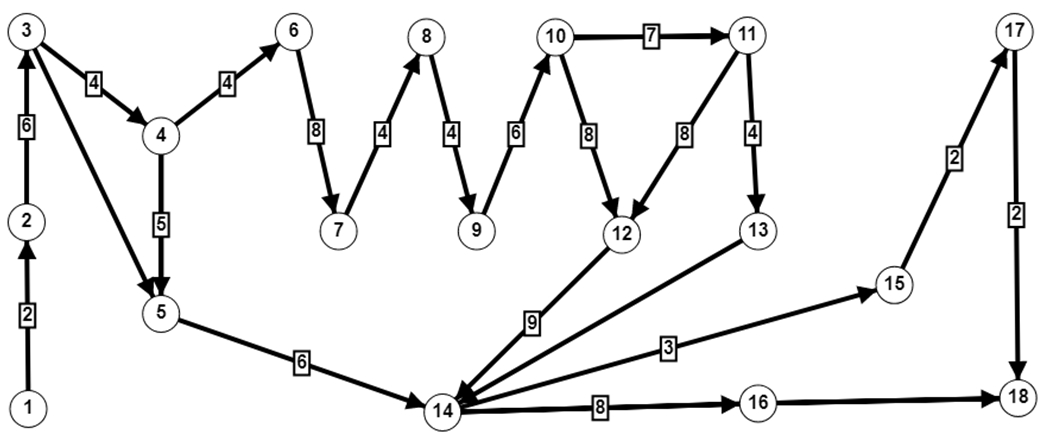
Рис. 2 – Сетевой график проекта
Таблица 3 - Соответствие между дугами и работами в сетевом графике
| A | (1,2) | E | (6,7) | I | (5,14) | M | (11,12) | Q | (14,16) |
| B | (2,3) | F | (7,8) | J | (9,10) | N | (11,13) | R | (15,17) |
| C | (3,4) | G | (4,5) | K | (10,12) | O | (12,14) | S | (17,18) |
| D | (4,6) | H | (8,9) | L | (10,11) | P | (14,15) | T | (16,18) |
С использованием предложенного алгоритма найдены ранние и поздние времена наступления событий, при найдено критическое время реализации проекта в форме интервального [68.4, 71,5]. Критический путь 1-2-3-4-6-7-8-9-10-11-13-14-16-18 определялся на основе модальных значений нечетких чисел. Оказалось, что большинство работ критические, а план является напряженным. Было принято решение об изменении продолжительности некоторых работ на основе перераспределения ресурсов.
Заключение
Сложность современных проектов в различных сферах обусловливает использование моделей приближенной информации при определении временных параметров сетевой модели проекта. Развитый аппарат интервальной арифметики позволяет достаточно просто реализовать операции над нечеткими числами, используя их α-срезы. В статье предложен алгоритм расчета временных параметров сетевого графика в форме их α-срезов. При подстановке конкретного значения α формируется конкретное множество ранних и поздних времен наступления событий. Программная реализация расчетных формул позволит осуществить экспериментальную настройку параметра для конкретного проекта.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Кудрявцев Е. М. Методы сетевого планирования и управления проектом / Е. М. Кудрявцев. – Москва : ДМК Пресс, 2005. – 240 с.
- Таха Х. А. Введение в исследование операций / Х. А. Таха. - Москва : Издательский Дом Вильямс, 2005. - 912 с.
- Филлипс Д. Методы анализа сетей / Д. Филлипс, А. Гарсиа-Диас. – М. : Мир, 1984. – 496 с.
- Балашов В.Г. Метод нечеткого критического пути / В. Г. Балашов, А.Ю.Заложнев // Управление большими системами. – Москва : ИПУ РАН, 2003. – Т. 3. – С. 5-10.
- Леденева Т. М. Нечеткая модель проекта с продолжительностями работ в форме обобщенных гауссовых чисел / Т. М. Леденева, Д. А. Черменев // Вестник ВГУ. Серия: Системный анализ и информационные технологии, 2015. - № 2. - С. 72-81.
- Шашкин А.И. Календарное планирование работ по проекту на основе нечетких исходных данных / А.И. Шашкин, М.М. Ширяев // Вестник СамГУ. Естественнонаучная серия. – Самара, 2008. – №3 (62). – С. 208-216.
- Бурков В.Н. Теория графов в управлении организационными системами / В.Н. Бурков, А.Ю. Заложнев, Д.А. Новиков. – М. : СИНТЕГ, 2001. – 124 с.
- Леденева Т. М. Специальные главы математики. Прикладные дискретные модели / Т. М. Леденева. Воронеж : Издательство ВГТУ, 2000. - 134 с.
- Леденева Т. М. Обработка нечеткой информации / Т. М. Леденева. – Воронеж: ВГУ, 2006. – 233 с.
- ПегатА. Нечеткое моделирование и управление / А.Пегат. – М.: БИНОМ, 2009. – 798 с.
Список литературы на английском языке / References in English
- Kudryavtsev E.M. Metody setevogo planirovanija i upravlenija proektom [Methods of network planning and project management] / E.M. Kudryavtsev. Moscow: DMK Press; 2005. 240 p. [in Russian]
- Taha Kh. A. Vvedenie v issledovanie operacij [Introduction to operations research] / Kh. A. Taha.. Moscow: Williams Publishing House; 2005. 912 p. [in Russian]
- Phillips D. Metody analiza setej [Methods of network analysis] / D. Phillips, A. Garcia-Diaz. Moscow: Mir; 1984. 496 p. [in Russian]
- Balashov V.G. Metod nechetkogo kriticheskogo puti [Fuzzy critical path method] / V.G. Balashov, A.Yu. Zalozhnev // Upravlenie bol'shimi sistemami [Management of large systems]. Moscow: Institute of Control Sciences of Russian Academy of Sciences; 2003. Vol. 3. Pp. 5-10. [in Russian]
- Ledeneva T.M. Nechetkaja model' proekta s prodolzhitel'nostjami rabot v forme obobshhennyh gaussovyh chisel [Fuzzy model of the project with duration of work in the form of generalised Gaussian numbers] / T.M. Ledeneva, D.A. Chermenev // Vestnik VGU. Serija: Sistemnyj analiz i informacionnye tehnologii [Bulletin of Voronezh State University. Series: System analysis and information technology]; 2015. No. 2. Pp. 72-81. [in Russian]
- Shashkin A.I. Kalendarnoe planirovanie rabot po proektu na osnove nechetkih ishodnyh dannyh [Scheduling of work on the project based on fuzzy initial data] / A.I. Shashkin, M.M. Shiryaev // Vestnik SamGU. Estestvennonauchnaja serija [Bulletin of Samara State University. Natural science series]; Samara. 2008. No. 3 (62). Pp. 208-216. [in Russian]
- Burkov V.N. Teorija grafov v upravlenii organizacionnymi sistemami [Graph theory in the management of organisational systems] / V.N. Burkov, A. Yu. Zalozhnev, D.A. Novikov. Moscow: SINTEG; 2001. 124 p. [in Russian]
- Ledeneva T.M. Special'nye glavy matematiki. Prikladnye diskretnye modeli [Specific chapters of mathematics. Applied discrete models] / T.M. Ledeneva. Voronezh: Voronezh State Technical University Publishing House; 2000. 134 p. [in Russian]
- Ledeneva T.M. Obrabotka nechetkoj informacii [Processing of fuzzy information] / T.M. Ledeneva. Voronezh: Voronezh State University; 2006. 233 p. [in Russian]
- Pegat A. Nechetkoe modelirovanie i upravlenie [Fuzzy modelling and control] / A. Pegat. Moscow: BINOM; 2009. 798 p. [in Russian]