ПРИБЛИЖЕНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ СОСТАВНЫМИ ДВУХТОЧЕЧНЫМИ МНОГОЧЛЕНАМИ ЭРМИТА
ПРИБЛИЖЕНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ СОСТАВНЫМИ ДВУХТОЧЕЧНЫМИ МНОГОЧЛЕНАМИ ЭРМИТА
Научная статья
ФГУП Государственный научно-исследовательский институт авиационных систем, Москва, Россия
* Корреспондирующий автор (vshustov[at]gosniias.ru)
АннотацияРассмотрена задача приближения периодических функций составными двухточечными многочленами Эрмита. Получены конечные формулы представления этих многочленов, которые используют значения функции и ее производных в заданной точке. Указана связь двухточечных многочленов Эрмита и многочлена Тейлора применительно к представлению периодической функции. Приведена оценка приближения, выраженная через оценку производной соответствующего порядка. Указан достаточный признак сходимости последовательности составных двухточечных многочленов к периодической функции. Даны примеры разложения периодических функций с данными о погрешности и ее оценке.
Ключевые слова: периодические функции, двухточечный многочлен Эрмита, оценка погрешности приближения, сходимость последовательности двухточечных многочленов.
APPROXIMATION OF PERIODIC FUNCTIONS BY COMPOSITE TWO-POINT HERMITE POLYNOMIALS
Research article
Shustov V.V. *
ORCID: 0000-0002-2465-7475,
State Research Institute of Aviation Systems, Moscow, Russia
* Corresponding author (vshustov[at]gosniias.ru)
AbstractThis paper deals with polynomial approximating a periodic functions by composite two-point Hermite polynomials. The final formulas of these polynomials, using the function values and its derivatives at a given point, are constructed. The relation of Taylor's polynomial and two-point polynomials with respect to representation of periodic function is specified. The estimation of proximity, expressed through the evaluation of the derivative of the corresponding order is given. A sufficient condition for the convergence of a sequence of two-point polynomials to a given periodic function is established. Examples are given in which periodic function is approximated by a sequence of two-point Hermite polynomials with data on an errors and its evaluation.
Keywords: periodic functions, two-point Hermite polynomial, approximation error estimate, convergence of two-point polynomials sequence.
ВведениеПериодическими функциями называются функции, которые удовлетворяют условию f(x)=f(x+T), где период T > 0 [1, C. 9].
Для представления этих функции используются ряды Фурье. Теория этих рядов представлена в различных источниках, начиная от учебников курса математического анализа и теории функций [2], [3, C. 343], [4] и включая работы, в которых освещаются теоретические и практические аспекты использования этих рядов в курсе численных методов [5, C. 390], [6, C. 282], [7, C. 218].
В рядах Фурье применяются тригонометрические функции f(x) = sin x и f(x) = cos x. Для использования этих функций их необходимо вычислить, применяя многочлены Тейлора.
В настоящей работе предлагается использование составных многочленов для представления периодических функций.
Основные идеи и положения статьи анонсированы в докладе автора [14].
- Постановка и решение задачи
Пусть периодическая функция f(x), которая имеет период T, т.е.
| f(x) = f(x+T), | (1) |
задана на интервале (-∞<x<∞) и имеет производные на этом промежутке.
Пусть также в некоторой точке x0 интервала (-∞,∞) заданы значения функции f(x), а также, ее производных до порядка m включительно:
![]() (2)
(2)
Требуется построить составной многочлен H(x), который определен на заданном интервале (-∞<x<∞). Многочлен H(x) должен удовлетворять также условиям (1) и (2).
Пусть ξ - новая переменная, связанная с переменной x формулой:в которой функция ![]() обозначает дробную часть своего аргумента, т.е
обозначает дробную часть своего аргумента, т.е ![]() . Диапазон изменения переменной ξ , таким образом, определен соотношением:
. Диапазон изменения переменной ξ , таким образом, определен соотношением:
Так как заданная функция периодическая и для нее по условию (2) существуют производные до порядка m включительно, то эти производные должны быть периодическими функциями.
Запишем условия периодичности производных в виде соотношений:
Задача аппроксимации периодической функции на бесконечном интервале преобразована в задачу приближения этой функции на отрезке [0,1] с условиями (2) и (5) на ее производные.
В качестве аппроксимирующей функции будем использовать двухточечный многочлен Эрмита, рассмотренный в [10] и [11] .
Такой приближающий многочлен Hm(ξ(x)), удовлетворяющий условиям (2) и (5), с использованием переменной ξ, определенной формулой (3), можно представить в виде [10, C. 1097]:
где коэффициент ![]() выражается через биномиальный коэффициент
выражается через биномиальный коэффициент ![]() (см. например, [12, C. 163]) как
(см. например, [12, C. 163]) как ![]()
Группируя слагаемые, входящие в правую часть формулы (6), получим компактную формулу для составного двухточечного многочлена Hm(ξ), построенного для периодической функции:
Из представления (7) наглядно видно, что двухточечный многочлен для периодической функции представляется в виде модифицированного многочлена Тейлора, построенного в заданной точке. Модификация состоит в том, что каждый член многочлена Тейлора умножается на соответствующую функцию влияния ![]() .
.
Многочлен Hm(ξ) с использованием (7) и (8) может быть также записан в виде:
где координатные функции ![]() , являясь единственными сомножителями в (9), которые зависят от переменной ξ, представляются в виде:
, являясь единственными сомножителями в (9), которые зависят от переменной ξ, представляются в виде:
Таблица 1 – Формулы для Hm(ξ)
На рис. 1 для примера представлены зависимости функций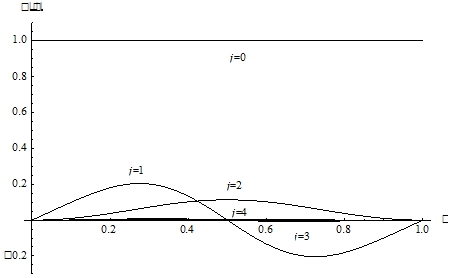
Рис. 1 – Зависимость при j=0-4 и для m=4
На рис. 2 представлены эти же зависимости, выполненные с использованием логарифмической шкалы по оси ординат, и, соответственно, на рисунке показаны графики модуля этих функций, т.е. ![]() .
.
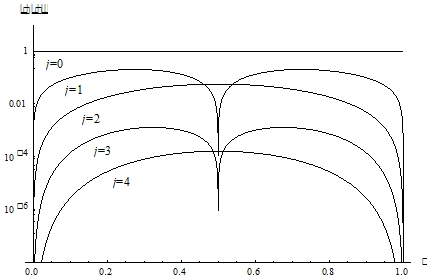
Рис. 2 – Зависимость
Из рисунка видно, что функции ![]() при четных значениях j принимают положительные значения и имеют максимум в середине отрезка, который монотонно убывает с увеличением j. Функции
при четных значениях j принимают положительные значения и имеют максимум в середине отрезка, который монотонно убывает с увеличением j. Функции ![]() при нечетных значениях j до середины отрезка принимают положительные значения, обращаются в нуль в середине отрезка и имеют отрицательные значения во второй половине отрезка, при этом максимум модуля функции также монотонно убывает с увеличением j.
при нечетных значениях j до середины отрезка принимают положительные значения, обращаются в нуль в середине отрезка и имеют отрицательные значения во второй половине отрезка, при этом максимум модуля функции также монотонно убывает с увеличением j.
- Остаточный член и его оценка
Для определения погрешности представления периодической функции составным двухточечным многочленом необходимо определить остаточный член приближения и сделать его оценку. Вследствие выбора способа аппроксимации в виде составных многочленов, выраженного преобразованием (3), исследование остаточного члена приближения периодической функции на всей области может быть ограничено рассмотрением этого члена только на отрезке [x0, x0+T].
Остаточный член r(x), определенный как разность между заданной периодической функцией и многочленом H(x)
| r(x)=f(x)-H(x) | (12) |
где ![]() , т.е. η – некоторая внутренняя точка отрезка [x0, x0+T].
, т.е. η – некоторая внутренняя точка отрезка [x0, x0+T].
С использованием переменной ξ, определенной (3), остаточный член двухточечного представления согласно формуле (13), может быть записан в виде:
| δ(x)=|r(x)|, | (15) |
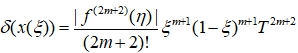
Пусть производная функции порядка 2m+2 на интервале (-∞,∞) ограничена некоторой константой M2m+2 >0, т.е. считаем, что
Из того, что ![]() (например, [10, с. 1098]), и из формулы (18) следует, что погрешность приближения функции δ(x) удовлетворяет соотношению
(например, [10, с. 1098]), и из формулы (18) следует, что погрешность приближения функции δ(x) удовлетворяет соотношению ![]() , где оценка погрешности Δ выражается соотношением
, где оценка погрешности Δ выражается соотношением
Теорема 1. Пусть периодическая функция f(x) с периодом T определена на интервале (-∞<x<∞) и имеет достаточный набор производных на этом интервале. Пусть также в некоторой точке x0 интервала (-∞,∞) заданы значения функции f(x) и ее производных до порядка m включительно:
![]()
Тогда функция f(x) может быть представлена в виде
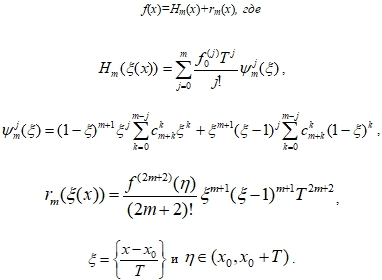
Следствие. Пусть производная функции порядка 2m+2 на интервале (-∞,∞) ограничена некоторой константой M2m+2>0, т.е. выполняется условие
![]()
Тогда для погрешности δ(x) аппроксимации функции имеет место
![]()
где оценка погрешности Δ выражается соотношением
![]()
Действительно, эта формула для оценки погрешности Δ следует из (18) и из того, что
![]()
Доказательство этой формулы приведено, например, в [10, C. 1098].
- Сходимость приближений функции
Если функция имеет неограниченное число производных, то для нее может быть построена последовательность приближающих ее многочленов.
Исследуем условия, при которых последовательность составных двухточечных многочленов Hm(x) сходится к функции f(x) при ![]() .
.
Из формулы (12) следует, что функцию f(x) можно записать как:
| f(x)=Hm(x)+rm(x). | (20) |
Из представления (20) видно, чтобы последовательность двухточечных многочленов Hm(x) сходилась к функции f(x), необходимо и достаточно, чтобы для всех x имело место (см. [13, C. 549])
![]()
При условии, когда рост производных ограничен некоторой показательной функцией их порядка, имеет место достаточный признак сходимости.
Теорема 2. Пусть периодическая функция f(x) и все ее производные ограничены в совокупности на интервале (-∞<x<∞) показательной функцией их порядка j, т.е существуют такая постоянные M>0 и q>0 , такие, что для всех и всех j=0,1,… имеет место
Тогда на этом интервале функция f(x) представляется сходящейся последовательностью соответствующих ей составных двухточечных многочленов Hm(ξ(x)), т.е.
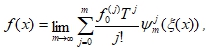 где функции
где функции что и означает в соответствии с (20), что имеет место доказываемое утверждение (22) теоремы.
- Результаты численных экспериментов
Пример 1. Как известно, функция f(x) = sin x является периодической функцией, которая имеет период T=2π. Производные этой функции вычисляются по формуле: (см. например [13, C. 149]):
Таблица 2 – Выражения для многочлена Hm(ξ)
На рис. 3 приведены графики многочленов Hm(x), для m = 0,1,2,3,4. Здесь же для сравнения представлен график функции f(x) = sin x, обозначенный пунктирной линией.
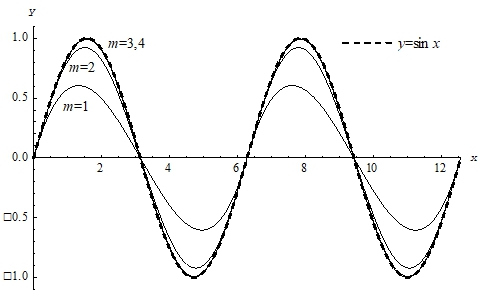
Рис. 3 – Приближение функции f(x) = sin x
Из рисунка видно, что аппроксимирующие многочлены приближаются к данной функции при увеличении m. На рис. 4 показаны графики погрешности приближения δ(x), которая определена по формуле| δ(x)=|f(x)-Hm(x)| | (28) |
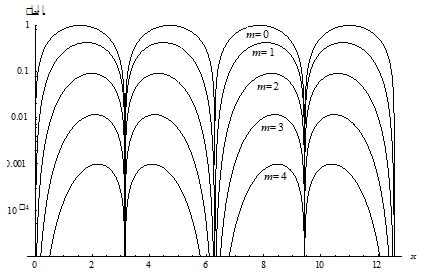
Рис. 4 – Погрешность приближения δ(x)
Из графиков, представленных на рисунке, видно, что погрешность δ(x) также является периодической функцией с те же периодом, что и заданная функция, обращается в ноль при xk=2πk, k=0, ±1,±2... и в данном случае монотонно уменьшается с возрастанием m.
В таблице 3 представлены в числовой форме значения многочлена Hm, его погрешности δm и ее оценки Δm для значения x = π/2, при котором функция y = sin x принимает максимальное свое значение.
Таблица 3 – Значения многочлена Hm, его погрешности δm и ее оценки Δm
| s | m | Hm(π/2) | δm | Δm |
| 1 | 0 | 0.000000000000 | 1.00000000000 | 4.93480220054 |
| 3 | 1 | 0.589048622548 | 0.410951377452 | 4.05871212642 |
| 5 | 2 | 0.920388472731 | 0.079611527269 | 1.33526276885 |
| 7 | 3 | 0.991217827278 | 0.008782172722 | 0.23533063036 |
| 9 | 4 | 0.999377014126 | 0.000622985874 | 0.02580689139 |
| 11 | 5 | 0.999969215729 | 0.000030784271 | 0.00192957431 |
| 13 | 6 | 0.999998879582 | 0.000001120418 | 0.00010463810 |
| 15 | 7 | 0.999999968709 | 0.000000031291 | 0.00000430307 |
Из таблицы 3 видно, что при увеличении m значение многочлена Hm стремятся к точному значению функции y = sin x, погрешность δm стремится к нулю и оценка погрешности Δm, ограничивая саму погрешность сверху, также стремится к нулю.
Пример 2. Рассмотрим периодическую функцию вида f(x) = sin 2x – cos x, которая также имеет период T=2π. Производные этой функции определяются соотношением:
Подставляя производные этой функции в формулы, представленные в табл. 2, получим соответствующие выражения для аппроксимирующих многочленов.
На рис. 5 представлены графики приближающих многочленов для m=2,4,6,8. При увеличении m аппроксимирующие многочлены также стремятся к заданной функции.
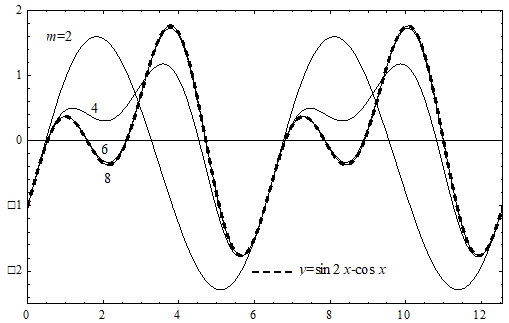
Рис. 5 – Приближение функции f(x) = sin 2x – cos x
На рис. 6 показаны графики погрешности приближения δ(x), полученной по формуле (28) для различных значений параметра m.
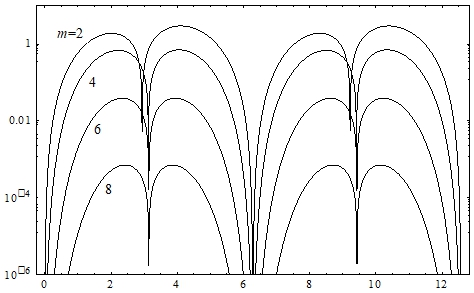
Рис. 6 – Погрешность приближения δ(x)
Из представленных графиков видно, что погрешность приближения δ(x) имеет более сложный характер, но также стремится к нулю при возрастании m. Это объясняется выполнением достаточного условия теоремы 2 о сходимости последовательности аппроксимирующих многочленов.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Романовский П.И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа / Романовский П.И.. – М.: Наука. Гл. ред. физ.-мат. лит., 1980. – 336 с.
- Архипов Г.И.. Лекции по математическому анализу. / Архипов Г.И., Садовничий А.А., Чубариков В.Н.– М.: Высшая школа, 1999. – 695с.
- Кудрявцев Л.Д. Курс математического анализа. т. II. / Кудрявцев Л.Д.– М.: Высшая школа, 1981. – 584с.
- Колмогоров А.Н. Элементы теории функций и функционального анализа. / Колмогоров А.Н., Фомин С.В.– М.: Наука. Гл. ред. физ.-мат. лит., 1989. – 624 с.
- Березин И.С. Методы вычислений. Т. 1 / Березин И.С., Жидков Н.П. – М.: Физматлит, 1962.– 464 с.
- Хемминг Р.В. Численные методы для научных работников и инженеров. / Хемминг Р.В. – М.: Наука. Гл. ред. физ.-мат. лит., 1972. – 400 с.
- Ланцош К. Практические методы прикладного анализа. / Ланцош К. – М.: Гос. изд. физ.-мат. лит., 1961. – 524 с.
- Микеладзе Ш.Е. Численные методы математического анализа./ Микеладзе Ш.Е. М.: Гостехтеориздат, 1953. – 528 с.
- Воробьев Н.Н. Теория рядов / Воробьев Н.Н. – М.: Наука. Гл. ред. физ.-мат. лит., 1986. – 406 с.
- Шустов В.В. О приближении функций двухточечными интерполяционными многочленами Эрмита / Шустов В.В. // ЖВММФ, 2015, № 7, С. 1091-1108.
- Шустов В.В. Аппроксимация функций несимметричными двухточечными многочленами Эрмита и ее оптимизация / Шустов В.В. // ЖВММФ, 2015, № 12, С. 1999-2014.
- Бронштейн И.Н. Справочник по математике для инженеров и учащихся втузов / Бронштейн И.Н., Семендяев К.А. СПб.: Изд. Лань, 2010 – 608 с.
- Кудрявцев Л.Д. Математический анализ. Т. 1./ Кудрявцев Л.Д. – М.: Высшая школа, 1970. – 592с.
- Шустов В.В. О приближении периодических функций составными двухточечными многочленами Эрмита / Шустов В.В. // Современные методы теории функций и их приложения: материалы 18 Саратовской зимней математической школы / Саратовский гос. ун-т. – Саратов, 2016. – С. 338-341.
Список литературы на английском языке / References in English
- Romanovskii P. I. Ryady Fur'e. Teoriya polya. Analiticheskie i spetsial'nye funktsii. Preobrazovanie Laplasa [Fourier series. Field theory. Analytical and special functions. Laplace Transformation] / Romanovskii P. I. . Moscow, Nauka, 1980, 336 p. [in Russian].
- Arkhipov I. Lektsii po matematicheskomu analizu [Lectures on mathematical analysis] / Arkhipov G. I., Sadovnichii A. A., Chubarikov V. N.. Moscow, Vysshaya shkola, 1999, 695 p. [in Russian].
- Kudryavtsev D. Kurs matematicheskogo analiza [Course of mathematical analysis] / Kudryavtsev L. D. . Vol II. Moscow, Vysshaia shkola, 1981. 584 p. [in Russian].
- Kolmogorov N. Elementy teorii funktsii i funktsional'nogo analiza [Elements of the theory of functions and functional analysis] / Kolmogorov A. N., Fomin S. V. . Moscow, Nauka , 1989, 624 p. [in Russian].
- Berezin I. S. Computing Methods. / I. S. Berezin, N. P. Zhidkov. Vol. 1 – Pergamon: Oxford, 1965. – 464 P.
- Hamming R.W. Numerical Methods for Scientists and Engineers. Mc Graw-Hill Book Company / Hamming R.W, Inc New York, 1962.
- Lanczos Applied analysis / Lanczos K. . Prentice Hall, 1956.
- Mikeladze E. Chislennye metody matematicheskogo analiza [Numerical methods of mathematical analysis] / Mikeladze Sh. E.. Moscow, Gostekhteorizdat, 1953. 528 p. [in Russian].
- Vorob'ev N. Teoriya ryadov [The theory of series] / Vorob'ev N. N. Moscow, Nauka, 1986, 406 p. [in Russian].
- Shustov V. V. Approximation of functions by two-point Hermite interpolating polynomials / V. V. Shustov // Computational Mathematics and Mathematical Physics. – 2015. – 55. – No 7. – P. 1077–1093. doi: 10/1134/S0965542515040156
- Shustov V. V. Approximation of functions by asymmetric two-point Hermite polynomials and its optimization / V. V. Shustov // Computational Mathematics and Mathematical Physics. – 2015. – Vol. 55. – No – P. 1960–1974. doi: 10/1134/S0965542515120155
- Bronshtein N. Spravochnik po matematike dlya inzhenerov i uchashchikhsya vtuzov [Handbook of mathematics for engineers and technical colleges students] / Bronshtein I. N., Semendiaev K. A. St Peterburg, Izd. Lan', 2010, 608 p. [in Russian].
- Kudriavtsev L. D. Matematicheskii analiz [Mathematical analysis] / Kudriavtsev L. D. . Vol. 1. Moscow, Vysshaia shkola, 1970, 592 p. [in Russian].
- Shustov V. O priblizhenii periodicheskikh funktsii sostavnymi dvukhtochechnymi mnogochlenami Ermita [On the Approximation of Periodic Functions by Composite Two-Point Hermite Polynomials] / Shustov V. V. Sovremennye metody teorii funktsii i ikh prilozheniya : materialy Saratovskoi zimnei matemicheskoi shkoly. [Modern Methods of Function Theory and Aplication] : Proc. Saratov Winters School], Saratov, 2016, pp. 338-341 [in Russian].


