АППРОКСИМАТИВНЫЕ СВОЙСТВА ПРОКСИМИНАЛЬНЫХ ПОДПРОСТРАНСТВ БЕСКОНЕЧНОЙ РАЗМЕРНОСТИ

АППРОКСИМАТИВНЫЕ СВОЙСТВА ПРОКСИМИНАЛЬНЫХ ПОДПРОСТРАНСТВ БЕСКОНЕЧНОЙ РАЗМЕРНОСТИ

Научная статья

Федоров В.М. *

ORCID: 0000-0002-4586-6591,

МГУ им. М.В. Ломоносова, Москва, Россия

* Корреспондирующий автор (vferdorov[at]rambler.ru)

Аннотация

Для подпространств L бесконечной размерности в банаховом пространстве  получены характеристические свойства существования элементов наилучшего приближения. В качестве приложения доказывается, что в пространстве непрерывных функций на связном хаусдорфовом компакте T чебышевское подпространство   бесконечной размерности, у которого аннулятор  сепарабельный и  содержит минимальное тотальное подпространство, является гиперплоскостью  строго положительного функционала .

Ключевые слова: аннулятор, сепарабельность, размерность, коразмерность,  проксиминальное подпространство, чебывшевское подпространство.

APPROXIMATIVE PROPERTIES OF PROXIMAL SUBSPACES OF INFINITE DIMENSION

Research article

Fedorov V.M. *

ORCID: 0000-0002-4586-6591,

Faculty of Mechanics and Mathematics, Lomonosov Moscow State University, Moscow, Russia

* Corresponding author (vferdorov[at]rambler.ru)

Abstract

For subspaces L of infinite dimension in a Banach space, the authors obtained the characteristic properties of the existence of elements of the best approximation. As an application, they prove that, in the space  of continuous functions on a connected Hausdorff compactum T, the Chebyshev subspace  of infinite dimension, the annihilator  of which is separable and contains the minimal total subspace, is a hyperplane  of a strictly positive functional .

Keywords: annihilator, separability, dimension, codimension, proximal subspace, Chebyshev subspace.

Введение

Пусть  есть замкнутое подпространство банахова пространства E. Обозначим через  факторпространство смежных классов  по подпространству L и через  норму в факторпространстве . Подпространство  называется проксиминальным,  если для любого  множество  не пусто, и называется чебышевским, если для любого  множество  состоит из одного элемента.

Используя компактность конечномерного шара, можно показать, что всякое конечномерное подпространство  является проксиминальным. Проблема характеристики бесконечномерных проксиминальных подпространств  является достаточно трудной задачей и решена только для подпространств конечной коразмерности [1, 2, 3]. Указанные там характеристики является обобщением результатов, полученных ранее для классических нормированных пространств, таких, как пространство непрерывных функций на хаусдорфовом компакте  интегрируемых функций по Лебегу на измеримом пространстве  с -конечной мерой μ [4], [5], [6]. Нашей задачей является нахождение необходимых и достаточных условий проксиминальности для подпространств, имеющих бесконечную размерность, у которых  аннулятор  содержит минимальное, замкнутое и тотальное подпространство. В частности, для подпространств, у которых аннулятор является рефлексивным.

Основные результаты

Аннулятор  подпространства L изометричен сопряженному пространству  [7, С. 110] и его шар радиуса , т.е.  множество , является слабо* компактным в сопряженном  пространстве * [8, С. 459]. Далее мы будем предполагать, что аннулятор  является сепарабельным и обозначим через  единичный шар в  *.

Подпространство  называется тотальным, если из условия . Тотальность  равносильна его слабой* плотности в * [8, С. 457; 9, С. 198]. Характеристикой  подпространства  называется верхняя грань чисел , т.ч. слабое* замыкание  содержит шар  [9, С. 275]. Подпространство  называется минимальным, если оно замкнуто и тотально, при этом не имеет собственных замкнутых и тотальных подпространств.

Лемма 1

Если аннулятор содержит минимальное, замкнутое и тотальное подпространство , то для любого  он содержит также такое минимальное, замкнутое и тотальное подпространство .

Доказательство. Известно [9, С. 275], что пространство  тогда и только тогда изоморфно сопряженному пространству , когда существует минимальное, замкнутое и тотальное подпространство  положительной характеристики.  При этом изоморфизм является каноническим, т.е. задается по формуле  ограничения функционала Дирака  на подпространство F. В этом случае, пространство  изоморфно прямой сумме .

Пусть . Рассмотрим ненулевой функционал , не принадлежащий аннулятору  и образу  канонического вложения . Тогда линейная оболочка  задает такое подпространство в *, которое содержит α и его аннулятор в   равен нулю. Так как . Поэтому  минимальным, замкнутым и тотальным  подпространством положительной характеристики [9, С. 275].

Обозначим через  пространство непрерывных и ограниченных функций на множестве T и определим отображение . Рассмотрим образ оператора .  Поскольку множество  выпукло, симметрично и поглощает M, где S есть единичный шар E, то функционал Минковского  определяет норму в подпространстве M.  При этом .

Лемма 2

Отображение  задает слабо компактный оператор, его факторотображение является изометрическим оператором, норма в M эквивалентна индуцированной норме из  а если характеристика подпространства F равна  , то эти нормы совпадают.  

Доказательство. Поскольку , то оператор ограничен.  Пусть обозначает второй сопряженный оператор. Если , то существует ограниченная сеть , которая слабо* сходится к f  [8, С. 460]. Поэтому в силу слабой* непрерывности оператора Ф** [8, стр. 515]

где . Здесь  обозначает функционал Дирака  на сопряженном пространстве E*. Поскольку единичный шар S** слабо* компактный, то его образ  будет слабо* компактным в пространстве .  Применяя  формулу  [8, С. 516] и слабую* плотность множества  [8, С. 460], где каноническое вложение  во второе сопряженное пространство E**,  получим, что образ  является относительно слабо компактным. Таким образом, оператор Ф  является слабо компактным.

Если , то для любого  существует . Тогда имеем  и значит . С другой стороны, пусть . Тогда существует . Тогда в силу тотальности подпространства  мы получим включение  и, следовательно, имеем . Таким образом, имеет место равенство .

Поскольку норма пространства М совпадает с нормой пространства  и при выполняется включение , то имеют место неравенства .

Поэтому норма в М эквивалентна индуцированной норме из .

Замечание

Выполняя композицию сопряженного отображения и естественной изометрии , получим изометрию  по формуле . Это замечание позволяет напрямую доказать изометрию . В самом деле, имеем .

Пусть  образует минимальное, замкнутое и тотальное подпространство. Тогда каноническое отображение , заданное формулой , является изоморфизмом банаховых пространств  и , а также в их слабых* топологиях   соответственно [10, С. 246].

Поэтому отображение  является также  изоморфизмом пространств в соответствующих топологиях.  Следовательно, имеем  и отображение ограничения функций на множество  будет изоморфизмом. При этом пространство N* естественно отождествляется с пространством M, в котором  сходимость последовательности функций в слабой* топологии  равносильна ее ограниченности и поточечной сходимости на множестве T.

Поскольку в силу теоремы Банаха-Штейнгауза [11, С. 283]  пространство N* секвенциально слабо* полно, то пространство M секвенциально полно в слабой* топологии . Если последовательность  сходится в слабой* топологии , то ее поточечный предел  удовлетворяет неравенству  и принадлежит . Поскольку образ единичного шара при каноническом отображении  является всюду плотным в в слабой* топологии в единичном шаре F*[12, С. 320], то B плотно в слабой* топологии в единичном шаре N*. Если характеристика  , то множество  не может быть слабо* компактным и слабо* полным в топологии .

Теорема 1

Для замкнутого подпространства , у которого размерность  и коразмерность , следующие  условия эквивалентны:

1. подпространство L является проксиминальным в пространстве E;
2. множество 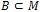является замкнутым в слабой топологии  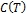для всякого замкнутого и тотального  подпространства  ;
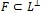3. множество 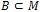 является полным в слабой топологии  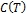для всякого  минимального, замкнутого и тотального подпространства ;
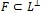4. множество 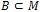 является компактным в слабой топологии  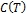для всякого минимального, замкнутого и тотального подпространства ;                            
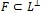5. если функционал 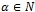и последовательность функций  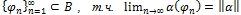, 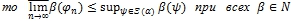и для любого минимального, замкнутого и тотального подпространства .

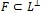Здесь  обозначает экстремальное множество, т.е. множество элементов, в которых функционал  достигает своей нормы.

Доказательство. Покажем, что из условия a) следует b). Так как множество B является выпуклым, то его замкнутость в слабой топологии пространства  вытекает из замкнутости в топологии пространства M, а поскольку по лемме 2 индуцированная норма из  эквивалентна норме M, то достаточно доказать замкнутость множества B в пространстве M.  Допустим, что  замыкание  берется в пространстве M. Тогда по лемме 2 получим  и не существует элемента . Так как в силу тотальности F равенство  равносильно включению , то для всякого  получим . Следовательно,  , т.е. множество пусто, что противоречит условию a).

Покажем, что из условия b) следует a). Из слабой замкнутости множества B в пространстве  следует его замкнутость в пространстве , а поскольку по лемме 2 индуцированная норма из  эквивалентна норме в M, то множество B является замкнутым в пространстве M. Пусть . Применяя по лемму 2 и замкнутость множества B в пространстве M, мы имеем включение . Следовательно, существует такой , что . Поэтому в силу тотальности подпространства  имеет место включение . Отсюда следует, что . Таким образом, подпространство L является проксиминальным.

Покажем, что условие b) равносильно каждому из условий c) и d). Так как пространство сепарабельно и норма M эквивалентна индуцированной норме из , то сопряженное пространство M* будет замкнутой линейной оболочкой последовательности непрерывных функционалов  из пространства . Следовательно, для доказательства слабой компактности множества    достаточно показать, что любая последовательность  содержит такую подпоследовательность , для которой последовательность чисел  сходится при всех .

Для доказательства этого утверждения применяем диагональный метод Кантера. Сначала из последовательности чисел  выбираем сходящуюся подпоследовательность . Затем из последовательности чисел   выбираем сходящуюся подпоследовательность  , и так далее продолжаем по индукции. В результате этого образуется бесконечная таблица функций , из которой мы выбираем диагональные элементы . Тогда последовательность  сходится при всех .

Применяя критерий слабой сходимости в пространстве M, мы получим, что существует предел . В частности, существует предел . Так как по теореме Банаха-Штейнгауза [11, С. 283]  пространство N* секвенциально слабо* полно, то пространство M секвенциально полно в слабой* топологии , а - поэтому функция .  В силу условия слабой замкнутости множества B в пространстве   получим . Таким образом, из условия b) вытекает каждое из условий c) и d).

Обратно, если выполняется c) или d), то из слабой полноты множества B в пространстве  или из слабой компактности B в пространстве  вытекает слабая замкнутость множества B в пространстве , т.е. имеет место b).

Покажем, что из условия b) следует e). Предположим, что существует такая  последовательность , что , но функционал , удовлетворяет неравенству . Применяя свойство d), мы можем выбрать такую подпоследовательность  при всех  и . Докажем, что .

Пусть . Тогда, если , то выполняется строгое неравенство , поскольку

.

Пусть . Тогда, если , то также выполняется строгое неравенство , поскольку .

Следовательно, мы имеем . Таким образом, получили противоречие.

Покажем, что из e) следует b). Пусть , тогда  и существует  последовательность, т.ч. . По теореме Хана-Банаха [11, С. 232] существует . Тогда по лемме 1 можно считать, что  , и значит .

Так как  и  являются выпуклыми, непересекающимися и слабо* компактными подмножествами множества B, то выпуклая оболочка  является слабо* компактным подмножеством B [9, С. 104]. Поэтому для доказательства условия b) достаточно показать, что . Предположим, что это включение не выполняется, т.е. .

По теореме отделимости существует такой  . Применяя конструкцию доказательстве леммы 1, можно считать, что  . Тогда имеем , что невозможно по условию, и мы получили противоречие.

Теорема 2

Пусть аннулятор  чебышевского подпространства  бесконечной размерности в пространстве непрерывных функций на связном хаусдорфовом компактном множестве T  содержит минимальное, замкнутое и тотальное подпространство . Тогда , размерность  и подпространство L образует гиперплоскость , для которой  является строго положительным функционалом.

Доказательство. Так как  является чебышевским подпространством, то существует такая функция , что  при всех . В силу теоремы Хана-Банаха [11, С. 232] найдется функционал . При помощи леммы 1 мы можем считать, что .

Поскольку факторпространство  изоморфно сопряженному пространству  и аннулятор  изометрически изоморфен  сопряженному пространству, то экстремальное множество  функционала α будет выпуклым и слабо* компактным множеством в пространстве . По теореме Крейна-Мильмана [8, С. 477] существует крайняя точка  в множестве . Тогда  является крайним подмножеством границы единичного шара  [2, С. 903], а поскольку подпространство  является чебышевским, то это множество состоит из одной точки, которая будет крайней точкой границы шара S. В силу связности компакта  существуют только две крайние точки  на границе шара S и по построению . Поэтому можно считать функцию  крайней точкой границы шара S.

По теореме Рисса-Маркова существует -аддитивная борелевская мера μ на компакте T, т.ч.  при всех  [8, С. 288]. Так как , то мера μ неотрицательна. Докажем, что . Предположим, что некоторый  элемент  не принадлежит L. Поскольку подпространство L является проксиминальным, то, вычитая из φ элемент наилучшего приближения подпространством L, можно считать, что . Тогда, применяя аналогичные рассуждения, как и выше, мы получим, что . Это противоречит условию . Таким образом, .

Если , где функция  и не равна нулю, то , что противоречит единственности наилучшего приближения [12, С. 649]. Таким образом, функционал  является строго положительным.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Cписок литературы / References

1. Singer I. On best approximation in normed linear spaces by elements of subspaces of finite codimension / I. Singer // Rev. Roum. Math. Pures Appl.    17.  №8.  P. 1245-1256.
2. Godini G. Characterizations of proximinal subspaces in normed linear spaces / G. Godini // Rev. Roum. Math. Pures Appl.  18.  №6.  P. 901-906.
3. Indumathi V. Proximinal subspaces of finite codimension in general normed linear spaces / V. Indumathi // London Math. Soc. 1982.  45.  №3.  P. 435-455.
4. Гаркави А. Л. О наилучшем приближении элементами бесконечномерных подпространств одного класса / А. Л. Гаркави // Мат. сборник.     62.  №1 (104).  С. 104-120.
5. Гаркави А. Л. Аппроксимативные свойства подпространств конечного дефекта в пространстве непрерывных функций / А. Л. Гаркави // Доклады АН СССР.    155.  С. 513-516.
6. Гаркави А. Л. Задача Хелли и наилучшее приближение в пространстве непрерывных функций. / А. Л. Гаркави // Известия АН СССР, сер. мат. 31. №3.  С. 641-656.
7. Рудин У. Функциональный анализ / У. Рудин // Москва: МИР, 1975. 445с.
8. Данфорд Н. Линейные операторы. Часть 1: Общая теория. / Н. Данфорд, Дж. Шварц // Москва: ИЛ, 1962.
9. Бурбаки Н. Топологические векторные пространства / Н. Бурбаки // Москва: ИЛ,   411 с.
10. Goldberg S. On Dixmiers Theorems Concerning Conjugate Spaces / S. Goldberg // Math. Annelan    147.  P. 244-247.
11. Канторович Л. В. Функциональный анализ / Л. В. Канторович, Г. П. Акилов // Москва: Наука, 1984.  752 с.
12. Singer I. On a theorem of J. D. Weston / I. Singer // Jour. London Math. Soc.  34.  P. 320-324.
13. Phelps R. Cebysev subspace of finite codimension in / R. Phelps // Jour. Math.  1963.  13.  №2.  P. 647-655.

Список литературы на английском языке / References in English

1. Singer I. On best approximation in normed linear spaces by elements of subspaces of finite codimension / I. Singer // Rev. Roum. Math. Pures Appl.    17.  №8.  P. 1245-1256 [in English].
2. Godini G. Characterizations of proximinal subspaces in normed linear spaces / G. Godini // Rev. Roum. Math. Pures Appl.   18.  №6.  P. 901-906 [in English].
3. Indumathi V. Proximinal subspaces of finite codimension in general normed linear spaces / V. Indumathi // London Math. Soc. 1982.  45.  №3.  P. 435-455 [in English].
4. Garkavi A. L. O nailuchshem priblizhenii elementami beskonechnomernykh podprostranstv odnogo klassa [On the best approximation by elements of infinite dimensional subspaces of one class] / A. L. Garkavi // sbornik. [Mat. Compilation]. 1963.   62.  №1 (104).  P. 104-120 [in Russian].
5. Garkavi A. L. Approksimativnyye svoystva podprostranstv konechnogo defekta v prostranstve nepreryvnykh funktsiy [Approximation properties of subspaces of a finite defect in the space of continuous functions] / A. L. Garkavi // Doklady AN SSSR [Reports of the USSR Acad. of Scienc.]. – 1964. P. 513-516 [in Russian].
6. Garkavi A. L. Zadacha Khelli i nailuchsheye priblizheniye v prostranstve nepreryvnykh funktsiy [Helly's problem and the best approximation in space continuous functions] / A. L. Garkavi // Izvestiya AN SSSR, ser. mat. [Proceedings of the Acad. of Scienc.  USSR, ser. math.] – 1967.    №3.  P. 641-656 [in Russian].
7. Rudin U. Funktsional'nyy analiz [Rudin W. Functional analysis] / U. Rudin // Moskva: MIR [Moscow: MIR], 1975. – 445 p. [in Russian].
8. Danford N. Lineynyye operatory. Chast' 1: Obshchaya teoriya [Dunford N., Schwartz J. Linear Operators. Part 1: General theory] / N. Danford, Dzh. Shvarts // Moskva: IL [Moscow: IL]. – 896 p. [in Russian].
9. Burbaki N. Topologicheskiye vektornyye prostranstva [Bourbaki N. Topological vector spaces] / N. Burbaki // Moskva: IL [Moscow: IL], 1959. – 411 p. [in Russian].
10. Goldberg S. On Dixmiers Theorems Concerning Conjugate Spaces / S. Goldberg // Math. Annelan    147.  P. 244-247. [in English].
11. Kantorovich L. V. Funktsional'nyy analiz [Functional Analysis] / L. V. Kantorovich, G. P. Akilov // Moskva: Nauka [Moscow: Science], 1984. – 752 p. [in Russian].
12. Singer I. On a theorem of J. D. Weston / I. Singer // Jour. London Math. Soc. 34.  P. 320-324 [in English].
13. Phelps R. Cebysev subspace of finite codimension in / R. Phelps // Jour. Math.  1963.  13.  №2.  P. 647-655 [in English].