МОДЕЛИРОВАНИЕ ТЕЧЕНИЙ ЖИДКОСТИ В ПРОНИЦАЕМЫХ СЛОЯХ ГРУНТА С ПОМОЩЬЮ РЕШЕНИЯ ЗАДАЧ ХЕЛЕ-ШОУ

Шерыхалина Н.М.¹, Зарипов А.А.²

¹ ORCID: 0000-0002-2808-1311, Доктор технических наук,

² ORCID: 0000-0002-6541-4680, Аспирант,

^1,2 Уфимский государственный авиационный технический университет, Уфа, Россия

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 17-07-00356)

МОДЕЛИРОВАНИЕ ТЕЧЕНИЙ ЖИДКОСТИ В ПРОНИЦАЕМЫХ СЛОЯХ ГРУНТА С ПОМОЩЬЮ РЕШЕНИЯ ЗАДАЧ ХЕЛЕ-ШОУ

Аннотация

Решается задача подземной гидродинамики для моделирования утечек воды при создании гидросооружений типа водохранилищ. Сжимаемостью жидкости и грунта пренебрегается, что позволяет в качестве модели использовать задачу Хеле-Шоу. Разработан численно-аналитический метод решения задачи с применением теории функций комплексного переменного. Рассмотрены два режима изменения давления: скачкообразное и линейное по времени с ограничением. Решены задачи с различной конфигурацией границ.

Ключевые слова: подземная гидродинамика; несжимаемая жидкость; плоская задача; комплексный потенциал.

Sherykhalina N.M.¹, Zaripov A.A.²

¹ ORCID: 0000-0002-2808-1311, PhD in Engineering,

² ORCID: 0000-0002-6541-4680, PhD student,

^1,2 Ufa State Aviation Technical University, Ufa, Russia

This work was supported by the Russian Foundation for Basic Research (project code 17-07-00356)

MODELING OF LIQUID FLOWS IN PERVIOUS GROUND LAYERS WITH USE OF HELE-SHAW SOLUTION

Abstract

The problem of underground hydrodynamics is solved for water leaks modeling during the construction of hydro-constructions of reservoir type. The compressibility of the liquid and soil is neglected, which allows us to use the Hele-Shaw problem as a model. A numerical-analytical method for solving the problem using the theory of functions of a complex variable is developed. Two modes of pressure change are considered: jumplike and linear in time with constraint. Problems with different border configurations were solved.

Keywords: underground hydrodynamics; incompressible fluid; two-dimensional problem; complex potential.

Рассмотрим плоскую задачу о течении жидкости в водопроницаемом слое грунта, обусловленном наличием столба жидкости в резервуаре или водохранилище. До подъема уровня водохранилища проницаемый слой считается сухим, и давление в нем равно атмосферному из-за наличия близко расположенного оврага или канала (рис. 1).

Для границ с очень сложной криволинейной формой можно предложить метод декомпозиции задачи (рис. 2). Для этого область течения условно разрезается на несколько подобластей непроницаемыми пластинами. Для уменьшения погрешности, связанной со спрямлением линий тока можно использовать наложение отдельных подобластей, т. е. соседние подобласти могут пересекаться. Ширина расчетной области – L.

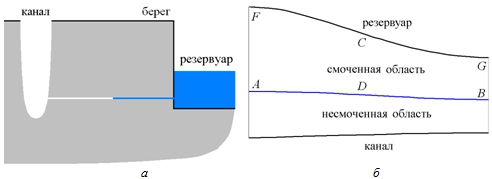
Рис. 1 – Схема течения: а – вертикальный разрез: физической; б – горизонтальный разрез

 

Жидкость и грунт считаются несжимаемыми, предполагается выполнение закона Дарси

  (1)

где V – скорость жидкости; P V – давление в потоке; k – коэффициент фильтрации.

Тем самым, течение считается соленоидальным и потенциальным, поэтому для решения задачи можно использовать методы теории функций комплексного переменного (ТФКП).

Необходимо отметить, что большой вклад в исследование подобных задач, которые относятся к задачам Хеле-Шоу [1], с помощью методов ТФКП внесла П.Я. Полубаринова-Кочина [2], [3]. Но при этом большее внимание уделялось исследованию стационарных решений. Решение нестационарных задач позволяет определить многие дополнительные параметры, в том числе время установления стационарного процесса с заданной точностью. В данной работе нестационарная задача решается методом, аналогичным разработанному для решения задач моделирования электрохимического формообразования [4].

Пусть . Образом области течения на плоскости комплексного потенциала  – потенциал, Ψ – функция тока) является прямоугольник ширины  (ΔP=P_FCG-P_ADB – разность давлений на границах) и высоты Q, где Q – расход жидкости, протекающий в ячейке (рис. 2,а). Линиям тока FA и GB соответствуют горизонтальные отрезки. При этом величина скорости жидкости определяется производной .

Пусть L – ширина ячейки (рис. 1,б). Перейдем к безразмерным координатам x, y, и времени τ

   (2)

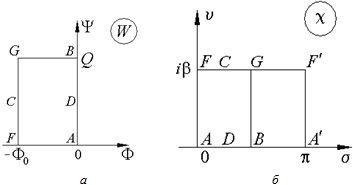
Рис. 2 – Формы образов МЭП: а – на плоскости комплексного потенциала; б – на параметрической плоскости χ

Согласно (2) и (1)      (3)

Конформно отобразим область МЭП на прямоугольник параметрической плоскости χ (рис. 2, б). Для выполнения условия  на участках границы FA и GB функцию , согласно принципу симметрии, следует аналитически продолжить симметрично отрезку GB (рис. 2,б).

При решении нестационарной задачи Хеле-Шоу методами ТФКП необходимо найти аналитические функции , а также .

Первая задача является задачей определения конформного отображения полосы на криволинейную полосу с периодической (с периодом 2L) зависимостью ординат от абсциссы  на нижней и верхней границе. Функцию  представим в виде

   (4)

где  – периодическая (с периодом p) в смысле ТФКП функция χ, определяющая отличие формы границ МЭП от прямых.

Краевыми условиями для определения аналитической функции  для каждого τ являются равенства

  (5)

  (6)

При условиях (5), (6) аналитическая внутри прямоугольника и непрерывная в его замыкании функция, осуществляющая конформное отображение, в каждый момент времени может быть найдена с помощью интеграла Шварца [5, с. 8]

  (7)

где c₁ – произвольная действительная постоянная (для данной задачи ). Для выполнения условия (6) необходимо, чтобы выполнялось равенство

   (8)

Обозначим . Логарифмические производные тэта – функций вычисляются через быстро сходящиеся ряды [6, с.93].

Функции  при выполнении условия (8) определяются из уравнений

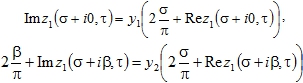   (9)

Функция  получается следующим образом. На границах  в узловых точках  задаются значения  и . Значения ,  в промежуточных между узловыми точках определяются с помощью кубического сплайна, имеющего две непрерывные производные.

Численное интегрирование (7) проводится с помощью двухточечной квадратурной формулы Гаусса 4-го порядка точности относительно параметра . Для интегралов с особенностями вычисляются главные значения. Для ускорения вычислений ряды интерполируются сплайнами.

Численно задача конформного отображения решалась методом коллокаций. В силу симметрии области уравнение формы неподвижной границы (9) удовлетворялось в отдельных точках . Кроме того, требовалось выполнение уравнения (8). На подвижной границе значения  на каждом временном шаге оказываются известными, поэтому искомыми при конформном отображении являются значения . Получаемая при этом система n₁/2+n₂/2+1 нелинейных уравнений относительно параметров  решалась методом Ньютона с регулированием шага.

Вторая задача – определение   решается с помощью конформного отображения

  (10)

(при этом зависимость параметра  определяется в процессе решения задачи).

Решение третьей задачи – определение скорости сдвига границ можно найти с помощью уравнений типа Полубариновой-Галина [7, 8]. Однако это требует решения системы линейных алгебраических уравнений.

Эту задачу можно решить проще. Поскольку в соответствии с (3) сдвиг точек поверхности анода происходит вдоль вектора скорости, то после вычисления значений  для  совершается шаг по времени методом Эйлера

  (11)

Однако, поскольку сдвиг точек происходит по нормали к поверхности анода, то точки, находящиеся на выпуклых в сторону несмоченной поверхности участках границы, на каждом шаге по времени расходятся. Теряется точность, и даже устойчивость. Чтобы этого избежать, предлагается вернуться к частной производной по времени  следующим способом. Поскольку при совершении шага по формуле (11) и решении задачи конформного отображения получаются новые значения , то чтобы вернуться к старым значениям  строятся сплайны ,  и определяются значения

    (12)

Таким образом, осуществляется сдвиг точек вдоль вектора частных производных , что позволяет сохранить точность и устойчивость решения. Далее снова производится сдвиг (11), конформное отображение, пересчет (12) и т. д.

Оценка погрешности численного решения проводилась методом фильтрации результатов вычислений [9, 10] и показала точность около 3-х значащих цифр.

На рис. 3 показаны формы свободной поверхности для значения шага по безразмерному времени Δ_τ=0.05. (Расчет производился при  и Δ_τ=0.0001). Рассмотрены два режима изменения давления: скачкообразное, соответствующее прорыву жидкости через препятствие, (рис. 3,а) и линейное по безразмерному времени τ, связанное с постепенным заполнением резервуара, (, где r=1/25) с ограничением rt≤1 (рис. 3,б). Видно, что свободная граница движется в сторону границы канала и достигает его. После того, как последняя точка фронта достигает границы канала, устанавливается стационарное решение.

В начале процесса при скачкообразном увеличении давления в соответствии с (1) и (2) в одномерном приближении величины локального зазора S и безразмерного зазора s равны

При постепенном заполнении

Эти соотношения помогают найти стартовые конфигурации подвижной границы при расчетах.

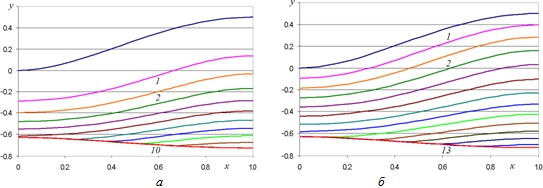
Рис. 3 – Движение фронта потока: а – при скачкообразном изменении давления; б – при линейном изменении давления (D_t=0.05)

 

На рис. 4 приведены аналогичные результаты для другой конфигурации неподвижных границ.

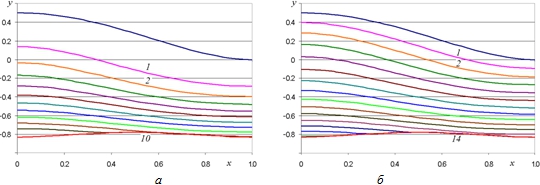
Рис. 4 – Движение фронта потока: а – при скачкообразном изменении давления; б – при линейном изменении давления (D_t=0.05)

  Согласно (2) и (10) расход и безразмерный расход определяются по формулам

На рис. 5 приведены графики зависимостей безразмерного расхода от безразмерного времени.

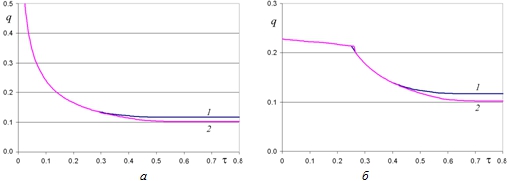
Рис. 5 – Зависимости безразмерного расхода от безразмерного времени: а – для первой конфигурации; б – для второй конфигурации

 

При скачкообразном изменении давления в начальный момент времени расход теоретически бесконечен (при нулевом зазоре), при линейном определяется по формулам

где  – длина неподвижной границы.

Таким образом, в данной работе для определения нестационарной формы границы проникновения жидкости в проницаемый слой грунта предложено использовать численно-аналитический метод, включающий решение задачи Шварца на прямоугольнике с помощью тэта-функций.

С помощью этого метода были рассчитаны границы течения в различные моменты времени при различных формах границ резервуара и канала и двух способах изменения давления в резервуаре.

Список литературы / References

1. Howison S. D. Complex variable methods in Hele-Shaw moving boundary problems / S. D. Howison // Eur. J. Appl. Math. – 1992, Vol. 3. – P. 209-
2. Полубаринова-Кочина П. Я. Теория движения грунтовых вод. 2-е изд. / П. Я. Полубаринова-Кочина. – М.: Наука, – 1977. – 664 с.
3. Ockendon J. R. Kochina and Hele-Shaw in modern mathematics, natural sciences, and technology / J. R. Ockendon, S. D. Howison // J. Appl. Math. Mech. 2002. – Vol. 66, No. 3. – PP. 505–512.
4. Житников В. П. Моделирование электрохимического копирования в ячейке конечной ширины / В. П.Житников, Н.М. Шерыхалина, А.А. Зарипов // ПМТФ. 2017. – Т. 58, № 6. – С. 167–176.
5. Терентьев А. Г. К линейной теории кавитационного обтекания препятствий / А. Г. Терентьев // Сборник научных трудов «Вопр. прикл. матем. и мех.». Чебоксары: изд-во Чуваш. ун-та. – 1971. – Вып.1. – С. 3–35.
6. Гуревич М. И. Теория струй идеальной жидкости / М. И. Гуревич. – М. Наука. – 1979. – 536 с.
7. Полубаринова-Кочина П. Я. Нестационарное движение в теории фильтрации / П. Я. Полубаринова-Кочина // Прикл. математика и механика. – – Т. 9. – С. 79-90.
8. Галин Л. А. Нестационарная фильтрация со свободными границами / Л. А. Галин. // Докл. АН СССР. – – Т. 47. – С. 246-249.
9. Житников В. П. Методы верификации математических моделей в условиях неопределенности / В. П. Житников, Н. М. Шерыхалина // Вестник УГАТУ. – – № 2. – С. 53–60.
10. Шерыхалина Н.М. Методы обработки результатов численного эксперимента для увеличения их точности и надежности / Н. М. Шерыхалина // Вестник УГАТУ. – – Т. 9. – №2 (20). – С. 127–137.

Список литературы на английском языке / References in English

1. Howison S. D. Complex variable methods in Hele Shaw moving boundary problems / S. D. Howison // Eur. J. Appl. Math. – 1992, Vol. 3. – P. 209-
2. Polubariniva-Kochina P. Ya. Teoriya dvizheniya gruntovyh vod [Theory of Groundwater Movement] 2nd edition / P. Ya. Polubariniva-Kochina // Princeton: Princeton Univ. Press. – 1962. – 350 p.
3. Ockendon J. R. Kochina and Hele-Shaw in modern mathematics, natural sciences, and technology / J. R. Ockendon, S. D. Howison // J. Appl. Math. Mech. 2002. – Vol. 66. – No. 3. – P. 505–512.
4. Zhitnikov V. P. Modelirovanie elektrokhemicheskogo kopirovaniya v yacheyke konechnoy shiriny [Modeling of electrochemical copying in a finite-width cell] / V. P. Zhitnikov, N. M. Sherykhalina, A. A. Zaripov // Journal of Applied Mechanics and Technical Physics. – 2017. – Vol. 58. – No. 6. P. 1099–1107.
5. Terentiev A. G. K lineynoy teorii kavitatsionnogo obyekaniya prepyatstviy [On the linear theory of cavitating flows about obstacles] / A. G. Terentiev // Sbornik nauchnyh trudov “Voprosy prikladnoy matematiki i mekhaniki” [Collection of scientific works “Problems of applied Mathematics and mechaniks”] – 1971. – Vol. 1. – Cheboksary: Chuvash University. – P. 3–35. [in Russian]
6. M. I. Teoriya struy ideal’noy zhidkosti [Theory of flows of ideal fluid] / M. I. Gurevitch. – Moscow: Nauka. – 1979. – 536 p. [in Russian]
7. Polubariniva-Kochina P. Ya. Nestatsionarnoye dvizhenie v teorii fil’tratsii [Non-stationary motion in the filtration theory] // Prikladnaya matematika i mekhanika [Applied mathematics and mechanics]. – – Vol. 9. P. 7990. [in Russian]
8. Galin L. A. Nestatsionarnaya fil’tratsiya so svobodnymi granitsami [Non-stationary filtration with free boundaries] / L. A. Galin // Doklady AN SSSR [Reports of Acad. of Sci., USSR]. – – Vol. 47. – P. 246-249. [in Russian]
9. Zhitnikov V. P. Metody verifikatsii matematicheskikh modeley v usloviyakh neopredelennosti Методы верификации математических моделей в условиях неопределенности [Methods of verification of mathematical models in conditions of inconfidence] / V. P. Zhitnikov, N. M. Sherykhalina // Vestnik UGATU [Bulletin of Ufa Aviation Techn. Univ.] – – No. 2. – P. 53–60. [in Russian]
10. Sherykhalina N. M. Metody obrabotki rezul’tatov chislennogo eksperimenta dlya uvelicheniya ikh tochnosti I nadezhnosti [Methods of processing of numerical experiment results for its accuracy and reliability increase] // Vestnik UGATU [Bulletin of Ufa Aviation Techn. Univ.] – – Vol. 9, – No.2 (20). P. 127-137. [in Russian]