ВОССТАНОВЛЕНИЕ ФОНОННОГО СПЕКТРА ПО ДАННЫМ ТЕПЛОЕМКОСТИ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ

Волкова В.К.¹, Сулейменова Д.А.², Афоничев Н.Ю.³

¹ORCID: 0000-0002-8166-9114, кандидат технических наук, доцент, ²ORCID: 0000-0003-4909-8806, студент, Омский государственный технический университет, ³ORCID: 0000-0002-7258-6165, старший преподаватель, Омский государственный университет путей сообщения

ВОССТАНОВЛЕНИЕ ФОНОННОГО СПЕКТРА ПО ДАННЫМ ТЕПЛОЕМКОСТИ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ

Аннотация

В статье предложен численный метод определения плотности фононных состояний композиционных материалов по экспериментальным данным теплоемкости композитных материалов на основе политетрафторэтиленовой матрицы (ПТФЭ). Проанализированы максимальные и граничные значения интенсивности фононных спектров в зависимости от структуры макромолекул «матрица+наполнитель». Результаты, полученные с помощью вычислений, находятся в хорошем согласии с экспериментально определёнными фононными спектрами для ряда исследованных композитов с наполнителем из углеродного волокна.

Ключевые слова: фононный спектр, теплоемкость, полимер, композит, матрица.

Volkova V.K.¹, Suleymenova D.A.², Afonichev N.Yu.³

¹ORCID: 0000-0002-8166-9114, PhD in Engineering Science, Associate Professor, ²ORCID: 0000-0003-4909-8806, Student, Omsk State Technical University, ³ORCID: 0000-0002-7258-6165, Senior Lecturer, Omsk State Transport University

THE CREATION OF THE PHONON SPECTRUM ACCORDING TO THE SPECIFIC HEAT FOR COMPOSITE MATERIALS

Abstract

The paper proposed a numerical method for determining the phonon density of States of the composite materials according to the experimental data of the heat capacity of composite materials based on polytetrafluoroethylene matrix (PTFE). The maximum boundary values were analyzed and phonon spectra intensity depending on the structure of macromolecules "matrix + filler". The results obtained by calculations are in good agreement with the experimentally determined phonon spectra for a number of the studied composites filled with carbon fiber.

Keywords: phonon spectrum, heat capacity, polymer, composite, matrix.

 Introduction

Wide application of composite materials on polymer base in the industry (for example, non-lubricated friction units of machines) determines the relevance of the creation of their new version. Composite materials based on PTFE possess the most universal properties, maintaining performance in a wide range of temperatures from cryogenic 10-20 K to 450 K.

The behavior of thermodynamic and other macroscopic parameters of a substance is mainly determined by its macroscopic characteristics. However, the complexity and diversity of this relationship requires further a deeper understanding of macro – and micro characteristics of substances derived from the experiment. One of the main experimentally determined quantities is the heat capacity. The study of this quantity allows obtaining qualitative and quantitative information about any thermodynamic processes occurring in a particular system, and the temperature dependence of the specific heat with high accuracy to determine its thermodynamic functions. Analysis of the temperature dependence of heat capacity of polymers allows obtaining important information about the nature of the polymers and methods of the theoretical description of this class of substances. For the solution of material science tasks of predicting properties of composite materials is the search of methods of restoration of the phonon spectrum on the data on heat capacity.

For information about the phonon spectrum and the spectral phonon density of States, along with purely experimental methods, there are methods that use computational methods based on the different measured spectral characteristics, the data on elastic modulus, sound velocity, etc. Methods of determining the spectral density for the crystal structures are described in current literature [1, P.3]. But there is no common method of solving this problem for polymer composites. Phonon plays essential roles in dynamical behaviors and thermal properties, which are central topics in fundamental issues of materials science. In this article we propose a method based on the numerical solution of the problem for the polymer composite with filler.

Attempts to determine the energy spectrum of the Bose-Einstein condensate system by its heat capacity showed that the exact solution Fredholm integral of the first kind is unstable [2, P.226]. However, the solution is stable in the form of a smooth curve (envelope), which describes the spectral fine structure. A solution to this problem requires the use of special regularization techniques. The use of the operators when selecting Tikhonov regularization [3, P. 128] parameters according to the principle of the generalized discrepancy information provides detection of phonon density of states. This method makes it possible to detect the basic features of the decision function of phonon density of states.

In this contribution we present several findings concerning the modeling of creation phonon spectrum by heat capacity for composite materials.

Material and method

The present inventors made investigations of composites based on a matrix of polytetrafluoroethylene (PTFE) and carbon fiber filler (CF) The study was conducted in two stages. In the first place, inverse problem was solved "heat capacity-phonon spectrum", then took study by direct problem where the computed spectrum data on the heat capacity of the composites were obtained.

For the determination of the phonon spectrum was created by the program implementing Tikhonov regularization method decision Fredholm integral equation of the first kind:

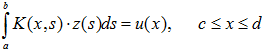
The task of the first type Fredholm equation is represented by the formula:

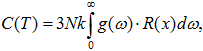
where – the function of phonon density of states, N is the number of atoms, k, h – the Boltzmann and the Planck constant respectively.

Experimentally determined heat capacity at constant pressure (C_p), to calculate the phonon spectra was excluded from C_p that portion, the anharmonicity of vibrations associated with oscillatory spectrum.

Results and discussion

Results of the first run of calculations for the determination of the phonon spectrum for the composite 6CF are presented in Fig.1. The temperature range was from 10 to 250 K. Frequency range is from 0.03 to 55 meV (in energy representation).

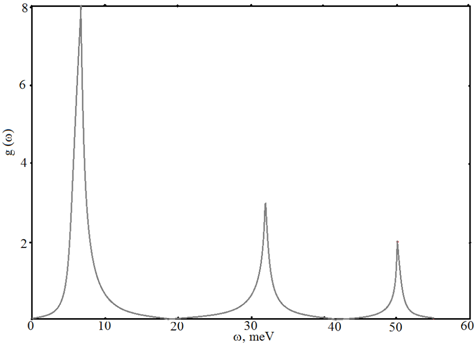
Fig. 1 – Results of the first run of calculations for the composite 6CF

 

From these results it can be concluded that the phonon spectra have studied materials as general properties and purely individual. The following can be referred to the general. The phonon spectra are expressed in three peaks values separated from each other. The estimated character not calculations makes it possible to recover the fine structure of each peak, however, from a general considerations, it can be assumed that the first peak corresponds to the longitudinal vibrations, second and third  can be segmental oscillations transverse oscillations in the macromolecules, and hence respective standing waves. The strongest peak value of density of states depends on the content of carbon fiber in the sample.

Table 1 shows the boundary frequency value w for each peak and g(w_i) corresponding to each maximum density of states. The value of w_i, standing in parentheses represents the frequency at which the maximum density of states must be. The results of the comparisons are shown in table 1, boundary strongest peak value w₁ state density depends on the content of carbon fiber in the sample (w₁ increases with increasing filler concentration) while neither the value g_max, nor its corresponding frequency w₁ for PTFE composites and practically not changed. Apparently, the low frequency peak is mainly determined by the longitudinal vibrations in the macromolecule matrix. The analysis of the results for the "average" peak g(w) indicates that a limit value is practically little depends on the concentration of the filler in the composite, exception is industrial composite КVN-3 which lacks the carbon fiber. The value of g_max(w₂) initially increased with increasing filler from 2.4 (J^.kg)^-1 for PTFE to 2.9 (J^.kg)^-1 for 6CF КVN-3, K-2, K-3, and then slightly reduced (up to 2.1 (J^.kg)^-1 for 10CF)

Table 1 – The values of the boundary frequencies w and the maxima of the state density g_max (w) for the compounds studied

	PTFE	6CF	10CF	CF	КVN-3	К-2	К-3
w1, meV	13,7	18,3	20,6	20.6	16,0	16,0	16,0
gmax (w1)	8(6,8)	8(6,8)	8,1(6,8)	8,6(9,1)	9(6,8)	8,2(6,8)	8(6,8)
w2, meV	39	41	41	41	34	39	39
gmax (w2)	2,4(30)	2,9(32)	2,1(34)	2,2(34)	2,9(25)	2,9(32)	2,8(30)
w3, meV	55	55	55	55	55	55	55
gmax (w3)	2,6(50)	2(50)	2,3(48)	1,45(48)	2,5(46)	2,4(50)	1,9(48)

The relationship of heat capacity jump from the filler’s volume fraction confirms the effect of the nature of the features of the filler on the polymer structure and molecular mobility. Using these results, the thickness of the boundary layers is calculated for each of the fillers. The small thickness of the boundary layers occur when the energy of the adhesive interaction could be compared with the energy of cohesion, and therefore the effect of solid particle surface does not extend over large distances. The formation of boundary layers of greater thickness can be explained by peculiarity of structure formation of polymer in the presence of the solid surface of the filler. For pure carbon fiber "average" peak substantially little differs from zero, apparently due to the lack of lateral segments in the macromolecule. Therefore, it is believed that the presence of this peak segmental due to vibrations.

Finally, consider the most high frequency peak g(w). It may be noted that the largest g_max for PTFE and carbon fiber for the smallest. The w₃ varies little from sample to sample. Based on the characteristic peak for this frequency range g(w) in this region is associated with the lateral oscillations in the macromolecules.

Conclusion

After the creation of phonon spectra for polytetrafluoroethylene matrix (PTFE) and carbon fiber filler (CF) was performed to calculate the heat capacity of the composite materials, a series of PTFE-CF. For this purpose, the spectra of PTFE and CF additive was applied in accordance with a volume content proportion of the filler and the polymer matrix in the composite. The results of the calculations showed good agreement with the experimental data on the heat capacity [4, P.47]. It is possible to offer the method for solving problems of determining the thermal properties of composite materials according to the known values of the heat capacity of the matrix and filler. As a result, substantially reduced time, energy and labor costs for the production of materials with desired properties.

Список литературы / References

1. Togo A. First principles phonon calculations in materials science / A. Togo, I. Tanaka // Scripta Materialia. – 2015. – Vol.108. – P. 1-5.
2. Wunderlich B. The computation of heat capacities of solid high рolimers from vibrational spectra / B.Wunderlich, H.Bu. // Thermochimacta. – 1987. – V.119. – N.1.– P. 225-230.
3. Тихонов А.Н. Методы решения некорректных задач / А.Н. Тихонов, В.Я. Арсенин // М.:Наука, 1986. – 288 с.
4. Волкова В.К. Теплофизические свойства композиционных материалов с полимерной матрицей и твердых растворов / В.К.Волкова // М.:Наука образования, 2011. – 104 с.

Список литературы на английском языке / References in English

1. Togo A. First principles phonon calculations in materials science / A. Togo, I. Tanaka // Scripta Materialia. – 2015. – Vol.108. – P. 1-5.
2. Wunderlich B. The computation of heat capacities of solid high рolimers from vibrational spectra / B.Wunderlich, H.Bu. // Thermochimacta. – 1987. – V.119. – N.1.– P. 225-230.
3. Tikhonov A.N. Metodi resheniya nekorrektnih zadach [Methods for solving the problems of incorrect] / A.N. Tikhonov, V. Ya. Arsenin // M.: Nauka [Science], 1986. – 288 p. [in Russian]
4. Volkova V.K. Teplofizicheskie svoistva kompozitsionnykh materialov s polimernoi matritsei i tverdykh rastvorov [Heat and Physical Properties of Composition Materials with Polymer Matrix and Solid Solutions] / V. K. Volkova // M.: Nauka Obrazovaniya [Science of education], 2011. – 104 p. [in Russian]