РАЗРАБОТКА МЕТОДА ОПИСАНИЯ ЗАДЕРЖЕК СТАНДАРТНЫХ ЯЧЕЕК В ЦИФРОВЫХ ИНТЕГРАЛЬНЫХ СХЕМАХ

Геворгян А.М.¹, Оганесян О.Э.², Ахвердян Т.А.³

¹Аспирант, Национальный исследовательский университет, «Московский институт электронной техники», ²Аспирант, Московский технологический университет МИРЭА, ³Аспирант, Ереванский государственный университет

РАЗРАБОТКА МЕТОДА ОПИСАНИЯ ЗАДЕРЖЕК СТАНДАРТНЫХ ЯЧЕЕК В ЦИФРОВЫХ ИНТЕГРАЛЬНЫХ СХЕМАХ

Аннотация

В статье предлагается новый подход расчета временных верификаций для библиотек стандартных ячеек, который основан на средствах схемотехнического моделирования и учитывает межсхемные и внутрисхемные технологические отклонения необходимые для статистического статического временного анализа. При допустимом быстродействии и точности, метод обеспечивает совместимость с нелинейными моделями задержек. В отличие от статистического статического временного анализа не является итерационного типа и делается только один раз для данного технологического процесса.

Ключевые слова: временная верификация, технологические отклонения, нелинейные модели задержек.

Gevorgian A.M.¹, Oganesian O.E.², Akhverdian T.A.³

¹Postgraduate student, National Research University of Electronic Technology, “Moscow Institute of Electronic Technology”, ²Postgraduate student, Moscow Technological University MIREA, ³Postgraduate student, Yerevan State University

DEVELOPMENT OF THE DESCRIPTION METHOD OF DELAYS OF STANDARD CELLS IN DIGITAL INTEGRATED SCHEMES

Abstract

The article proposes a new approach for calculating temporal verification for standard cell libraries based on circuit simulation tools with regard to inter-circuit and in-circuit technological deviations necessary for statistical static time analysis. With acceptable speed and accuracy, the method ensures the compatibility with non-linear delay models. Unlike statistical static time analysis, it is not an iterative type and is performed only once for a given technological process.

Keywords: time verification, technological deviations, non-linear models of delays.

Параллельно с  уменьшением размеров транзисторов в сверхбольших интегральных схемах уменьшается управляемость технологических процессов, что влечет за собой увеличение влияния технологических отклонений (ТО) на параметры интегральных схем (ИС) [1, С. 338]. Временной анализ при помощи имеющихся методов не дает полного представления о реальной работе и о реальных параметрах цифровых ИС. Выполнение временного анализа на граничных случаях [2, С. 91] уже не достаточно, поскольку в субмикронных технологиях отклонения физических параметров ИС больше не являются монотонными функциями [1, С. 340],[3, С. 330]. Поэтому нужно выполнять проверки для нескольких десятков случаев, что требует очень больших машинных и человеческих ресурсов. В то же время введение коэффициента отклонения для ТО [2, С. 91] и умножение на этот коэффициент задержки схемы в субмикронных технологиях приводит к пессимистичным оценкам [2, С. 91-93],[4],[5, С. 321] и усложняет соблюдение временных параметров с техническим заданием. Даже если удается получить параметры, удовлетворяющие техническому заданию, то усложняется структура схемы, а количество элементов увеличивается, что становится причиной увеличения площади схемы, что также приводит к уменьшению рабочей частоты. В таких условиях есть крайняя необходимость в созданий новых методов средство автоматического временного анализа, которые позволили бы учитывать особенности субмикронных технологий и предоставит разработчику необходимые данные о временных параметрах в цифровых ИС. Это даст возможность во время временного анализа в цифровых ИС получить результаты, более близкие к реальности по сравнению с известными методами и средствами.

Описания стандартных ячеек при использовании традиционного статического временного анализа (СВА) в основном реализуется при помощи нелинейных моделей задержек. Но если нелинейные модели задержек содержат временную информацию для ячейки (в зависимости от входного фронта и от выходной емкости), то для проведения статистической проверки нужны модели, которые будут содержать временную информацию, которая зависит не только от выходной емкости ячейки и от входного фронта, но и от некоторых технологических параметров, как показано на рис. 1. Важно отметить, что модель статистической задержки должна учитывать как внутрисхемные (ВС), так и межсхемные (МС) отклонения. Для статистического описания используется программа Liberty-NCX [6], при помощи которого можно получить как единый файл описания, так и отдельные файлы для каждого технологического параметра для ВС и МС отклонений.

Создание модели МС отклонений для параметров A и B позволит получить информацию о величине ряда важных временных параметрах, таких, как задержка, наклон выходного сигнала, время установки и удержания.

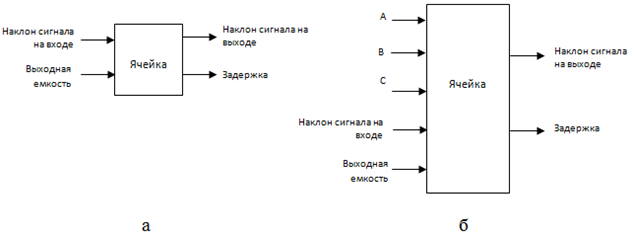
Рис. 1 - Общий вид описания ячейки при использовании СВА (а) и ССВА (б) методов

 

Ясно, что если для двух параметров выбрать их номинальные значения, которые будут изменяться в допустимом интервале для каждого из них, то получится определенная функциональная зависимость выходного временного параметра ячейки от изменений A или B параметров, как показано на рис. 2. Для создания модели сначала данная ячейка моделируется для номинальных значений A и B параметров. Номинальные значения для приведенных выше кривых зависимостей показаны на рис. 3. Для каждой точки на кривой, которое представляет из себя значение параметра, соответствует коллекция состоящей из всех параметров для данного значения. После моделирования для номинальных значений, задержка ячейки считается также еще в дополнительных двух точках, которые находятся в разных сторонах номинального значения.

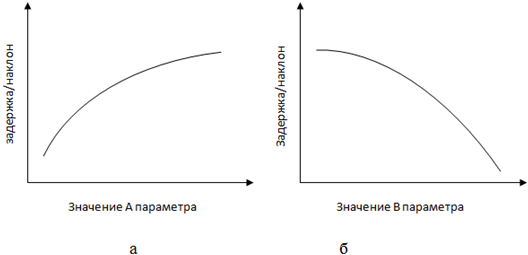
Рис. 2 - Зависимость выходной задержки ячейки от A(а) и B(б) параметров

 

Для нахождения задержек в этих точках, значения остальных параметров остаются равны их номинальным,  меняется только значение для наблюдаемого параметра. Это позволит определить изменения значения задержки в зависимости от отклонения только данного параметра.

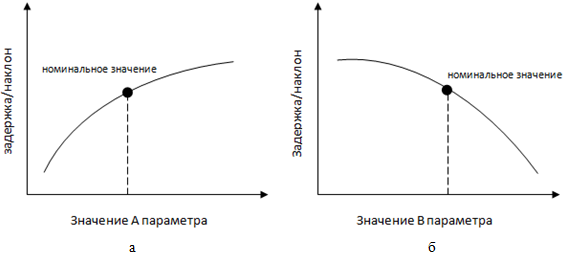
Рис. 3 - Зависимость выходной задержки ячейки от номинальных значений A(а) и B(б) параметров

Вследствие МС отклонений для меняющихся N количества параметров нужно будет 2N+1 описаний – два описания для не номинальных значений и одно для общего описания номинальных значений. В случае двух параметров для МС отклонений описание будет иметь вид, приведенный на рис. 4

После рассмотрения влияния каждого отдельного параметра, необходимо получить общее отклонение задержки, если несколько параметров меняются одновременно. Поскольку эти параметры не зависят друг от друга, то для расчета их одновременных влияний можно использовать принцип суперпозиции. Для этого необходимо суммировать задержки всех параметров влияющих на отклонения.

Рис. 4 - Описания N размерное пространство A и B параметров в случае МС отклонений

 

Кроме расчета МС ТО необходимо создать модель, которая будет содержать информацию и о ВС отклонениях. Но в отличие от МС отклонений (рис. 5а), ВС отклонения меняются по – своему (рис. 5б) для каждого параметра транзистора, следовательно, расчет при помощи предложенного выше метода не эффективен.

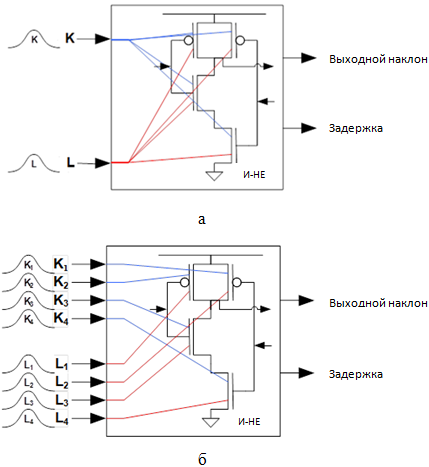
Рис. 5 – Влияния МС (а) и ВС (б) отклонений на “И-НЕ” стандартную ячейку

 

Вследствие этого во временных моделях ячеек будут содержаться зависимости выходных задержек от всех параметров всех транзисторов. Получение такого вида зависимости требует машинных, человеческих и временных больших затрат и на практике не применяем. Поэтому необходим другой метод для проверки временных параметров ВС отклонений. На рис.6 показан предложенный метод моделирования ВС отклонений.

В [7]-ом показано, что если в цифровой схеме все параметры каждого транзистора меняются нормальным распределением вне зависимости от других, то выходная задержка и наклон сигнала схемы также будут иметь нормальное распределение.

Предлагается при помощи средства схемотехнического моделирования сделать моделирование Монте-Карло, для нахождения значений выходной задержки и наклона ячейки.

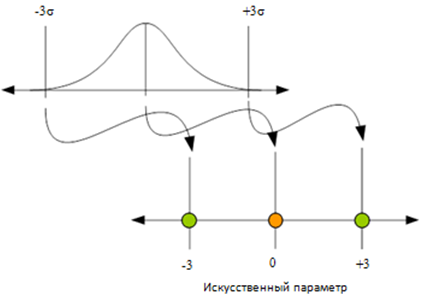
Рис. 6 - Создание искусственного параметра для моделирования ВС разбросов

 

После этого, имея значения среднего, а также +3σ и -3σ распределений,  приписать их к новой искусственной переменной, чьи +3σ и -3σ значения будут соответствовать на выходе схемы +3σ и -3σ отклонений и полученному среднему значению распределения Гаусса. Это позволит посчитать все влияния ВС отклонений при помощи одной переменной.

В таблице показаны сравнения для двухвходовых “И”, “ИЛИ-НЕ” ячеек, а также для инвертора, буфера и последовательно соединенных пяти инверторов.

 

Таблица 1 – Сравнение точности методов описания стандартных ячеек

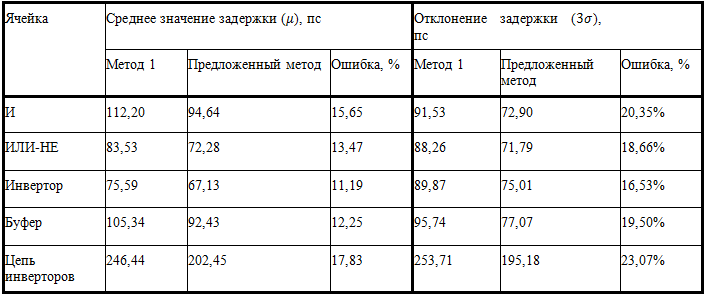
Как можно увидеть (табл. 1), разница точности между существующим и предложенным методами для среднего значения задержки варьируется в границах 11%-18%, а для  отклонения - в границах 16%-23%.   В [8]-ом такие же отличия были при сравнении предложенного метода и метода Монте-Карло. С другой стороны, описания при помощи [8] метода занимает в 1.5 раза меньше времени, чем предложенный метод. Но полученные характеристики в [8]-ом методе своим форматом несовместимы с моделями нелинейных задержек. Важно также отметить, что, в отличие от ССВА, предложенный метод не итерационного типа и делается один раз для данной технологии.

Список литературы / References

1. Parameter variations and impact on circuits and microarchitecture / S. Borkar, T. Karnik, S. Narendra et al // 40^th Design Automation Conference. - Anaheim, 2003. - P. 338-342.
2. Forzan C., Pandini D. Why We Need Statistical Static Timing Analysis // IEEE International Conference on Computer Design. - Lake Tahoe, 2007. - P. 91-96.
3. Orshansky M., Nassif S. Design for Manufacturability and Statistical Design. - Springer, 2007. - 330 p.
4. Sapatnekar S. Timing. - Springer, 2004. - 910 p.
5. Gupta P., Heng F.-L. Toward a systematic-variation aware timing methodology // 41^th Design Automation Conference. - San Diego, 2004. - P. 321-326.
6. Liberty NCX: The Fastest Path to Production Current-Source Libraries // www.synopsys.com
7. Petrosyan G.A. A Method of Logic Level Statistical Static Timing Analysis // Proceedings of the 8^th International Conference on Semiconductor Micro- and Nanoelectronics. - Yerevan, 2011. - P. 263-266.
8. Aftabjahani S.-A. Compact Variation-Aware Standard Cell Models for Statistical Static Timing Analysis:  Ph.D. dissertation / Georgia Institute of Technology. - Atlanta, 2011. - 214 p.