ПРИНЦИП РАВНОПРОЧНОСТИ В ПРИНЯТИИ РЕШЕНИЙ

Кумунжиев К.В.¹, Головин В.А.²

¹Доктор технических наук, Ульяновский государственный университет, ²Кандидат технических наук, Ульяновский государственный университет

ПРИНЦИП РАВНОПРОЧНОСТИ В ПРИНЯТИИ РЕШЕНИЙ

Аннотация

Термин «принятие решений» можно трактовать как в широком, так и в узком смысле.  В первом случае речь идет об объединении, по крайней мере,  двух процедур: анализа вариантов и выбора предпочтительного. В данной статье мы будем говорить преимущественно о процедуре  выбора предпочтительного варианта. Развиваются две теории принятия решений –психологическая и рациональная. Первая – это система наблюдений и утверждений о том, как люди в действительности принимают решения, и какие ошибки при этом совершают. Вторая создавалась математиками и экономистами и говорит, как надо принимать решения, чтобы выбрать наилучший вариант.

Ключевые слова: принятие решений, оптимизация, поверхность Парето.

Kumunzhiev K.V.¹, Golovin V.A.²

¹PhD in Engineering, Ulyanovsk State University, ²PhD in Engineering, Ulyanovsk State University

PRINCIPLE OF STRENGTH BALANCE IN DECISION-MAKING

Abstract

The term "decision-making" can be interpreted both in broad and in a narrow sense. In the first case, it involves combination of at least two procedures: analysis of options and selection of the preferred one. In this paper we mainly talk about the procedure of the preferred option selection. Two theories of decision-making are considered: psychological and rational one. The first is a system of observations and statements about how people actually make decisions, and what mistakes they make. The second was created by mathematicians and economists and shows how to make decisions in order to choose the best option.

Keywords: decision making, optimization, Pareto surface.

В соответствии с общей схемой проектирования к моменту необходимости принятия решения мы имеем ряд альтернатив, для которых определен набор показателей качества, шкалы, по которым они будут измеряться, и оценки показателей. Наша задача - найти наилучший вариант.

Говоря о различных альтернативах, мы, прежде всего, имеем в виду   различные структуры. Но свойства любой системы зависят от параметров и структуры. Поэтому имеет смысл сравнивать структуры лишь после того, как для каждой из них найдены наилучшие параметры. Поэтому зафиксируем следующее. Задача выбора решается на двух уровнях: на уровне параметров и на уровне структуры.

Определяются возможные варианты достижения цели – структуры. Для каждой структуры  тем или иным способом ищутся наилучшие значения параметров. Далее находятся показатели качества для каждой структуры при наилучших (оптимальных) значениях параметров. И только после этого возможно обоснованное сравнение различных структур и выбор наилучшей. Конечно, такая схема представляется достаточно трудоемкой, однако только так можно выбрать действительно лучший вариант.

При определении требований к показателям качества стоит отметить, что они могут быть формализованы в одной из трех форм

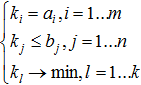
В случае, если требуется найти экстремум одного показателя качества, задача легко преобразуется в задачу математического программирования:

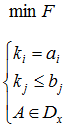
где  - критерий оптимизации.

Первая и основная проблема возникает, когда число показателей, для которых требуется обеспечить  экстремум, больше единицы, т.е. когда приходят решать задачу векторной оптимизации. В этом случае, тем или иным путем, мы должны перейти от вектора показателей качества к единому критерию оптимизации. Существует ряд методов решения этой задачи.

Поиск безусловно лучших решений. Центральным понятием этого метода является поверхность Парето. Пространство параметров отображается в пространство показателей качества: переход от одной точки к другой в пространстве параметров смещает отображающую точку в пространстве показателей. На каких-то этапах можно производить изменение параметров таким образом, что удается улучшать одни показатели без ухудшения других. Однако неизбежно наступает ситуация, когда нельзя улучшать одни показатели без ухудшения других. Множество таких точек образует в многомерном пространстве показателей качества поверхность, которую и называют поверхностью Парето. Поэтому основное требование к любому решению – оно должно принадлежать поверхности Парето. Решения, лежащие на поверхности Парето, и называют безусловно лучшими. Выявить поверхность Парето можно, решая многократно задачу оптимизации по критерию. Решение такой задачи достаточно трудоемко и не является окончательным.

Метод ранжирования показателей качества (метод уступок). Все показатели ранжируются по значимости: k₁, k₂,...k_n. Затем решается оптимизационная задача с критерием F=k₁. Логика следующего шага такова: давайте немного ухудшим значение показателя k₁ и за счет этого улучшим показатель k₂. При этом показатель k₁ переводится в разряд ограничений с коэффициентом, отражающим его допустимое ухудшение. Задача выглядит так:

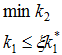
где  - оптимальное значение, найденное на предыдущем шаге, ξ - весовой коэффициент. Далее процесс повторяется по отношению к последующим показателям.

Свертка показателей качества. Свертка предполагает использование в качестве критерия оптимизации функции от показателей качества с некоторыми весовыми коэффициентами. Здесь сохраняется проблема выбора весовых коэффициентов. Более того, весовые коэффициенты должны учитывать как значимость показателей, так и интервал их изменения. Это затрудняет использование свертки.

Оптимизация относительно идеальной точки. Упростить ситуацию с выбором весовых коэффициентов может введение идеальной точки. Идеальная точка – набор значений показателей качества, идеальных с точки зрения проектировщика. Использование идеальной точки в значительной мере снимает проблему, связанную с необходимостью учесть при выборе весовых коэффициентов интервалы их значений, но в целом вопрос остается открытым.

Использование принципа равнопрочности (ПР). Описанные выше способы перехода от вектора показателей качества к единому критерию оптимизации имеют общий недостаток: они допускают решения, лежащие на границах допустимых значений показателей качества. Дело в том, что в реальности для любого объекта задаются допустимые ограничения на показатели качества. При выполнении их цель считается достигнутой (изделие работоспособно). Выход за границы хотя бы одного показателя означает отказ изделия. Расположение решения на границе поля допуска означает большую вероятность выхода за границу поля допуска, т.е. низкую надежность изделия. Поэтому желательно, чтобы, с одной стороны, полученное решение принадлежало поверхности Парето, с другой – чтобы оно было равноудалено от границ поля допуска. Равноудаленность здесь понимается  не в прямом геометрическом смысле, а как равновероятность выхода за границы поля допуска.

Изделие, удовлетворяющее этим требованиям, принято называть равнопрочным. Оно должно быть спроектировано так, чтобы все его узлы отказывали одновременно после выработки заданного ресурса. При этом затраты оказываются минимальными.

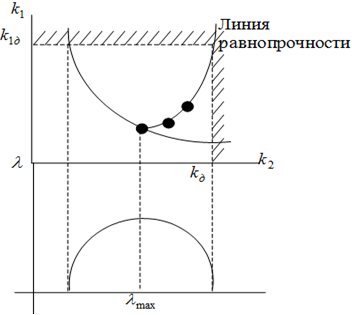
Рис.1 - Использование ПР

 

Суть метода иллюстрирует рис.1. Верхний рисунок – линия Парето для двухмерного случая,   - допустимые значения показателей качества. Нижняя часть рисунка – зависимость вероятности безотказной работы λ от выбора параметров и, соответственно, положения отображающей точки на плоскости показателей качества. Следовательно, процесс оптимизации должен строиться таким образом, чтобы, с одной стороны, вывести решение на линию Парето, с другой – двигаться по линии равнопрочности, точки которой равноудалены от границ поля допуска. При этом мы неизбежно выйдем на линию Парето и в точку, наиболее удаленную, в определенном смысле, от границ поля допуска.

Математическая формулировка задачи выглядит следующим образом:

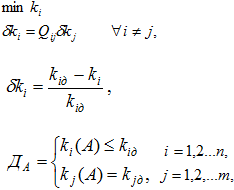
где Д_А - область допустимых значений показателей качества. Иными словами, необходимо провести оптимизацию по любому из показателей качества, введя при этом дополнительные ограничения в виде равенств. Q_ij - функции равнопрочности.

Функции равнопрочности задают линию в пространстве качеств, двигаясь по которой в процессе оптимизации по одному (любому) показателю качества, мы обязательно выйдем на поверхность Парето.

Вид функции равнопрочности определяется условиями задачи. Так, если априорная информация отсутствует, то можно взять ее в виде отношения допустимых значений

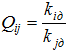
где  - допустимые значения показателей качества. Если определяющими являются случайные  отклонения, то рекомендуется функция равнопрочности в виде:

где  - среднеквадратическое отклонение.

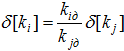
Для случая, когда определяющим является временной дрейф параметров, рекомендуется функция равнопрочности в виде

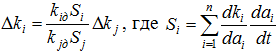
• скорость дрейфа показателя качества, выраженная через дрейф параметров. Возможны ограничения и в другой форме.

Использование принципа равнопрочности позволяет найти решение, оптимальное по Парето, и наилучшим образом использовать потенциальные возможности структуры.

Список литературы / References

1. Кумунжиев К. В. Проектирование систем: изобретательство, анализ, принятие решений: учебное пособие / К. В. Кумунжиев. –Ульяновск: УлГТУ, 2009. – С. 183.
2. Ларичев О. И. Теория и методы принятия решений, а Также Хроника событий в Волшебных Странах: Учебник / О.И. Ларичев. - М.: Логос, 2000. - 296 с.

Список литературы на английском языке / References in English

1. Kumunzhiev K. V. Proektirovanie system: izobretatelstvo, analiz, prinyatie resheniy: uchebnoe posobie [Design of systems: invention, analysis, decision-making: manual]/ K. V. Kumunzhiev. – Ulyanovsk: UlGTU, 2009. P. 183.
2. Larichev O. I. Teoriya I metodi prinyatiya resheniy [The theory and methods of decision-making, and also Chronicle of events in the Magic Countries: Textbook]/ O. I. Larichev. –M.:Logos, 2000. –P. 296.