КОРРЕКТНОСТЬ ВОССТАНОВЛЕНИЯ МАССОВЫХ ПАРАМЕТРОВ РАКЕТНОГО ДВИГАТЕЛЯ ТВЕРДОГО ТОПЛИВА
Сафина Г.Ф.
ORCID: 0000-0002-7326-0896, Кандидат физико-математических наук, Нефтекамский филиал Башкирского государственного университета
КОРРЕКТНОСТЬ ВОССТАНОВЛЕНИЯ МАССОВЫХ ПАРАМЕТРОВ РАКЕТНОГО ДВИГАТЕЛЯ ТВЕРДОГО ТОПЛИВА
Аннотация
Рассмотрена обратная задача диагностирования параметров ракетного двигателя твердого топлива по известным значениям частот его малых свободных колебаний. Показана корректность по А.Н. Тихонову обратной задачи восстановления массовых параметров пружинно-массовой модели РДТТ. Сформулирована и доказана соответствующая теорема. Найден алгоритм решения задачи, подтверждающий единственность восстановления параметров по известным значениям четырех частот колебаний ракетного двигателя. Алгоритм решения подтвержден на конкретном примере.
Ключевые слова: частоты колебаний, множество корректности, диагностирование параметров.
Safina G.F.
ORCID: 0000-0002-7326-0896, PhD in Physics and Mathematics, Neftekamsk Branch of Bashkir State University
CORRECTNESS OF RESTORATION OF MASS PARAMETERS OF ROCKET ENGINE OF SOLID FUEL
Abstract
The article considers inverse problem of diagnosing the parameters of a rocket engine solid fuel according to known values of the frequencies of small free oscillations. The correctness is shown according to A.N. Tikhonov's inverse problem of restoring mass parameters of the spring-mass model of a solid propellant rocket. The corresponding theorem is formulated and proved. An algorithm for solving the problem is found. It confirms the uniqueness of the parameters reconstruction from the known values of the four frequencies of the rocket engine oscillations. The decision algorithm is confirmed by a concrete example.
Keywords: oscillations frequency, correctness set, parameters diagnostics.
Приведем краткие сведения по свободным колебаниям ракетного двигателя твердого топлива [1]-[3]. Описание расчетной схемы РДТТ, включающей в себя снаряженный корпус двигателя, сопловое днище и продукты сгорания, привело к рассмотрению упруго-массовой модели (рисунок 1).
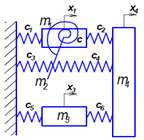
Рис. 1 – Упруго-массовая модель РДТТ
Модель учитывает как массовые параметры конструкции (корпуса m1, заряда твердого топлива m2, продуктов сгорания m3, сопла m4), так и упругие характеристики (жесткость оболочки c1, жесткость газа в зазорах между зарядом твердого топлива и днищами двигателя c2, жесткость газа в свободном объеме c3 и жесткость наполнителя cN) и перемещения соответствующих элементов системы ( x1, x2, x3, x4).
Для математического описания задачи с помощью аналитического подхода к расчету свободных колебаний рассматриваемой конструкции использовались уравнения Лагранжа для механической системы с конечным числом степеней свободы. При этом с учетом того, что модель совершает малые свободные колебания в работе [1] получено следующее уравнение:
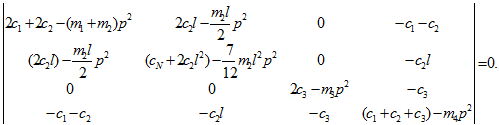 (1)
(1)
в котором p – собственная частота колебаний.
Раскрытие определителя в (1) приводит к уравнению четвертой степени относительно p2 и позволяет по известным физическим параметрам модели двигателя определять соответствующие значения частот колебаний.
В работе [2] поставлена обратная задача диагностирования массовых характеристик модели РДТТ, которая решена на примере восстановления массы корпуса и заряда твердого топлива по известным значениям трех частот колебаний. Метод сведен к решению двух нелинейных систем уравнений с последующим определением их общего решения. В работе [3] подобная задача решена для диагностирования жесткостных параметров рассматриваемой конструкции ракетного двигателя.
В продолжение исследований [2] приведем другой подход к решению обратной задачи, который ответит не только на вопрос о единственности решения обратной задачи, но и позволит определить необходимое количество частот колебаний для единственного восстановления характеристик, а также позволит показать корректность обратной задачи по А.Н. Тихонову.
Опишем данный метод. Для этого уравнение (1) приведем к виду:
![]() (2)
(2)
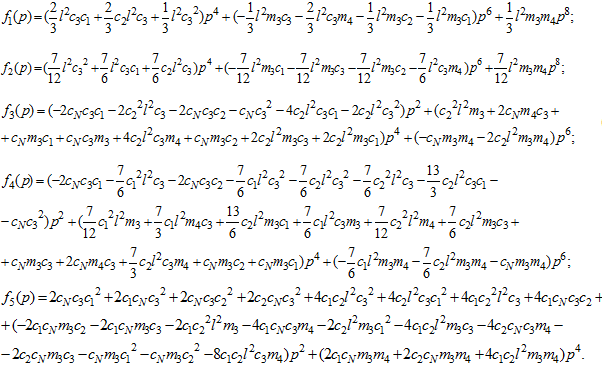
Пусть известны значения ![]() четырех частот колебаний модели РДТТ. Тогда подставляя их в частотное уравнение (2) получим:
четырех частот колебаний модели РДТТ. Тогда подставляя их в частотное уравнение (2) получим:
![]() (4)
(4)
Система (4) является системой четырех линейных уравнений от четырех неизвестных a, b, m1, m2. Найдем решение (4) по правилу Крамера. При этом имеем, что если определитель
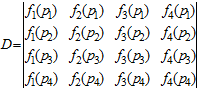 (5)
(5)
системы уравнений (4) не равен нуля, то искомые массы корпуса и заряда твердого топлива определяются однозначно по формулам:
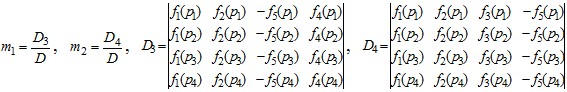 (6)
(6)
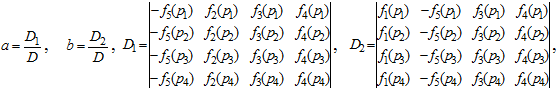 (7)
причем с учетом введенных параметров должны выполняться равенства
(7)
причем с учетом введенных параметров должны выполняться равенства
Определение частот колебаний ![]() с помощью вискозиметров чаще является приближенным, поэтому равенства (8), находимые по таким частотам могут и не выполняться. Это в свою очередь говорит о том, что система уравнений (4) может и не иметь решений, и поэтому рассматриваемая я задача может оказаться некорректной по Адамару. Тем не менее, она будет корректной по А.Н. Тихонову [4]. Покажем это.
с помощью вискозиметров чаще является приближенным, поэтому равенства (8), находимые по таким частотам могут и не выполняться. Это в свою очередь говорит о том, что система уравнений (4) может и не иметь решений, и поэтому рассматриваемая я задача может оказаться некорректной по Адамару. Тем не менее, она будет корректной по А.Н. Тихонову [4]. Покажем это.
Для этого под оператором R понимаем отображение, задаваемое системой (4), оно переводит четверку неизвестных a, b, m1, m2 в соответствующую четверку собственных частот ![]() , при этом определитель (5)
, при этом определитель (5) ![]() . Под множеством V понимаем пространство R4 элементов
. Под множеством V понимаем пространство R4 элементов ![]() с нормой
с нормой ![]() , а под z – пространство R4 элементов
, а под z – пространство R4 элементов ![]() с нормой
с нормой ![]() , при этом образ множества M при отображении с помощью оператора R есть множество Λ.
, при этом образ множества M при отображении с помощью оператора R есть множество Λ.
Тогда задача Rv=z корректна по А.Н. Тихонову, так как: 1) известно, что решение задачи существует и принадлежит некоторому множеству ![]() ; 2) решение единственно на множестве M; 3) для любого ε>0 существует такое δ>0, что для любых z и
; 2) решение единственно на множестве M; 3) для любого ε>0 существует такое δ>0, что для любых z и ![]() из Λ=RM и таких, что
из Λ=RM и таких, что ![]() следует, что
следует, что ![]() .
.
В указанном множестве корректности обратной задачи построим теперь алгоритм его решения. Так как искомые параметры a, b, m1, m2 существуют, собственные частоты ![]() и определители
и определители ![]() ,
, ![]() найдены точно, то условия (8) выполняются. Тогда искомые параметры определяются формулами (5)-(7).
найдены точно, то условия (8) выполняются. Тогда искомые параметры определяются формулами (5)-(7).
В том случае, когда частоты ![]() найдены с погрешностью
найдены с погрешностью ![]() , и определители
, и определители ![]() ,
, ![]() приближенные, то равенства (8), которые могут не выполняться, можно и не рассматривать. Действительно, в этом случае решением является следующая четверка параметров: значения m1, m2 определенные формулами (5), (6), в которых
приближенные, то равенства (8), которые могут не выполняться, можно и не рассматривать. Действительно, в этом случае решением является следующая четверка параметров: значения m1, m2 определенные формулами (5), (6), в которых ![]() , D3, D4 являются приближенными, а новые параметры a, b определим в соответствие с равенствами
, D3, D4 являются приближенными, а новые параметры a, b определим в соответствие с равенствами ![]() .
.
Найденная по такому алгоритму четверка искомых параметров будет лежать в множестве корректности по А.Н. Тихонову, так как для нее уже выполнено условие (8). Решение будет тем точнее, чем ближе к точным собственным частотам ![]() будут зафиксированные вискозиметром значения
будут зафиксированные вискозиметром значения ![]() .
.
Отметим, что по ходу определения множества корректности по А.Н. Тихонову и построения алгоритма решения рассматриваемой обратной задачи, доказана следующая теорема.
Теорема. Если известны ненулевые частоты ![]() колебаний РДТТ – корни уравнения (2), определитель (5) системы (4) также отличен от нуля, то задача восстановления массовых параметров корректна по А.Н. Тихонову, а единственное решение определяется формулами (5), (6).
колебаний РДТТ – корни уравнения (2), определитель (5) системы (4) также отличен от нуля, то задача восстановления массовых параметров корректна по А.Н. Тихонову, а единственное решение определяется формулами (5), (6).
Алгоритм решения задачи восстановления массовых параметров ракетного двигателя рассмотрим на конкретных примерах.
Пример 1. По известным частотамколебаний конструкции ракетного двигателя определить массу его корпуса и массу заряда твердого топлива, если остальные физические параметры рассматриваемой механической системы следующие:
![]() (9)
(9)
Решение. Подставим физические параметры (9) в равенства (3) определим все необходимые значения ![]() при известных частотах
при известных частотах ![]() . С помощью соответствующей программы имеем:
. С помощью соответствующей программы имеем:
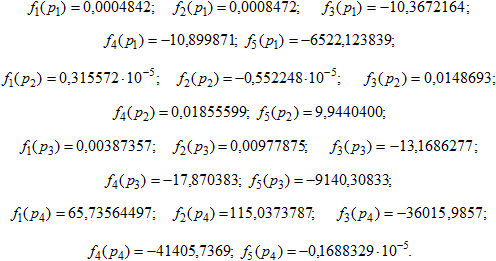
Значит, масса корпуса и масса заряда твердого топлива соответственно равны ![]() .
.
Отметим, что искомые массовые параметры определены верно. Это подтверждает решение прямой спектральной задачи, а именно, при заданных физических характеристиках (9) и массах ![]() , частотное уравнение (1) (или (4)) имеет корни:
, частотное уравнение (1) (или (4)) имеет корни:
![]()
Пример 2. Определить массу корпуса и массу заряда твердого топлива ракетного двигателя, если известны частоты
![]()
С учетом заданных частот ![]() колебаний и параметров (10) соответствующие функции равенств (3) имеют значения:
колебаний и параметров (10) соответствующие функции равенств (3) имеют значения:
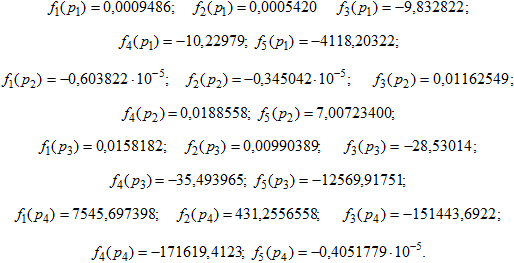
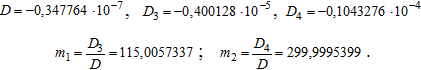 Имеем в данном следующие значения искомых массовых параметров
Имеем в данном следующие значения искомых массовых параметров
По решению прямой задачи можно снова убедиться в правильности восстановленных массовых характеристик при заданных частотах колебаний ракетного двигателя.
Таким образом, проведенные в работе исследования позволяют сделать следующие выводы: 1) рассмотрен метод введения дополнительных переменных в обратной задаче; 2) показаны единственность и корректность поставленной обратной задачи; 3) определено необходимое количество частот колебаний, позволяющее восстановить единственным образом массовые характеристики ракетного двигателя.
Список литературы / References
- Модорский В.Я. Моделирование газоупругих колебательных процессов в ракетных двигателях твердого топлива / В.Я. Модорский, А.В. Козлова // Вестник Самарского государственного технического университета. Серия: Физико-математические науки. – 2006. № 43. – С. 163-167.
- Сафина Г.Ф. Моделирование в диагностировании массовых характеристик ракетного двигателя / Г.Ф. Сафина // Актуальные вопросы в научной работе и образовательной деятельности: сборник научных трудов по материалам Международной научно-практической конференции: в 11 частях. – 2014. – С. 86-88.
- Сафина Г.Ф. Диагностирование жесткостных характеристик ракетного двигателя твердого топлива / Г.Ф. Сафина // Теоретические и прикладные вопросы науки и образования: сборник научных трудов по материалам Международной научно-практической конференции: в 16 частях. – 2015. – С. 119-122.
- Иванов В.К. Теория линейных некорректных задач и ее приложения / В. К. Иванов, В. В. Васин, В.П. Танана. – М.: Наука, 1978. – 200 с.
Список литературы на английском языке / References in English
- Modorskij V.Ja. Gazoprovod modeling of oscillatory processes in rocket engines solid fuel [Diagnosis of the stiffness characteristics of the rocket engine solid fuel] / V.Ja. Modorskij, A.V. Kozlova // Vestnik Samarskogo gosudarstvennogo tehnicheskogo universiteta. Serija: Fiziko-matematicheskie nauki. [Vestnik of Samara state technical University. Series: physics and mathematics.]. – 2006. №43. P. 163-167. [in Russian]
- Safina G.F. Modelirovanie v diagnostirovanii massovyh harakteristik raketnogo dvigatelja [Modeling in diagnosing the mass of the rocket engine] / G.F. Safina // Aktual'nye voprosy v nauchnoj rabote i obrazovatel'noj dejatel'nosti: sbornik nauchnyh trudov po materialam Mezhdunarodnoj nauchno-prakticheskoj konferencii: v 11 chastjah. [Current issues in research and educational activity: collection of scientific works on materials of the International scientific-practical conference: in 11 parts.]. – 2014. – P. 86–88. [in Russian]
- Safina G.F. Diagnostirovanie zhestkostnyh harakteristik raketnogo dvigatelja tverdogo topliva [Diagnosis of the stiffness characteristics of the rocket engine solid fuel] / G.F. Safina // Teoreticheskie i prikladnye voprosy nauki i obrazovanija: sbornik nauchnyh trudov po materialam Mezhdunarodnoj nauchno-prakticheskoj konferencii: v 16 chastjah. [Theoretical and applied problems of science and education: collection of scientific works on materials of the International scientific-practical conference: in 16 parts.]. – 2015. P. 119-122. [in Russian]
- Ivanov V.K. Teorija linejnyh nekorrektnyh zadach i ee prilozhenija [The theory of linear incorrect problems and its applications] / V. K. Ivanov, V. V. Vasin, V.P. Tanana. – M.: Nauka, 1978. – 200 p. [in Russian]
