ИМИТАЦИОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РЕГИСТРАЦИИ И КОНТРОЛЯ ВЫСОКОДИНАМИЧНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ПАКЕТА LAB VIEW

Жамбаловой С.Ц.

ORCID: 0000-0003-2599-2643, Аспирант кафедры, Санкт-Петербургский Горный университет

ИМИТАЦИОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РЕГИСТРАЦИИ И КОНТРОЛЯ ВЫСОКОДИНАМИЧНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ПАКЕТА LAB VIEW

Аннотация

Данная статья посвящена проблемам измерения и контроля высокодинамичных процессов и способы решения данной проблемы. Предложен алгоритм построения новой градуировочной характеристики, которая наиболее полно будет отражать поведение высокодинамичного процесса, что в свою очередь позволит повысить точность информационно-измерительной системы. Разработана модель информационно-измерительной системы для измерения и контроля высокодинамичных процессов, построенная в среде графического программирования Lab View.

Ключевые слова: имитационная математическая модель, высокодинамичные процессы, повышение точности.

Zhambalova S.Ts.

ORCID: 0000-0003-2599-2643, Postgraduate student, Saint-Petersburg Mining University

IMITATIONAL MATHEMATICAL MODEL OF REGISTRATION AND CONTROL OF HIGHLY DYNAMIC  PROCESSES WITH LAB VIEW SOFTWARE

 Abstract

The paper is devoted to the problems of measure and control of highly dynamic processes and how to solve the problem. The author proposes the algorithm for construction of a new calibration curve, it most fully reflects the behavior of a highly dynamic process, which in turn improves the accuracy of the information-measuring system. The model of the information-measuring system for measure and control of high-dynamic processes, developed in the graphical programming software Lab View is developed as well.

Keywords: imitational mathematical model, highly dynamic processes, increasing accuracy.

В промышленности, в технике, в природе всегда присутствуют случайные стохастические высокодинамичные процессы. Процессы, имеющие случайный характер распространения во временной плоскости и сложно предсказать их изменения в следующий момент времени, называются высокодинамичными процессами. К примеру, процесс перекачки, либо транспортировки нефти можно отнести к высокодинамичным процессам, рассматривая информационно-измерительную систему для определения свободного газа в нефти, т.к. содержание свободного газа при измерении, имеет случайный характер. Особенности высокодинамичных процессов вызывают трудности в реализации численных моделей. Это связано, прежде всего, с требованием проведения вычислительных процедур в реальном масштабе времени. При регистрации процесса, средства измерения фиксируют измеряемую величину не непрерывно, а лишь через определенный интервал времени, что увеличивает погрешность измерительной системы. Предел допускаемой относительной погрешности измерений массы нетто добываемой нефти - 0,4%, учитывая, что средняя годовая норма нефти нетто, для одной скважины около 9000 тонн, то данная погрешность составляет 36 тонн, что соответствует приблизительной годовой норме одного из участков объекта добычи.

При изучении и моделировании измерения и контроля высокодинамичных процессов необходимо решить три основные проблемы. Во первых, автоматическое управление технологическими процессами и оперативное эргодическое управление возможно на основе наиболее полной информации как о параметрах процесса, так и при наличии высокочувствительных, быстродействующих измерительных средств, способных обменять энергию на информацию.

Вторая проблема – это сохранить сигнал, полученный при измерении физических параметров и обрабатываемый во вторичных приборах. Поскольку для стохастических процессов трудно измерить и представить этот сигнал в нужной форме (Добротность и средства  - сочетает погрешность  с быстродействием t и мощностью измерения P). Сочетание энергопотребления, быстродействия и точности, как правило не удовлетворяют реальной динамике процесса.

Для описания различных высокодинамичных процессов применяют математическое моделирование, его рассматривают как инструмент для изучения исследуемых процессов, которые сопровождают работу системы, путем их замены на процессы более удобные для исследования, заменяемые процессы сохраняют основные требуемые свойства оригинала в зависимости от поставленной задачи. [1]

Для отображения высокодинамичных процессов так же можно использовать простейшие модели, такие как: пуассоновский поток, отрицательно-биномиальный поток, поток Бернулли. Сигнал потока исследуемой плотности жидкости представляет собой белый шум, имеющий пуассоновское распределение автокорреляционную функцию в виде дельта функции. При протекании газожидкостной смеси пуассоновский белый шум модулируется коррелированным случайным процессом изменения плотности, возникающим за счет флуктуаций содержания газа в потоке.

Стационарные процессы с ограниченным спектром частот в виде периодических случайных реализаций могут быть представлены случайными колебаниями по Райсу, данная модель более универсальна. Фактически модель Райса описывает временную периодическую реализацию с периодом Т посредством гармонического ряда Фурье со случайными амплитудами и фазами составляющих гармоник (см. Рис.1). Важной является заключенная в самой модели фундаментальная связь между числом гармоник и интервалом периодичности Т. [1]

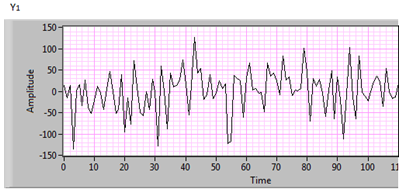
Рис. 1 - Пример реализации высокодинамичного процесса в среде LabView

И третье – для измерительных систем присущи мультипликативные и аддитивные погрешности, которые периодически нужно компенсировать. В работе принят для этой цели метод скользящего окна:

где

амплитуда функции f(x) автоматически измеряется бортовым компьютером, который также корректирует градуировочную характеристику и средства по методике. Автоматическая коррекция градуировочной характеристики осуществляется по двум точкам: ноль и чувствительность. Дискретизация по времени Δt для измерений и для момента корректирования подбирается экспериментально.

Алгоритм построения градуировочной характеристики измерительных приборов для измерения и контроля высокодинамичных процессов (см. рис.2) состоит из следующих этапов: сбор измерительной информации, ввод данных, выбор шага дискретизации, построение градуировочной характеристики, автоматическая коррекция градуировочной характеристики, вывод данных.

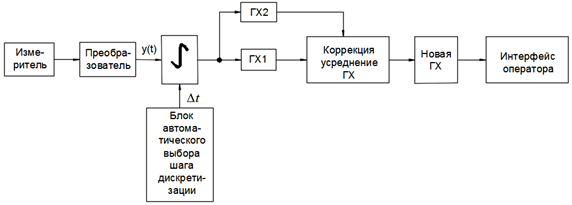
Рис.2 - Структурная схема метода повышения точности

Для повышения точности измерений, предлагается автоматическая коррекция градуировочной характеристики. Данные с исследуемого объекта через измеритель и преобразователь поступают на блок с градуировочной таблицей, в соответствии с которой формируется градуировочная характеристика 1 (ГХ). Параллельно строится ГХ2 по методу наименьших квадратов (МНК). Затем происходит автоматическая корректировка ГХ (см. Рис3). Градуировочная характеристика описывается линейной зависимостью по формуле 1. [2,3]

   (1)

где градуировочная характеристика описывается зависимостью Х, а₀, а₁ – коэффициенты описывающие прямую, Q- аргумент.

Критерий наименьших квадратов, согласно формуле 2:

  (2)

Результат уточняется путем усреднения и занесение в память устройства как новая уточненная градуировочная характеристика. Описанная процедура повторяется непрерывно в течение всего периода работы устройства – новая характеристика усредняется с предварительно многократно усредненной (и теперь уже являющейся базовой) градуировочной характеристикой.

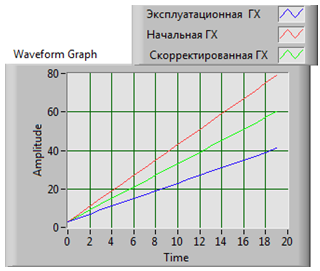
Рис.3 - Построение ГХ в среде Лаб Вью

Зависимость синего цвета – это зависимость, характеризующая значения, снятые с датчиков ГХ1; зависимость синего цвета – вычисленное множество, которое характеризует измеряемую физическую величину (ГХ2 рассчитанная по МНК); зависимость зеленого цвета - базовая градуировочная характеристика

На блок корректировки ГХ подается сигнал с интегратора, который несет информацию о шаге дискретизации. Интервал между отсчетами выбирается автоматически в зависимости от характера поведения высокодинамичного процесса. Можно выделить две основные группы методов: равномерную и неравномерную дискретизацию. При равномерной дискретизации функции x(t) на всем рассматриваемом диапазоне D_t изменения аргумента интервал между отсчетами неизменен (Δ_T=const). Величина этого интервала (шаг равномерной дискретизации) Δ_T выбирается на основе априорных сведений и характеристиках сигнала, экспериментальным путем, в соответствии с характером поведения исследуемого процесса, при неравномерной дискретизации интервал между отсчетами изменяется по случайному закону или с учетом изменения характеристик сообщения (адаптивная дискретизация).

Итак, подводя итоги, можно констатировать следующее:

1) предложена методика автоматической корректировки градуировочных характеристик, которая позволит уменьшить статистические погрешности до минимальных значений.

2) разработана имитационная модель на основе вышеописанной методике. Моделирование проводилось на базе имитационной модели виртуального прибора собранного с помощью пакета Lab View.

Список литературы / References

1. Жамбалова С.Ц. Проблемы измерения высокодинамичных процессов в электромеханических системах / С.Ц. Жамбалова, В.А. Шпенст//. Современная наука: актуальные проблемы теории и практики. Серия «Естественные и Технические науки». – 2016. - № 1 – С.18-22
2. Садовский Г.А. Теоретические основы информационно-измерительной техники / Г.А Садовский. - М., 2008 – 478 с.
3. Шишкин И.Ф. Теоретическая метрология, Часть 1 / И.Ф Шишкин. – Санкт-Петербург: Питер, 2010 – 192с.

Список литературы на английском языке / References in English

1. Zhambalova S.C. Problemy izmerenija vysokodinamichnyh processov v jelektromehanicheskih sistemah [Problems of measuring high-dynamic processes in electromechanical systems] / S.C. Zhambalova, V.A. Shpenst//. Sovremennaja nauka: aktual'nye problemy teorii i praktiki. Serija «Estestvennye i Tehnicheskie nauki» [Modern science: actual problems of theory and practice. Series "Natural and Engineering Sciences"]. – 2016. - № 1 – P.18-22 [in Russian]
2. Sadovskij G.A. Teoreticheskie osnovy informacionno-izmeritel'noj tehniki [Theoretical basis of information and measuring technology] / G.A Sadovskij. - M., 2008 – 478 p. [in Russian]
3. Shishkin I.F. Teoreticheskaja metrologija, Chast' 1 [Theoretical metrology, Part 1 / I.F Shishkin. – Sankt-Peterburg: Piter, 2010 – 192p [in Russian].