ЧАСТОТНАЯ ЗАВИСИМОСТЬ ЛОКАЛИЗАЦИИ ИНДУКЦИОННЫХ ТОКОВ
Черных А.Г.
ORCID: 0000-0003-4857-9560, Кандидат физико-математических наук, Красноярский государственный педагогический университет им. В.П. Астафьева
ЧАСТОТНАЯ ЗАВИСИМОСТЬ ЛОКАЛИЗАЦИИ ИНДУКЦИОННЫХ ТОКОВ
Аннотация
Рассмотрена динамика изменения структуры индукционных токов с ростом частоты внешнего квазистационарного магнитного поля. Проведено численное решение системы уравнений Максвелла, описывающих физику задачи. Индукционные токи определяются амплитудой и фазовым сдвигом относительно внешнего поля. Из-за обратных связей, обусловленных уравнениями Максвелла индукционные токи имеют сложную структуру, особенностью которой является наличие радиальных координат и частот, при которых токи в скин-слое движутся в противофазе.
Ключевые слова: уравнения Максвелла, цилиндрический проводник, индукционные токи, квазистационарное магнитное поле, фазовый сдвиг.
Chernykh A.G.
ORCID: 0000-0003-4857-9560, PhD in Physics and Mathematics, Krasnoyarsk State Pedagogical University named after V.P. Astafiev
FREQUENCY DEPENDENCE OF INDUCTION CURRENTS LOCALIZATION
Abstract
The dynamics of changes in the structure of induction currents with increasing frequency of the external quasistationary magnetic field is considered in the paper. A numerical solution of the system of Maxwell’s equations describing the physics of the problem is carried out. The induction currents are determined by the amplitude and the phase shift relative to the external field. Because of the feedbacks caused by Maxwell's equations, induction current have a complex structure, and its distinctive feature is the presence of radial coordinates and frequencies at which the currents in the skin layer move in reverse phase.
Keywords: Maxwell's equations, cylindrical conductor, induction currents, quasistationary magnetic field, phase shift.
Задача описания взаимодействия цилиндрического проводника с квазистационарным магнитным полем, параллельным оси проводника, рассмотрена в работах [1], [2, С. 310]. Показано, что индукционные токи определяются функциями Бесселя. Аргументом этих функций является величина ![]() где
где ![]() , r – радиальная координата
, r – радиальная координата ![]() , δ – толщина скин-слоя. Функции Бесселя неудобны для анализа полученных закономерностей, поэтому вычислены только две асимптотики:
, δ – толщина скин-слоя. Функции Бесселя неудобны для анализа полученных закономерностей, поэтому вычислены только две асимптотики: ![]() и
и ![]() . Первая асимптотика – предельно низкие частоты ω внешнего поля – приводит к очевидному результату: плотность тока пропорциональна rω, индукционный ток сдвинут по фазе относительно внешнего поля на величину π/2. Вторая асимптотика – предельно большие ω – показывает, что индукционный ток локализован в тонком поверхностном слое толщиной δ. Фазовый сдвиг индукционных токов эта асимптотика не определяет. Цель данной работы – изучение динамики изменения параметров индукционных токов с ростом частоты внешнего поля.
. Первая асимптотика – предельно низкие частоты ω внешнего поля – приводит к очевидному результату: плотность тока пропорциональна rω, индукционный ток сдвинут по фазе относительно внешнего поля на величину π/2. Вторая асимптотика – предельно большие ω – показывает, что индукционный ток локализован в тонком поверхностном слое толщиной δ. Фазовый сдвиг индукционных токов эта асимптотика не определяет. Цель данной работы – изучение динамики изменения параметров индукционных токов с ростом частоты внешнего поля.
Фазовый сдвиг индукционных токов эта асимптотика не определяет. Цель данной работы – изучение динамики изменения параметров индукционных токов с ростом частоты внешнего поля.
Рассмотрим ситуацию: проводник в форме сплошного длинного цилиндра, радиус которого a, проводимость σ, помещен в однородное переменное магнитное поле ![]() , параллельное оси цилиндра. Геометрия задачи симметрична относительно оси цилиндра, поэтому вихревые токи будут течь по окружностям в плоскостях, перпендикулярных его оси. Это означает, что параметры тока зависят от радиальной координаты r и ω. При гармонической зависимости внешнего магнитного поля от времени, напряженность поля удобно представить в комплексном виде:
, параллельное оси цилиндра. Геометрия задачи симметрична относительно оси цилиндра, поэтому вихревые токи будут течь по окружностям в плоскостях, перпендикулярных его оси. Это означает, что параметры тока зависят от радиальной координаты r и ω. При гармонической зависимости внешнего магнитного поля от времени, напряженность поля удобно представить в комплексном виде:
![]()
Магнитное поле внутри проводящего цилиндра определяется уравнениями Максвелла в квазистационарном приближении [1], [2]. Зависимость магнитного поля от t и r имеет вид
![]()
Толщина скин-слоя определяется формулой ![]() В (1) входят функции Бесселя нулевого порядка [3, С. 112]:
В (1) входят функции Бесселя нулевого порядка [3, С. 112]:


Соотношения (2–4) определяют точное решение уравнений Максвелла в квазистационарном приближении. Выражение (3) приведем к виду, удобному для применения методов вычислительной математики. Рассмотрим ![]() – ряд, являющийся знаменателем в формуле (3). В (2) учтем, что
– ряд, являющийся знаменателем в формуле (3). В (2) учтем, что ![]() и
и ![]() .
.
Введем безразмерную переменную
![]()
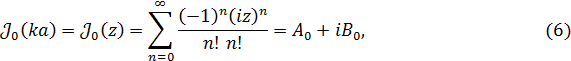
Ряды (7) и (8) знакопеременные, поэтому их можно численно суммировать с заданной точностью.
Проведем аналогичные преобразования выражения ![]() , стоящего в числителе (3). Используя соотношение (4), получим
, стоящего в числителе (3). Используя соотношение (4), получим
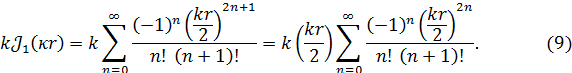
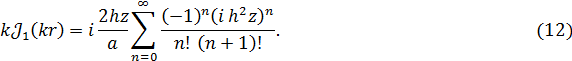 Это позволяет записать формулу для плотности вихревых токов
Это позволяет записать формулу для плотности вихревых токов 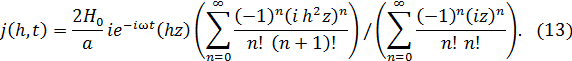 Представим сумму, стоящую в числителе (13) в виде комплексной величины
Представим сумму, стоящую в числителе (13) в виде комплексной величины
 где
где
Используя выделенные действительные и мнимые части рядов, выражение (13) запишем в виде
![]()
Действительная часть выражения (17) описывает плотность вихревых токов от относительного радиуса и времени. Можно показать, что

где
![]()
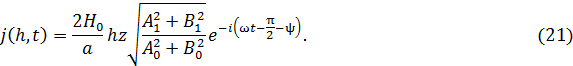 Действительная часть (21) имеет вид
Действительная часть (21) имеет вид
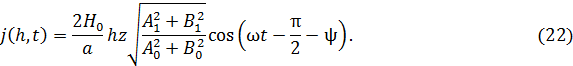 Безразмерное соотношение
Безразмерное соотношение

с точностью до постоянного множителя ![]() определяет амплитуду плотности вихревых токов. Величина
определяет амплитуду плотности вихревых токов. Величина
![]()
определяет фазовый сдвиг плотности токов относительно внешнего поля.
Проведенное преобразование рядов, определяющих амплитуду плотности индукционного тока и фазовый сдвиг тока относительно внешнего поля, показало, что характеристики вихревого тока определяются безразмерными величинами z и h. Анализ зависимости амплитуды плотности индукционных токов и фазового сдвига тока относительно внешнего поля проведем на основе численно построенных графиков. Аргументом этих функций является величина z, пропорциональная чистоте внешнего поля. Графики строятся при значении h, равных 0,25; 0,75; 0,95. Программа численного построения графиков опубликована в [5]. На рис. 1 показаны графики зависимости ![]() и
и ![]() при
при ![]() . Из графика видно: индукционный ток отличен от нуля при
. Из графика видно: индукционный ток отличен от нуля при ![]() . Плотность тока с ростом z сначала быстро растет, затем более медленно спадает до нуля. В интервале z, где ток отличен от нуля, есть два значения z, при которых фазовый сдвиг меняется от нуля до π. Это означает, что в окрестности этих z ток меняет направление движения на противоположное, - с ростом z структура токов сильно меняется.
. Плотность тока с ростом z сначала быстро растет, затем более медленно спадает до нуля. В интервале z, где ток отличен от нуля, есть два значения z, при которых фазовый сдвиг меняется от нуля до π. Это означает, что в окрестности этих z ток меняет направление движения на противоположное, - с ростом z структура токов сильно меняется.
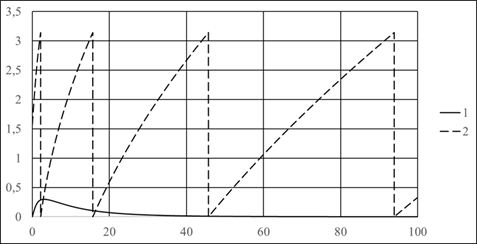
Рис. 1 – Зависимость безразмерной амплитуды плотности индукционного тока и разности фаз между током и внешним магнитным полем от z , при ![]() : 1 – амплитуда плотности тока; 2 – разность фаз
: 1 – амплитуда плотности тока; 2 – разность фаз
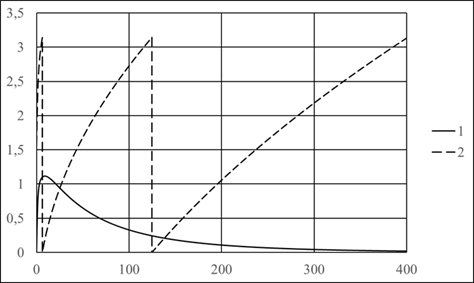
Рис. 2 – Зависимость безразмерной амплитуды плотности индукционного тока и разности фаз между током и внешним магнитным полем от z , при ![]() : 1 – амплитуда плотности тока; 2 – разность фаз
: 1 – амплитуда плотности тока; 2 – разность фаз
Графики на рис. 2 качественно повторяют графики на рис. 1. На рис. 3 показаны графики зависимости ![]() и
и ![]() при
при ![]() .
.
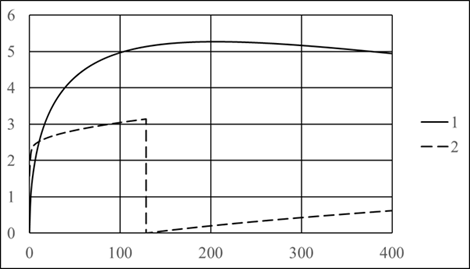
Рис. 3 – Зависимость безразмерной амплитуды плотности индукционного тока и разности фаз между током и внешним магнитным полем от z, при ![]() : 1 – амплитуда плотности тока; 2 – разность фаз
: 1 – амплитуда плотности тока; 2 – разность фаз
Из графиков на рис. 3 видно, что при ![]() амплитуда индукционных токов максимальна при
амплитуда индукционных токов максимальна при ![]() . С ростом z амплитуда медленно убывает: токи концентрируются ближе к поверхности цилиндра. Скачок фазы при
. С ростом z амплитуда медленно убывает: токи концентрируются ближе к поверхности цилиндра. Скачок фазы при ![]() означает, что ток в окрестности
означает, что ток в окрестности ![]() с ростом z меняет направление на противоположное.
с ростом z меняет направление на противоположное.
Список литературы / References
- Ландау Л. Д. Теоретическая физика: учеб. пособие. В 10 т. Т. 8. Электродинамика сплошных сред / Л. Д. Ландау, Л. П. Питаевский, Е. М. Лифшиц; под ред. Л. П. Питаевского. 4-е изд., стер. – М.: Физматлит, 2003. – 652 с.
- Батыгин В. В. Сборник задач по электродинамике: учеб. пособие / В. В. Батыгин, И. Н. Топтыгин; под ред. М. М. Бредова. 3-е изд., испр. – Ижевск; М.: НИЦ «Регулярная и хаотическая динамика», 2002. – 640 с.
- Никифоров А. Ф., Уваров В.Б. Специальные функции математической физики / под ред. А. А. Самарского. – М.: Наука, 1978. – 320 с.
- Черных А. Г. Бесконтактное измерение электросопротивления проводников в переменном магнитном поле. Ч. 2 / А.Г. Черных // Физическое образование в вузах. – 2013. Т. 19. – № 3. – С. 138–150.
- Черных А.Г. Расчет процесса самоорганизации вихревых индукционных токов в массивном проводнике цилиндрической формы при изменении частоты внешнего квазистационарного магнитного поля: свидетельство о гос. регистрации программы для ЭВМ № 2017611384 Рос. Федерация / А.Г. Черных; заявл. 29.09.2016; опубл. 02.02.2017. Бюл. № 2.
Список литературы на английском языке / References in English
- Landau L. D. Teoreticheskaja fizika: ucheb. posobie. V 10 t. T. 8. Jelektrodinamika sploshnyh sred [Electrodynamics of Continuous Media, Second Edition: V. 8. Course of Theoretical Physics, 2nd ed.] / L. D. Landau, L. P. Pitaevskii, E. M. Lifshitz. – Published by USA.: Butterworth-Heinemann, 1984.
- Batygin V. V. Sbornik zadach po jelektrodinamike: ucheb. posobie [Problems in Electrodynamics] / V. V. Batygin, I. N. Toptygin. – London: Academic Press, 1978.
- Nikiforov A. F., Uvarov V. B. Specialnye funkcii matematicheskoj fizik [Special functions of mathematical physics] / pod red. A. Samarskogo [Ed. А. А. Samarsky]. – M.: Nauka, 1978. – 320 pp. [In Russian]
- Chernykh A. G. Beskontaktnoe izmerenie ehlektrosoprotivleniya provodnikov v peremennom magnitnom pole. Ch 2 [Contactless measurement of electrical resistance in alternating magnetic field. Part 2] / A. G. Chernykh // Fizicheskoe Obrazovanie v VUZah [Physics in Higher Education]. – 2013 T. 19. –№ 3. – P. 138–150. [In Russian]
- Chernykh A. G. Raschet processa samoorganizacii vihrevyh indukcionnyh tokov v massivnom provodnike cilindricheskoj formy pri izmenenii chastity vneshnego kvazistacionarnogo magnitnogo polya svidetelstvo o gos. registracii programmy dlya EhVM 2017611384 Ros. Federaciya [Calculation of the process of self organization of vortex induction currents in a massive conductor of cylindrical shape with a change in the frequency of an external quasistationary magnetic field: Registration of the computer program № 2017611384 Ros. Federation] / A. G. Chernykh; zayavl. 09.29.2016; publ. 02.02.2017. bul. № 2. [In Russian]
