ВЛИЯНИЕ МНОГОЛУЧЕВОГО РАСПРОСТРАНЕНИЯ РАДИОВОЛН В ГОРОДСКИХ УСЛОВИЯХ НА ЭНЕРГЕТИЧЕСКУЮ ДОСТУПНОСТЬ РАДИОСРЕДСТВ УКВ ДИАПАЗОНА
ВЛИЯНИЕ МНОГОЛУЧЕВОГО РАСПРОСТРАНЕНИЯ РАДИОВОЛН В ГОРОДСКИХ УСЛОВИЯХ НА ЭНЕРГЕТИЧЕСКУЮ ДОСТУПНОСТЬ РАДИОСРЕДСТВ УКВ ДИАПАЗОНА
Научная статья
Тамилин В.Л.¹, Панычев С.Н.²
¹Воронежский институт МВД России, Воронеж, Россия
²Воронежский государственный технический университет, Воронеж, Россия
Aннотация
В статье рассматривается один из видов энергетической доступности при разнесенном оптимальном посимвольном приеме, который способен полностью устранить потери энергетики радиолиний, вызванные медленными замираниями. Проведен анализ схем повышения помехоустойчивости при разнесенном оптимальном посимвольном приеме и разнесенном оптимальном с квадратичным сложением приеме.
Ключевые слова: помехоустойчивость, модуляция, мендленные замирания, многолучевое распространение.
Keywords: noise stability, modulation, mendlenny dying down, multibeam distribution.
Введение
Одним из наиболее распространенных эффектов распространения сигналов в городских условиях является возникновение многолучевого распространения сигнала между передатчиком и приемником.
Распространение радиосигнала в городских условиях кардинально отличается от условий распространения прямой видимости. Помимо всех помех и шумов, появляется множество дополнительных, нежелательных эффектов. Наличие большого количества застроек, высотных зданий, труб, структура улиц, возможные перепады уровня земной поверхности и т. п. приводят к многократному отражению сигнала. Даже если приемное устройство находится в стационарном состоянии, уровень принимаемого сигнала может меняться за счет отражений от движущихся транспортных средств[1-4]. В результате на приемную антенну практически всегда приходит множество копий сигнала с разными уровнями и разными задержками по времени.
В связи с этим задача совершенствования методов оптимального разнесенного приема радиолиний, вызванных медленными замираниями является актуальной.
Целью статьи является обоснование и упрощение оптимального алгоритма совместной обработки, именуемого когерентным сложением с весами.
Метод с разнесением по пространству приемных антенн с текущим отношением сигнал/шум
В этом варианте передача сообщения соответствует случаю канала без замираний. Для приема используется несколько приемных антенн, расположенных на расстояниях, превосходящих интервал корреляции канала по пространству. Замирания сигналов на выходах этих антенн должны оказаться взаимно независимыми.
Сигналы с выходов всех приемных антенн (со всех ветвей разнесения) поступают на общее устройство их совместной обработки, которое и формирует демодулированное сообщение [2,3]. Возможны различные алгоритмы совместной обработки, причем их выбор существенно влияет на эффективность борьбы с замираниями. Эта эффективность зависит, в частности, от объема сведений о сигнале каждой ветви, которые используются при обработке. К таким сведениям относятся: текущее отношение сигнал/шум ветви h, (j = 1, 2,...,n), спектральная плотность N0, шумов в ней, взаимный сдвиг фаз между полезными сигналами отдельных ветвей и др. Все эти параметры не бывают известны заранее и должны определяться в реальном времени, для чего в устройства совместной обработки включают соответствующие анализаторы. Очевидно, что определение указанных параметров в реальных каналах связи представляет собой достаточно сложную задачу, сопряженную с необходимостью реализации весьма сложных устройств. Это и объясняет стремление к упрощению алгоритмов совместной обработки, чем и определяется рассмотрение в нижеследующем материале нескольких таких алгоритмов.
Начнем с анализа оптимального алгоритма совместной обработки, именуемого когерентным сложением с весами. Речь идет о том, что в устройстве совместной обработки напряжения ветвей Zj(t) когерентно (по полезному сигналу) суммируются, причем каждому напряжению приписывается определенный вес 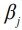 , так что суммарный сигнал
, так что суммарный сигнал

Суммарное напряжение подается на обычный демодулятор для выделения сообщения. Поясним смысл введения весов (суммарное напряжение подается на обычный демодулятор для выделения сообщения). В (1) веса обозначены 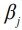 . Напряжения ветвей содержат как полезный сигнал xt(t), так и шумы
. Напряжения ветвей содержат как полезный сигнал xt(t), так и шумы 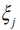 ; то же относится и к суммарному напряжению Z(t). В каждой ветви в каждый данный момент времени имеет место свой, отображающий замирания, коэффициент передачи канала
; то же относится и к суммарному напряжению Z(t). В каждой ветви в каждый данный момент времени имеет место свой, отображающий замирания, коэффициент передачи канала 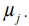
В тех каналах, где в данный момент коэффициент передачи оказывается много меньше единицы, напряжение ветви содержит почти исключительно шум, так что добавление этого напряжения к (1) лишь снизило бы отношение сигнал/шум в суммарном напряжении. Рассмотрим вопрос об оптимальном выборе весовых коэффициентов 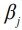 . Обозначим текущее значение отношений сигнал/шум по мощности в ветвях через параметр
. Обозначим текущее значение отношений сигнал/шум по мощности в ветвях через параметр

где 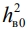 - среднее значение отношения мощностей сигнала и шума в ветви при
- среднее значение отношения мощностей сигнала и шума в ветви при 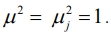 Поскольку ветви предполагаются подобными, принимается, что для всех них значение
Поскольку ветви предполагаются подобными, принимается, что для всех них значение 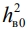 одинаково. Для определения суммарной амплитуды Z(t) обозначим, отношение сигнал/шум по мощности через h2.
одинаково. Для определения суммарной амплитуды Z(t) обозначим, отношение сигнал/шум по мощности через h2.
Задача выбора весов 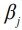 заключается в нахождении таких их значений, при которых h2 оказывается максимальным. Один из весов можно выбрать произвольно, вычисляя остальные относительно него. Такой выбор не повлияет на достижимое значение h2, а определит лишь результирующий уровень суммарного напряжения. Выберем
заключается в нахождении таких их значений, при которых h2 оказывается максимальным. Один из весов можно выбрать произвольно, вычисляя остальные относительно него. Такой выбор не повлияет на достижимое значение h2, а определит лишь результирующий уровень суммарного напряжения. Выберем 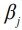 = 1.
= 1.
Примем мощности шумов во всех каналах одинаковыми и равными Pш, тогда мощность полезного сигнала в напряжении j-й ветви , 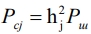 , а
, а
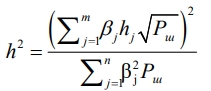
При записи соотношения (2) учтено, что при когерентном сложении суммируются амплитуды полезных сигналов ветвей [4]. Что же касается шумов, то в отдельных ветвях они считаются независимыми, так что суммируются их мощности (дисперсии).
Учтем теперь, что выбрано 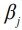 = 1 и рассмотрим пару ветвей — первую и некоторую под номером m. Если выбрать
= 1 и рассмотрим пару ветвей — первую и некоторую под номером m. Если выбрать 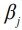 так, чтобы обеспечить максимум отношения сигнал/шум в напряжении, полученном от суммирования только данной пары ветвей, то можно утверждать, что это же значение
так, чтобы обеспечить максимум отношения сигнал/шум в напряжении, полученном от суммирования только данной пары ветвей, то можно утверждать, что это же значение 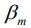 будет наилучшим и с точки зрения максимизации всей суммы (2). Действительно, любое другое значение
будет наилучшим и с точки зрения максимизации всей суммы (2). Действительно, любое другое значение 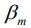 ухудшило бы результат суммирования напряжений первой и m-й ветвей, а, следовательно, и результат общего суммирования.
ухудшило бы результат суммирования напряжений первой и m-й ветвей, а, следовательно, и результат общего суммирования.
Итак, пусть в (2) n = 2. Взяв производную от этого соотношения по  и приравнивая ее к нулю, находим, что оптимальное значение веса
и приравнивая ее к нулю, находим, что оптимальное значение веса 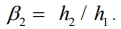
В соответствии с изложенным это означает, что для оптимальных значений всех весов имеют место соотношения

Подставляя найденные оптимальные значения весов в (2), найдем максимально возможное значение h:

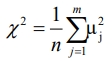 - случайная величина, характеризующая результирующие замирания, и
- случайная величина, характеризующая результирующие замирания, и 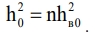 Случайная величина x2 представляет собой сумму квадратов независимых нормальных случайных величин, содержащую 2n членов.
Случайная величина x2 представляет собой сумму квадратов независимых нормальных случайных величин, содержащую 2n членов.
Рассмотрим лишь частный случай, когда суммируемые нормальные случайные величины центрированы и имеют одинаковые дисперсии [5]. В интересующем нас приложении это означает, что распределение величины x2 удается записать аналитически только для случая релеевских распределений коэффициентов передачи ветвей. В этом случае плотность распределения вероятностей для принимает x2 вид при

С помощью (5) можно вычислить среднюю вероятность ошибки на бит транслируемой последовательности в релеевском канале с медленными дружными замираниями при использовании n ветвей разнесения и когерентном сложении напряжений ветвей с оптимальными весами. Пусть, например, используется ОФМ с некогерентной демодуляцией, тогда получим:

Усредняя это выражение по распределению (5), окончательно получим, используя табулированные интегралы,

Отметим, что величина 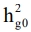 учитывает здесь среднее значение мощности суммарного сигнала, поступившего по всем ветвям разнесения. Поэтому данную величину следует считать неизменной при сопоставлении вариантов с разным числом ветвей, ибо это будет соответствовать постоянным энергетическим ресурсам, расходуемым на передачу канальной информации.
учитывает здесь среднее значение мощности суммарного сигнала, поступившего по всем ветвям разнесения. Поэтому данную величину следует считать неизменной при сопоставлении вариантов с разным числом ветвей, ибо это будет соответствовать постоянным энергетическим ресурсам, расходуемым на передачу канальной информации.
Результаты расчета по (7) представлены на рис. 2 для случаев использования двух, трех и четырех ветвей разнесения. Здесь показана для сопоставления и кривая, относящаяся к случаю отсутствия разнесения, повторяющая соответствующую зависимость на рис. 2. Отметим, что она полностью совпадает с зависимостью (6) для n = 1.
Рассмотрим как ведет себя вероятность ошибки при неограниченном возрастании числа ветвей разнесения, т.е. при 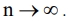 Переходя в (7) к соответствующему пределу и используя известное из математики определение числа e, согласно которому
Переходя в (7) к соответствующему пределу и используя известное из математики определение числа e, согласно которому  , получим
, получим

что полностью совпадает с помехоустойчивостью некогерентного приема ОФМ в канале без замираний. Таким образом, оптимальный разнесенный прием способен, в принципе, полностью устранить потери энергетики радиолиний, вызванные медленными замираниями.

Рис. 1. Помехоустойчивость при разнесенном оптимальном посимвольном приеме
Данные рис. 1. показывают, что уже при использовании двух ветвей разнесения при когерентном весовом сложении обеспечивается значительное снижение энергетических потерь, вызванных медленными дружными замираниями. Так, для вероятности ошибки эти потери снижаются с 19 до 8 дБ. Ситуация может быть улучшена за счет увеличения числа ветвей разнесения, однако выигрыш растет сравнительно медленно, а сложность оборудования значительно нарастает [6]. По этой причине число ветвей большее трех используется редко.
Как уже отмечалось выше, часто применяют упрощенные алгоритмы совместной обработки. Кратко остановимся на двух таких алгоритмах: квадратичного сложения и мажоритарном.
Алгоритмы квадратичного сложения и мажоритарный
Для пояснения идеи алгоритма квадратичного сложения используем структуру идеального некогерентного приемника.
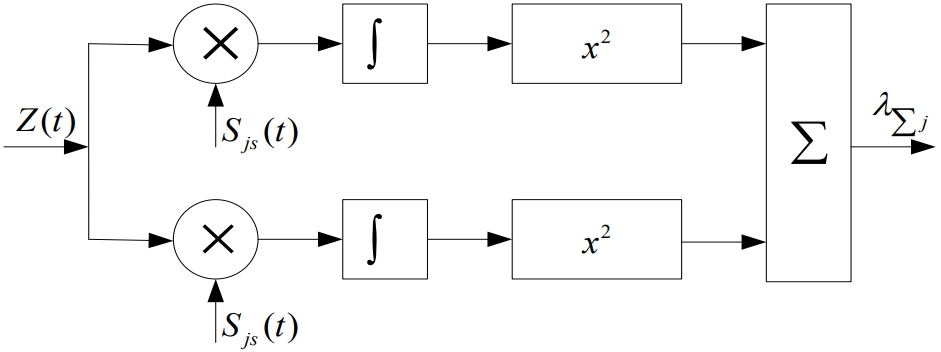
Рис. 2. Измеритель коэффициента правдоподобия для сигнала со случайной фазой
Решение относительно демодулированного символа в таком приемнике принимается на основе сравнения правдоподобия возможных элементарных сигналов  определяемых устройствами рис. 2. При разнесенном приеме с квадратичным сложением блоки таких измерителей коэффициентов правдоподобия используются в каждой ветви разнесения. В результате формируется (m×n) коэффициентов правдоподобия (m - число возможных значений транслируемых символа сообщения j=1,2,...m;). Обозначим коэффициенты правдоподобия через
определяемых устройствами рис. 2. При разнесенном приеме с квадратичным сложением блоки таких измерителей коэффициентов правдоподобия используются в каждой ветви разнесения. В результате формируется (m×n) коэффициентов правдоподобия (m - число возможных значений транслируемых символа сообщения j=1,2,...m;). Обозначим коэффициенты правдоподобия через 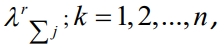 где k - номер ветви разнесения. При квадратичном сложении результирующие коэффициенты правдоподобия, формируются суммированием одноименных по нижнему индексу коэффициентов правдоподобия отдельных ветвей:
где k - номер ветви разнесения. При квадратичном сложении результирующие коэффициенты правдоподобия, формируются суммированием одноименных по нижнему индексу коэффициентов правдоподобия отдельных ветвей:

Таким образом, результирующие коэффициенты правдоподобия получаются суммированием по всем ветвям коэффициентов правдоподобия для каждого возможного символа сообщения.
Описанная процедура именуется квадратурным сложением, так как в соответствии с рис. 2 сами величины  получаются как суммы квадратов квадратурных компонент, а следовательно,
получаются как суммы квадратов квадратурных компонент, а следовательно,  - есть сумма таких квадратов, взятых с одноименных измерителей правдоподобия уже по всем ветвям разнесения.
- есть сумма таких квадратов, взятых с одноименных измерителей правдоподобия уже по всем ветвям разнесения.
После формирования результирующих коэффициентов правдоподобия, схема совместной обработки напряжений ветвей принимает решение о передававшемся символе сообщения по следующему естественному правилу: считается, что был передан тот символ, для которого  оказывается максимальным.
оказывается максимальным.
Квадратичное сложение существенно проще реализовать, чем оптимальное когерентное суммирование. Это следует уже из того, что оно использует гораздо меньше сведений о текущих параметрах напряжений в ветвях разнесения. Здесь не требуется знания отношений сигнал/шум и фаз сигналов ветвей. Относительно эффективности квадратичного суммирования ограничимся воспроизведением зависимостей, характеризующих его помехоустойчивость в каналах с дружными медленными релеевскими замираниями, взятыми из источника [6] (рис. 3).
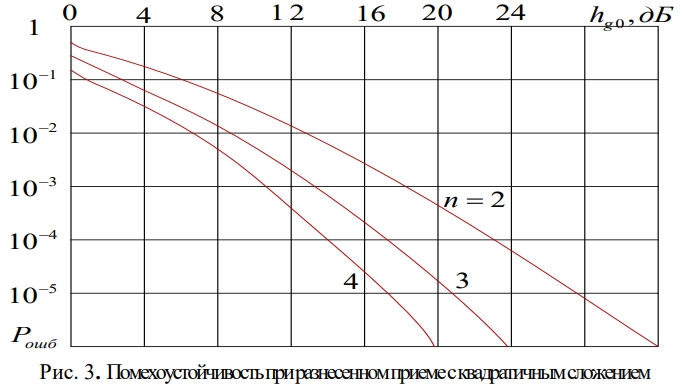
Сопоставляя данные рис. 1 и 3, убеждаемся, что хотя выигрыш от разнесения при оптимальном когерентном сложении больше, чем при квадратичном сложение, различие их не слишком велико (порядка 1-2 дБ).
Остановимся на мажоритарной совместной обработке. В этом варианте на каждом данном временном интервале используется сигнал только той ветви, которая по отношению сигнал/шум превосходит остальные. Если с течением времени указанное отношение в данной ветви перестает быть наибольшим, устройство совместной обработки переходит к приему сигналов другой ветви, вышедшей по этому показателю вперед. В соответствии с приведенным алгоритмом устройство мажоритарной обработки иногда именуют еще устройством автовыбора. Анализ, проведенный в ряде работ, показывает, что при такой обработке энергетический выигрыш от разнесения оказывается меньше, чем при квадратичном сложении на величину порядка 1 дБ.
Заключение
Таким образом, определение параметров сигналов в реальных каналах связи представляет собой достаточно сложную задачу, сопряженную с необходимостью реализации весьма сложных устройств. Это обстоятельство стимулирует поиск путей упрощения алгоритмов совместной обработки. Алгоритм, реализующий метод разнесенных приемных антенн при своей относительной простоте по эффективности приближается к традиционным алгоритмам (квадратурному и др.). Возможность упрощения технологии обработки сигналов при многолучевом распространении при этом достигается усложнением состава приемной установки. В целом предложенный методический подход позволяет существенно улучшить энергетическую доступность радиолиний.
Список литературы / References
- Уильямс Т. ЭМС для разработчиков продукции / Пер. с англ. под ред. B.C. Кармашева, JI.H. Кечиева. - М.: Издательский дом «Технологии», 2004.
- TR CISPR 16-3 (2003): Specification for radio disturbance and immunity measuring apparatus and methods - Part 3: CISPR technical reports. Технический Отчет 16-3 СИСПР, 2003, Технические отчеты СИСПР.
- GMR-1 GEO Mobile Radio-family-1ETSI TS101 376-5-5(2006) Part7 Radio interference physical layer specifications Sub-part7 Radio Transmission and Reception.
- Севостъянов С.В. Общая модель сложной антенно-фидерной системы для целей анализа внутриобъектовой электромагнитной совместимости // Вестник СОНИИР. - 2002. - № 2.
- Бузов А.Л. Оценка пространственно-энергетических характеристик вибраторных антенн на частотах, существенно отличающихся от рабочих // Антенны. - 2003. - № 9.
- Signal Processing for Mobile Communications handbook/ Edited by M Ibnkahla – NY CRC Press, 2004
- Burgueno A, Vilar E, Puigcerver M The land mobile satellite communication channel - Recording, statistics and channel model// IEEE trans Veh Tecnol 1991 vol 60 №5 P 343-392
