IMPROVING METHODS OF MODELING CANAL WAVES PROPAGATION PROCESS IN COAL SEAMS

IMPROVING METHODS OF MODELING CANAL WAVES PROPAGATION PROCESS IN COAL SEAMS

Research article

Кеnzhin B.М.¹, Smirnov Yu.M.²

^{1, 2} Каraganda State Technical University, Karaganda, Kazakhstan

Abstract

There has been analyzed the principal methods of modeling the process of canal waves propagation in coal seams when carrying out mining geophysical studies. There has been established that the wave guide moving into the surface of the elastic half-space doesn’t practically change the main properties of the interferential waves propagating in them. There has been recommended to use Fourier integral describing the single pulse spectrum for studying the registered seismograms. There have been formulated the main problems of improving physical processes modeling in coal seams when carrying out their geological studying

Ключевые слова: угольный пласт, геофизические исследования,  сейсмограмма, каналовая волна.

Key words: coal seams, geophysical studies, seismograms, canal wave.

In forecasting coal seam breaking by the methods of seismic X-raying and reflected waves there is analyzed the wave picture of Love and Relay interferential waves obtained on real seismograms. The visible record of interferential waves propagating in the unbroken coal seam (wave guide) is determined by physical-and-mechanical methods of studying enclosing rocks, coal seams, as well as the conditions of the experiment carrying out. In a broken coal seam, besides the factors mentioned the visible record of interferential waves is affected by the breaking character (coal seam thinning, tearing, folding, etc.). To determine the extent of the factors mentioned affect on the registered wave filed there is used the method of mathematical modeling. A great contribution to the developing of the theory of interferential waves was made by V.I. Keilis-Borok, L.M. Brekhovskikh, A.L. Levshin [1].  In [2] based on the analysis of the reflected and refracted surface waves main properties there has been developed the methodology of their separating on seismograms and methods of determining the reflecting and refracting borders.

The developing of new numerical methods of differential equation solution, elasticity theory there appeared new possibilities to study interferential waves fields in different medium. In these cases there is used the method of the continuum discretion, which permits, as compared to other methods, to consider the models of real mediums characterized by a complicated structure. Here to study Love surface waves in three-dimension structures there is used the finite elements method (FEM). With the help of the finite differences there is studied Love canal waves propagation in two-dimension models of coal seams with different types of breakings.

The most common theory of surface and canal waves based on the spectral theory of differential operators was developed in [2]. Here at the physical level of strictness there was solved the problem of surface and canal waves propagation in vertically heterogeneous media, whose parameters (speed and density) are arbitrary discrete-and-continuous functions of depth. Based on the solution obtained there were developed the methods of calculation and studied the main properties of these waves.

The problem posed is reduced to solving heterogeneous differential equations of the second order with preset homogeneous boundary conditions (Sturm-Liuville problem). This problem is solved by means of series expansion by the own functions of differential operators, and the obtained accurate formulae of shifting in Love and Relay waves are expressed through the own functions of the corresponding one-dimension boundary problems of Sturm-Liuville type.

Based on the theoretical apparatus obtained there was developed the methodology of mathematical modeling consisting of several stages. At each stage there are solved certain physical problems: dispersion calculation, polarization, absorption, amplitude spectrum dependence on the receiver depth and source, shifting spectra of separate harmonics, and at the last stage – calculating theoretical seismograms of Love and Relay interferential waves.

The main properties of surface and canal waves are studied based on the common theory of own functions and numerous calculations for some models of ideal elastic media. From the formulae obtained in [2] it follows that each seismogram of interferential ( surface and canal) wave of Love and Relay type can be considered as a superposition of the infinite number of harmonics (normal waves, overtones, modes) corresponding to the shifting component  g. Harmonic number К changes in the limits I<k<∞. The expression for shifting the g component of the  k harmonic has the form (χ):

where U_kg (w) has the meaning of shifting spectral density; g component,  k harmonic.

In its turn, spectral density U_kg(w) can be presented as a product:

Based on the results obtained in [2], it can be concluded that the wave guide moving from the surface of the elastic half-space (surface wave guide) inside (inner wave guide) doesn’t practically change the main properties of interferential waves (surface and canal) propagating in them. Both surface and canal waves of Love and Relay type present a superposition of the infinite number of harmonics (modes). Each their harmonic is characterized by its boundary (critical) frequency ωкр, phase dispersion V_kg'(ω) and group dispersion C_kg'(ω) of speed, shifting by the amplitude dependence both on frequency and the receiver depth and source and other properties.

The first theoretical study of canal waves dispersion based on the matrix method of Tompson-Haskell was carried out by T. Krey. These works became the base for the further studies in the field of coal mining seismic exploring.

At PNIUI (Moscow coal scientific research institute, Tula) there were developed and realized the programs of fast Fourier transform for calculating theoretical seismograms and their spectra for the model of low-speed layer bedding between two identical isotropic half-spaces.

At UkrNIMI of theUkrainebased on the theory of interferential waves developed by A.L. levshin and B.I. Keilis-Borok, as well as on the results of T. Krey’s works there were developed the programs for calculating dispersion and theoretical seismograms of canal waves of Love and Relay type for multi-layer media.

Let’s imagine a coal seam as a flat-parallel layer with parameters Н_у,  ρ_y, V_sy, V_py, where  Н  is thickness, ρ_y is density, V_sy and V_py are speeds of transverse and longitudinal waves in the coal. The half-space parameters are ρ_п,V_SпV_pп.  Let’s introduce an orthogonal coordinate system (X, Y, Z). The axe  is a horizontal vector source-receiver. The axe  is directed horizontally and the axe 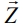 vertically. The coordinates beginning is located in the point which is equidistant to the coal seam boundaries. In this point let’s locate a pulse source of elastic vibrations with the spectrum S₀(f), whose action is directed on the axe .

At the distance  X = Z from the source the theoretical seismograms of interferential waves will have the form [2]:

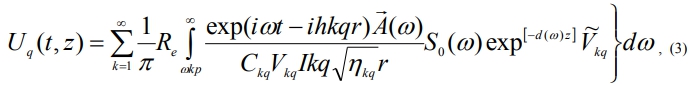
where q is a shifting component (Y – for Love waves, X and Z – for Relay waves); t is the time; Z is vertical coordinates; ω is an angular frequency; η_kqis  the wave number; k is the mode number;   С_kq is phase speed dispersion; V_kq is the function of amplitude shifts; А(ω) is the spectrum of the equipment; S_o(ω) is the spectrum of the source; V_kq is group speed dispersion.

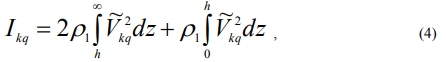
C_kq and V_kq are calculated by the formulae presented in work [1].

Thus, using the program of fast Fourier transform, we obtain theoretical seismograms and their amplitude spectra for different coefficients of absorption. Analyzing the data obtained after mathematical modeling, we can determine the band of frequencies in which there must be significant energy. Defines the presence of geological breaking. However, in spite of great possibilities of mathematical modeling, a lot of questions, such as establishing the breaking types, their affect on kinematical, dynamical and spectral characteristics of interferential waves are still uninvestigated.

Every oscillating process can be presented in two coordinate systems: amplitude-time and amplitude-frequency. In the first case oscillations have the form of oscillograms, seismograms, and in the second case we speak of the spectral structure of oscillations. Fourier transform connects the time and frequency fields of oscillations. Direct Fourier transform is of the form:

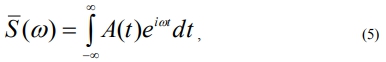
where  is a complex spectrum of the time function; ω is an angular frequency;  t is time.

Reverse Fourier transform is of the form:

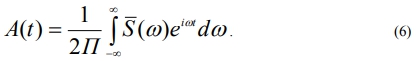
To study spectra of the registered seismograms it’s necessary to use Fourier integral (5), describing a single pulse spectrum.

To study the registered canal waves dispersion there is used the method of seismograms computer processing  described in [4].

On the two-dimension presentation of the wave processes there was developed СВАН program. To define the correctness of  these programs operation there is calculated canal waves theoretical seismograms dispersions, i.e. the process is modeled. By СВАН program there are determined phase speed and attenuation factor.

Mathematical modeling of canal waves propagation in elastic seams was dealt with  at theMoscowmining institute under the supervision of V.S. Yamshchikov. The model was a flat-parallel layer bordering on the homogeneous half-spaces.

A lot of researchers dealt with calculating theoretical seismograms for different models [3, 4], and in these calculations there were obtained seismograms of Love waves for the models of one and two homogeneous layers bedding on a homogeneous half-space. Base on their analysis there was shown that with increasing the distance the visible frequency decreases, the amplitude of the wave process rounding attenuates. However, from the point of view of the process modeling Love waves propagation in the coal seam there can be noted a number of disadvantages of the abovementioned works. The models considered are in a small extent  brought to the real conditions of the wave field behavior before and after the breaking. There were not given criteria of detecting the coal seam breaking  and its type, there was no solution for the tear wave guides.

Due to the difficulty of obtaining the wave field in the models with breaking, at present many works are devoted to physical modeling. In them based on modeling, there is shown the possibility of separating coal seams tectonic breakings and that with the fault amplitude of the weaker wave guide there is impossible to separate the breakings. The authors prove that there are exist the waves which pass along  the seam, as well as the possibility of such reflected waves; there is presented the dependence of the reflected weave amplitude on its frequency. The studies revealed the mismatch of the registered wave spectrum maximum with the group speed minimum, and its practically independent frequency position on longitudinal waves speed in the wave guide and the enclosing medium.

From the works on physical modeling it’s necessary to separate studies [5]. In them there is given a description of interferential wave Pl (it is corresponded by the first wave tandem in a seismogram), propagating in a solid layer with a decreased speed. There is noted the intensity of the wave oscillation when locating the source and inside the layer. In work [5] there were studied the laws of interferential waves propagation on models of flat-parallel, curved and tear wave guides.

Physical modeling shows that all the parameters of canal waves are connected with the wave guide structure, with the enclosing medium characteristics and the conditions of carrying out the work.

In work [1] when studying on solid two-models with openings there was established a dependence of energy focusing on the ratio of the wave guide width and the wave length. There was noted a normal dispersion of the waves. The distances obtained between the energy maximums inside the wave guide coincide with the ones calculated by the formula of L.M. Brekhovskikh.

In spite of great possibilities of the physical modeling methods on three-dimension models and mathematical method of studying interferential waves propagation in coal seams (wave guides), a lot of important for practice questions are left uninvestigated. This is explained by a very approximate character of the real modeling, complicated in hypsometric relation and by the character of the coal seam breaking consisting in strongly changeable lithologic enclosing rocks.

Making a conclusion for the given analysis of the methods of experimental and theoretical modeling canal waves propagation process, we can formulate the main principles of improving the methods of modeling canal waves propagation:

– determining geological tear breakings using canal waves of Love and Relay type;

– a more detailed studying of the group speed and interferential waves amplitudes dependence on the types of the coal seam breakings;

– using canal waves phase and group speed dispersion defined by the structure of the wave guide and enclosing medium;

– developing a methodology of forecasting the coal-and-rock mass breaking for thin and middle coal seams and for the first (fundamental) mod, using the methodology for thick seams.

Realizing these principles is supposed to be carried out in the following sequence:

– modeling the process of the wave package propagation in the coal-and-rock mass;

– determining information parameters of amplitude breaking revealing no less than 0,5 of the cola seam thickness;

– determining seismic acoustic criteria of identifying amplitude tectonic breakings no less than half the coal seam thickness;

– approbation of the results obtained.

References

1. Кеilis-Birok V.I. Waves interferential surfaces. – М., 1965. – 195 p.

2. Levshin A.L. Surface and canal seismic waves. – М., 1973. – 176 p.

3. Krey T. Jn Seam seismic exploration techniques // Intern-coal exploration  sump-London, 1976. – Р. 29.

4. Аntsferov A.V., Zhulyabin V.I., Sleptsov V.A., Yastrebov V.V. Love and Relay waves dispersion in cola seams of the Moscow basin // Izv.vuzov, ser. «Geology and exploring». – 1980.  –  № 3. - P. 157-159.

5. Gilberstein P.G., Gurvich I.I., Pochtovik V.S. Model studies of two-dimension seismic wave guide with sharp boundaries // Izv. Of USSR AS, Earth physics. – 1966. – № 12. – P. 11-27.