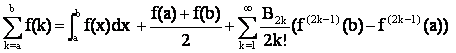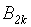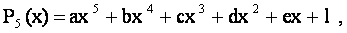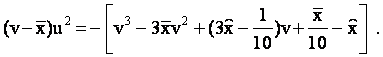ФОРМУЛА ЭЙЛЕРА-МАКЛОРЕНА В ТЕОРИИ СКОЛЬЗЯЩЕГО УСРЕДНЕНИЯ
ФОРМУЛА ЭЙЛЕРА-МАКЛОРЕНА В ТЕОРИИ СКОЛЬЗЯЩЕГО УСРЕДНЕНИЯ
Научная статья
Агранович Ю.Я.¹, Концевая Н.В.²
¹Воронежский государственный технический университет, Воронеж, Россия
²Финансовый университет при Правительстве РФ, Москва, Россия
Аннотация
В данной работе решена задача минимизации невязки в формуле Эйлера-Маклорена. Решение используется для определения параметров окна скользящего суммирования в сглаживании временных рядов. Приведены результаты численных экспериментов.
Ключевые слова: сглаживание, скользящее усреднение, оптимизация интервала, кубическая кривая.
Keywords: the smoothing of time series, sliding averaging, interval optimization, a cubic curve.
Сравнительная простота в использовании методов скользящего усреднения определяет основные недостатки их адекватного применения. Результаты сглаживания зависят в первую очередь от размера интервала усреднения и, во-вторых, собственно, от самого метода. В [1, 2] был разработан метод для определения весовых коэффициентов при усреднении , включающий параметр, который может варьироваться в зависимости от того, какие члены ряда желательно учитывать с большим весом, что способствует устойчивости процедуры обработки ряда [1, с. 71-76].
В данной работе ставится задача определения оптимального интервала усреднения, основанная на формуле Эйлера-Маклорена. Такой подход позволил проводить скользящее усреднение при изменяющемся окне усреднения, исключая субъективные моменты в выборе размера интервала сглаживания.
Рассмотрим формулу суммирования, связывающую частные суммы ряда с интегралом и производными его общего члена:
И зададимся следующей задачей: будем искать такой интервал интегрирования, когда невязка обращается в нуль, т.е. чтобы сумма значений функции в целых точках была равна интегралу от функции на рассматриваемом интервале. Иными словами, в формуле Эйлера-Маклорена мы будем считать величиной невязки сумму с числами Бернулли. В численных методах такое соотношение известно как формула прямоугольников для приближенного вычисления интегралов.
Можно показать, что для четных степеней полинома остаток, вообще говоря, отличен от нуля и задача имеет лишь, в некотором смысле, «ограниченные» решения, Однако для многочленов нечетных степеней это не так. Здесь появляется возможность выбирать сколь угодно большие длины интервала усреднения. Неожиданная роль в решении появляется у арифметических средних значений симметрических многочленов от корней исходного многочлена. Так, для многочлена 5-й степени:
Решение определяет некоторую кубическую кривую следующего вида:
Здесь: 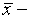 среднее арифметическое корней исходного многочлена;
среднее арифметическое корней исходного многочлена; 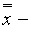 среднее арифметическое попарных произведений корней;
среднее арифметическое попарных произведений корней; 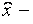 среднее арифметическое произведений по три.
среднее арифметическое произведений по три.
В качестве исходной базы были выбраны следующие исторические данные: дневные котировки (цены открытия) валютного курса USD/JPY за 200 дней на разных временных интервалах. Исследование данного метода скользящего усреднения включало следующие этапы:
- Для исходных данных рассчитываются аппроксимирующий полином пятой степени, параметры которого определяются МНК.
- Используя коэффициенты полученного полинома, определяются параметры кубической кривой, отображающей связь между центром интервала усреднения и размером интервала.
- В дальнейшем, используя полученную кубическую кривую, можно выбирать как номограмму оптимальные центр интервала и собственно ширину интервала сглаживания.
- Используя переменную ширину окна усреднения, производится процедура выравнивания временного ряда.
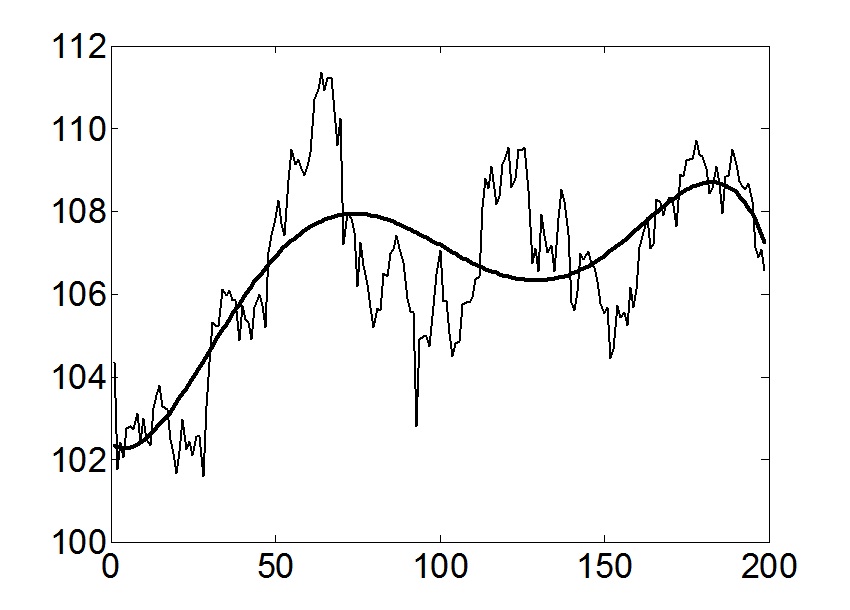
Данная задача была реализована в пакете MATLAB. На первом рисунке представлены результаты моделирования исходного временного ряда полиномом 5-ой степени.
Рис.1. Аппроксимация исходного ряда полиномом пятой степени
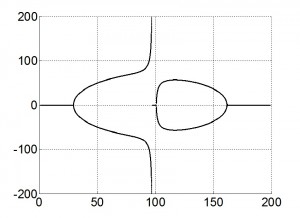
На рис.2 представлена кубическая кривая, определяющая размер окна сглаживания в зависимости от центра интервала. На горизонтальной оси – номер наблюдения (порядковый номер дня), по вертикальной оси изображен размер половины ширины интервала усреднения.
Рис.2. Ширина интервала сглаживания в зависимости от центра интервала
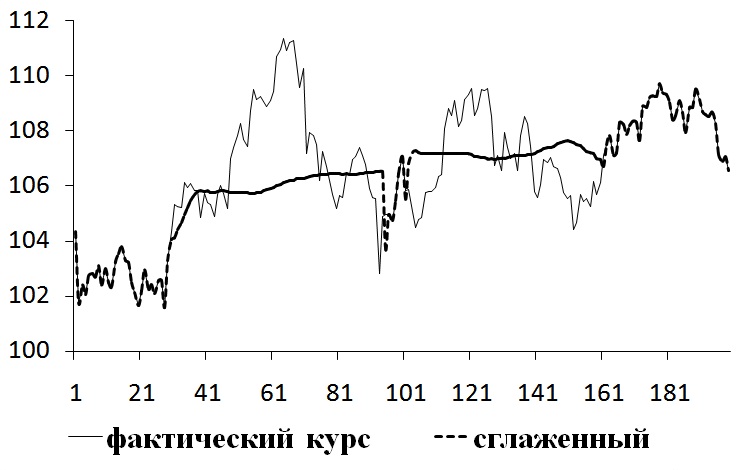
На заключительном этапе исследования проведено сглаживание исходного ряда с изменяющимся окном усреднения. На рис.3 представлены исходный временной ряд и сглаженный с помощью разработанного метода.
Рис.3. Исходный ряд и результаты сглаживания
Метод скользящего усреднения с изменяющимся окном сглаживания позволяет абстрагироваться от значительных изменений в середине ряда за счет увеличения размера окна сглаживания и максимально точно отобразить динамику крайних уровней. Вместе с тем, полученный сглаженный ряд отображает общее направление динамики процесса и может быть использован как для повторения предлагаемой процедуры, так и для возможного моделирования динамики. Например, аппроксимация полученного ряда с помощью полинома пятой степени становится более существенной (коэффициент детерминации увеличивается с 0,57 до 0,88).
При выявлении, в результате сглаживания, объективных закономерностей, информация о них может быть использована во многих областях: при обосновании управленческих решений, при планировании на микро и макроэкономических уровнях, при оценке ожидаемой доходности инвестиций и пр.
Список литературы / References
- Агранович Ю.Я. и др. Метод многоугольных чисел в процедуре сглаживания временных рядов и приложения к исследованию финансовых рынков / Ю.Я. Агранович, Н.В. Концевая, В.Л. Хацкевич // Экономика и математические методы, т. 46; вып.3 (2010), с. 71-81.
- Агранович Ю.Я. и др. Сглаживание временных рядов показателей финансовых рынков на основе многоугольных чисел / Ю.Я. Агранович, Н.В. Концевая, В.Л. Хацкевич // Прикладная эконометрика, № 3 (19) 2010, с.3-8.
- Агранович Ю.Я., Концевая Н.В. Метод определения параметров сглаживания временных рядов на основе минимизации невязки в формуле Эйлера-Маклорена // Современная экономика: проблемы и решения, № 7(19) 2011, с. 131-137.