АНАЛИЗ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ШЕСТЕРНИ ТЯГОВОГО РЕДУКТОРА ЛОКОМОТИВА 2ТЭ10Л
АНАЛИЗ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ШЕСТЕРНИ ТЯГОВОГО РЕДУКТОРА ЛОКОМОТИВА 2ТЭ10Л
Научная статья
Вельгодская Т.В.¹, Иванов В.В.², Гаджиев И.А.³
1, 2, 3 Омский государственный университет путей сообщения, Омск, Россия
Аннотация
Одним из высоконагруженных элементов колесно-моторного блока локомотива является шестерня тягового редуктора, передающая значительный вращающий момент от двигателя. Согласно «Стратегическим направлениям научно-технического развития ОАО «Российские железные дороги на период до 2015 г.», утвержденным президентом ОАО «РЖД» 30.08.2007, предполагается увеличение нагрузки на ось до 25-27 тс и повышение скорости движения поездов до 120 км/ч.[1] Таким образом, требования к ресурсу колесно-моторного блока непрерывно возрастают.
Ключевые слова: шестерня, напряженно-деформированное состояние, тяговый редуктор
Key words: gear, stress-strain state
Тяговая шестерня представлена в виде детали из стали 20ХН3А (рис. 1).

Рисунок 1 - Шестерня тягового редуктора
Основные механические характеристики стали представлены в табл. 1.
Таблица 1
Основные механические свойства стали
|
Механическая характеристика |
Значение |
| Плотность, кг/ |
7850 |
| Предел прочности, МПа |
1270 |
| Предел текучести, МПа |
1080 |
| Предел усталости, МПа |
540 |
| Модуль упругости, МПа |
210 000 |
| Коэффициент Пуассона |
0,3 |
Геометрические параметры тяговой шестерни редуктора представлены в табл. 2.
Таблица 2
Основные параметры шестерни
|
Параметр |
Значение |
| Число зубьев |
17 |
| Модуль, мм |
10 |
| Угол исходного контура, град |
20 |
| Коэффициент коррекции |
0,505 |
| Длина общей нормали, мм |
79,637 |
| Диаметр окружности выступов, мм |
198,88 |
| Передаточное число |
4,412 |
| Межцентровое расстояние, мм |
468,8 |
| Длина зуба, мм |
140 |
Необходимые для расчета характеристики тягового электродвигателя приведены в табл. 3.
Таблица 3
Основные характеристики тягового электродвигателя
|
Параметр |
Значение |
| Мощность, кВт |
305 |
| Номинальная частота вращения, об/мин |
585 |
| Максимальная частота вращения, об/мин |
2230 |
Моделирование напряженно–деформированного состояния производится на основе расчета геометрических параметров пятна контакта на поверхности зубьев шестерни и колеса. Определение параметров основано на решении задачи Герца для двух цилиндров. Расчет параметров пятен контакта описывается математической моделью (1) – (10).
Определим угловую скорость ω1 и ω2, c-1:
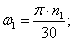 |
(1) |
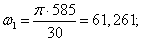 |
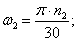 |
(2) |
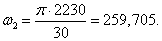 |
где n1 и n2 – номинальная и максимальная частоты вращения соответственно, об/мин.
Определим момент на валу T1 и T2, Нм:
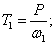 |
(3) |
где P – мощность тягового электродвигателя, Вт.
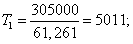 |
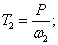 |
(4) |
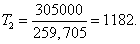 |
Определим нормальную силу F1 иF2 , Н:
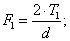 |
(5) |
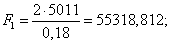 |
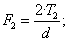 |
(6) |
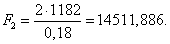 |
где d – делительный диаметр шестерни, м.
Определим ширину пятна контакта a1 и a2, мм:


| где R1 и R2 – радиусы приведенных цилиндров для зубьев шестерни и колеса соответственно, м; |
E1 и E2 – модули упругости материалов шестерни и колеса соответственно, Н/м2.
Максимальные контактные напряжения и , возникающие при сжатии двух цилиндров, МПа [3,4]:
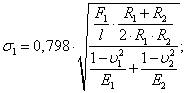 |
(9) |
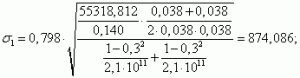 |
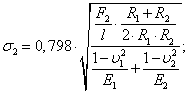 |
(10) |
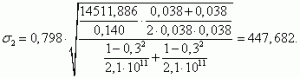 |
В системе трехмерного моделирования «КОМПАС» создана модель, являющаяся прототипом исследуемого объекта (рис. 2).

Рисунок 2 - Модель шестерни тягового редуктора
При исследовании напряженно–деформированного состояния шестерни тягового редуктора использовался метод конечных элементов, который дает возможность достаточно полно учесть геометрические формы и реальные условия работы передачи, распределение внешних нагрузок, а также физические свойства используемых материалов.
Разбиение шестерни на конечные элементы производится в соответствии со стандартным алгоритмом тетраэдризации [2, c. 308 – 312]. Трехмерная твердотельная модель шестерни разбивается на 364761 конечных элементов. Количество узлов – 544029, а число степеней свободы составляет 1612953. Результаты разбиения представлены на рисунке 2.
Для получения наиболее точных результатов выполнялось уплотнение сетки конечных элементов в зоне пятна контакта до 0,1 мм, а по рабочей поверхности зуба до 2 мм (рис. 3).

Рисунок 3 - Трехмерная модель шестерни с нанесенной сеткой конечных элементов
Определение напряжений, возникающих в шестерне, производились на ПЭВМ методом конечных элементов с помощью расчетного комплекса SolidWorks Simulation 2012, широко применяемого в настоящее время для решения инженерных задач. Моделирование напряженно-деформированного состояния производим для момента трогания локомотива, так как при этом возникают большие усилия.
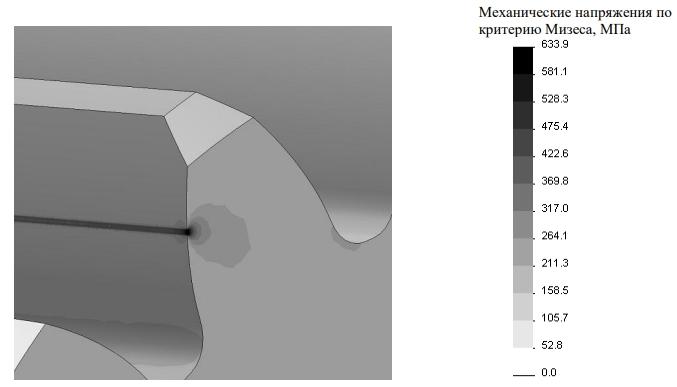
Рисунок 4 – Цветокодированное распределение механических напряжений в материале шестерни при зацеплении с колесом
Исходя из полученных результатов (рис 4.), можно сказать, что нагрузка распределяется по длине зуба неравномерно. Самые значительные напряжения возникают у краев зуба, а также у ножки зуба в месте сопряжения ее с зубчатым венцом.
Значения механических напряжений равные 633,9 МПа, полученные в результате моделирования, превышают допускаемые предел усталости (540 МПа) для выбранного материала. Таким образом, повышается риск возникновения и развития такого дефекта, как поверхностное выкрашивание (питтинг коррозия) металла в полюсной зоне. Кроме того, при моделировании принимались идеализирующие допущения, а в эксплуатации возникает перекос осей ведущей шестерни и колеса, что приводит к изменению формы пятна контакта и существенному увеличению значений механических напряжений. В дальнейшем планируется моделирование напряженно-деформированного состояния тяговой шестерни с учетом перекоса осей.
Список литературы / References
1. Гапанович В. А. Белая книга ОАО «РЖД»: Стратегические направления научно-технического развития компании / В. А. Гапанович // Железнодорожный транспорт. 2007. №8. С. 2 – 6
2. Галлагер Р. Метод конечных элементов. Основы: Пер. с англ. / Р. Галлагер. М.: Мир, 1948. 428 с.
3. Беляев Н. М. Сопротивление материалов / Н. М. Беляев. М: Наука, 1976. 608 с.
4. Беляев Н. М. Сопротивление материалов / Н. М. Беляев. М: Физматгиз, 1962. 856 с.
