АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ МНОГОЦЕЛЕВОЙ ЛИНЕЙНОЙ ОПТИМИЗАЦИИ С УЧЕТОМ ВЗАИМОДЕЙСТВИЯ ЦЕЛЕЙ
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ МНОГОЦЕЛЕВОЙ ЛИНЕЙНОЙ ОПТИМИЗАЦИИ С УЧЕТОМ ВЗАИМОДЕЙСТВИЯ ЦЕЛЕЙ
Научная статья
Аристова Е.М.
Воронежский государственный университет, Воронеж, Россия
Аннотация
В статье рассматривается многокритериальная задача линейного программирования. Предлагается алгоритм ее решения, учитывающий тип взаимодействия между целевыми функциями (кооперация, конфликт и независимость).
Ключевые слова: Задача линейной многоцелевой оптимизации, коэффициент взаимодействия целевых функций, принцип принятия группового решения, обобщенная целевая функция
Key words: Linear multi-purpose optimization problem, interaction factor of criterion functions, principle of adoption of the group decision, the generalized criterion function
Рассмотрим задачу линейной многоцелевой оптимизации следующего вида 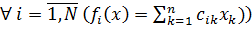 , где
, где
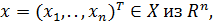
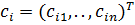 – вектор коэффициентов целевой функции.
– вектор коэффициентов целевой функции.
В линейном случае градиент каждой целевой функции (вектор, указы-вающий направление, в котором значение целевой функции 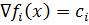 увеличивается) определяется коэффициентом целевой функции и представляет собой константу.
увеличивается) определяется коэффициентом целевой функции и представляет собой константу.
Коэффициент взаимодействия целевых функций определяется по формуле [2]:
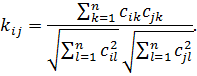
Рассмотрим теперь многоцелевую задачу линейного программирования из R2
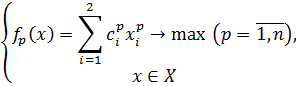
при 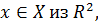 где X– множество допустимых значений x
где X– множество допустимых значений x
Предлагается следующий алгоритм решения такой задачи линейного программирования, учитывающий тип взаимодействия между целевыми функциями и основанный на использовании аддитивной свертки, которая позволяет для каждого подмножества целевых функций с определенным типом взаимодействия сформировать обобщенную функцию [1,2]:
- Для каждой целевой функции решить свою однокритериальную задачу, получив оптимальное решение и соответствующее значение целевой функции;
- Для каждой пары целевых функций определить коэффициент взаимодействия. Составить матрицу коэффициентов взаимодействия целевых функций.
- Определить тип взаимодействия между всеми парами целевых функций [2,3].
- Определить множества кооперирующих, конфликтующих и неза-висимых функций для каждой конкретной цели.
- Для целевой функции определить коэффициенты значимости соответствующего взаимодействия.
- Для выбранного принципа принятия группового решения [4] построить ранжирование решений по предпочтительности в зависимости от значений целевой функции.
- С помощью специальной процедуры на основе расстояний между множествами однокритериальных задач определить коэффициенты зависимости для каждой пары целевых функций.
- Построить оценки, используя функции из соответствующих множеств, с которыми конкретная целевая функция кооперирует, конфликтует и независима, и коэффициенты зависимости.
- Построить обобщенную целевую функцию.
- Решить задачу линейного программирования с исходными граничными условиями и построенной обобщенной целевой функцией.
В статье рассмотрена задача многоцелевой линейной оптимизации. Предлагается алгоритм решения такой задачи, основанный на учете типов взаимодействия между целевыми функциями и построении аддитивной свертки.
Список литературы / References
- Аристова Е.М. Об одном подходе к анализу задач многокритериальной оптимизации / Е.М. Аристова, Т.М. Леденева // Журнал «Системы управления и информационные технологии» Воронеж. гос. технич. ун-та. – Воронеж : ВГТУ, 2012. – №1(47). – С. 11-14.
- Мелькумова Е.М. Многокритериальная оптимизация на основе меры зависимости целевых функций / Е.М. Мелькумова // Известия Тульского гос. ун-та. Сер. Естественные науки. – Тула : ТулГУ, 2011. – выпуск №1. – С. 177-187.
- Мушик Э. Методы принятия технических решений / Э. Мушик, П. Мюллер. – М. : Мир, 1990. – 206 с.
- Робертс Ф. С. Дискретные математические модели с приложениями к социальным биологическим и экологическим задачам / Ф.С. Робертс. – М. : Наука, 1986. – 494 с.
