ВЫБОР КРИТЕРИЯ ДЛЯ РАЗДЕЛЕНИЯ ДЕРЕВЬЕВ ПО ФОРМЕ ПОПЕРЕЧНОГО СЕЧЕНИЯ СТВОЛА

Горошко А.А.¹, Вайс А.А.², Якунин М.А.³, Амельков А.А.⁴, Ушаков А.С.⁵, Седембиль Ш.А.⁶

¹Аспирант, Сибирский государственный технологический университет, ² ORCID:  0000-0003-4965-3670, Профессор, доктор cельскохозяйственных наук, Сибирский государственный технологический университет, ^{3, 4, 5, 6}Бакалавры, Сибирский государственный технологический университет

ВЫБОР КРИТЕРИЯ ДЛЯ РАЗДЕЛЕНИЯ ДЕРЕВЬЕВ ПО ФОРМЕ ПОПЕРЕЧНОГО СЕЧЕНИЯ СТВОЛА

Аннотация

Форма поперечного сечения ствола - малоизученный показатель, который отражает влияние природных условий на отдельное дерево и древостой в целом. В процессе определения формы возникает проблема выбора надежного критерия, характеризующего среднюю форму сечения для насаждения. Преобразованные исходные данные характеризуются выраженной правосторонней асимметрией, что затрудняет выбор такого критерия. В этом случае рекомендуется использовать среднее квадратическое отклонение как наиболее приемлемый и оптимальный показатель.

Ключевые слова: форма, поперечное сечение, критерий, диаметр.

Goroshko A.A.¹, Vajs A.A.², Jakunin M.A.³, Amel'kov A.A.⁴, Ushakov A.S.⁵, Sedembil' Sh.A.⁶

¹Postgraduate student, Siberian State Technoiogical University, ²Professor, PhD in Agriculture, Siberian State Technoiogical University, ^{3, 4, 5, 6} Bachelors, Siberian State Technoiogical University

SELECTION CRITERIA FOR THE SEPARATION OF TREES IN THE FORM OF CROSS-SECTION BARREL

Abstract

The sectional shape of the trunk - poorly known indicator, which reflects the impact of the natural environment on a single tree and forest stand as a whole. In the process of determining the shape of a problem choosing a reliable criterion that characterizes the average cross section shape for planting. The converted original data are characterized by a pronounced right-sided asymmetry, which complicates the choice of such a criterion. In this case, it is recommended to use the standard deviation as the most acceptable and optimal performance.

Keywords: shape cross-section, the criterion, diameter.

Форма поперечного сечения дерева, особенно на высоте 1,3 м, может существенно влиять на определение объема ствола и запаса насаждения.

В учебнике по лесной таксации М.М. Орлов [2] указывал на факторы, оказывающие влияние на форму поперечного сечения ствола дерева:

• древесная порода;
• возраст;
• часть дерева, для которого взято сечение;
• условия произрастания.

Для определения площади поперечного сечения используются две геометрические формулы: эллипс и круг. Эллипсовидная форма позволяет более точно определить площадь сечения, но и требует более сложных измерений. Для достижения наиболее точного результата площадь сечения необходимо вычислять по максимальному и минимальному диаметру по формуле эллипса.

Так же, при измерении диаметров растущих деревьев, кора будет оказывать влияние на определение формы и площади поперечного сечения. Толщина коры неодинакова у деревьев разных пород, а в пределах породы у деревьев разного возраста. Профессор В.Я. Добровлянский [3] указывал, что при определении поперечных сечений нижней части ствола по формулам круга и эллипса погрешность расчета возрастает с увеличением толщины коры. У деревьев с тонкой корой это преувеличение в среднем равно 1%, с толстой корой - 2-3%, с очень толстой - 4-5%. При определении площадей окоренных стволов формулы круга и эллипса дают для любого сечения по всей высоте ствола преувеличение на 0,5-1%.

Форма поперечного сечения ствола это фактор, отражающий воздействие природных условий на дерево. Данное исследование проводилось на основе 13 пробных площадей заложенных на территории заповедника «Столбы» Красноярского края. На каждой пробной площади были измерены диаметры у 100-150 деревьев сосны обыкновенной (Pínus sylvéstris). Для определения формы ствола замеры диаметров производились по сторонам света (с севера на юг, с запада на восток, с северо-запада на юго-восток и с северо-востока на юго-запад). Итого было сделано 4 замера у каждого дерева сосны. Измерения выполнялись с ошибкой до 0,1 см, точность опыта не превышала 5 %.

Измеренные диаметры сами по себе не позволяют оценить форму ствола. Для этого использовались абсолютные отклонения от среднего диаметра. Чтобы исключить влияние абсолютных значений размеров деревьев на определение формы, было решено выразить отклонения в процентах от среднего диаметра, который определялся как средний по четырем сторонам (формула 1). Пример расчета представлен в таблице 1.

 ,                                     (1) где   – отклонения, %;  – диаметр, см;  – средний диаметр, см.  

Таблица 1 – Пример расчета отклонений

№ дерева	Диаметр, см				Средний диаметр, см	Отклонения, %
	С-Ю	З-В	СЗ-ЮВ	СВ-ЮЗ		С-Ю	З-В	СЗ-ЮВ	СВ-ЮЗ
1	41,4	49,3	45,8	45,7	45,6	9,11	8,23	0,55	0,33
2	33	33,5	32	34,3	33,2	0,60	0,90	3,61	3,31
3	38,3	38,5	37,9	37,5	38,1	0,66	1,18	0,39	1,45
4	43	41,8	41,6	44,9	42,8	0,41	2,39	2,86	4,85

 

Полученные результаты по четырем сторонам для каждого дерева позволяют судить о форме поперечного сечения ствола. Соответственно, чем больше отклонение, тем более неправильную форму сечения имеет ствол. Исследуя множества деревьев на участке, произрастающих в одинаковых лесорастительных условиях, можно судить о наиболее типичной форме ствола для данной местности и в дальнейшем определить факторы влияния. Описательная статистика по отклонениям для исследуемых участков леса приведена в таблице 2.

 

Таблица 2 – Описательная статистика для исследуемых участков леса

Показатель	Номера участков
	1	2	3	4	6	7	8
Среднее	2,17	2,06	2,47	2,76	1,99	2,94	2,41
Стандартная ошибка	0,09	0,07	0,11	0,10	0,08	0,13	0,11
Медиана	1,78	1,72	2,08	2,11	1,55	2,13	1,82
Мода	1,95	1,05	2,08	0,00	0,00	0,00	0,00
Стандартное отклонение	1,83	1,48	1,95	2,25	1,72	2,62	2,20
Эксцесс	5,09	0,71	1,64	1,19	7,91	2,93	7,21
Асимметричность	1,71	0,95	1,24	1,17	1,96	1,59	2,04
Минимум	0,00	0,00	0,09	0,00	0,00	0,00	0,00
Максимум	12,74	7,59	11,45	11,76	14,84	14,55	16,38
Счет	460	432	304	488	420	424	416

  Продолжение таблицы 2

Показатель	Номера участков
	9	10	11	12	13	14
Среднее	2,82	2,44	2,50	2,85	2,23	2,76
Стандартная ошибка	0,10	0,09	0,09	0,11	0,09	0,11
Медиана	2,35	1,94	2,09	2,37	1,78	2,28
Мода	3,27	0,78	0,00	0,66	1,51	0,00
Стандартное отклонение	2,06	2,04	1,87	2,23	1,80	2,23
Эксцесс	1,02	2,95	1,45	2,37	3,07	2,75
Асимметричность	1,00	1,56	1,11	1,23	1,42	1,37
Минимум	0,00	0,00	0,00	0,00	0,00	0,00
Максимум	11,66	12,08	11,72	15,41	12,12	14,34
Счет	428	484	404	452	396	416

 

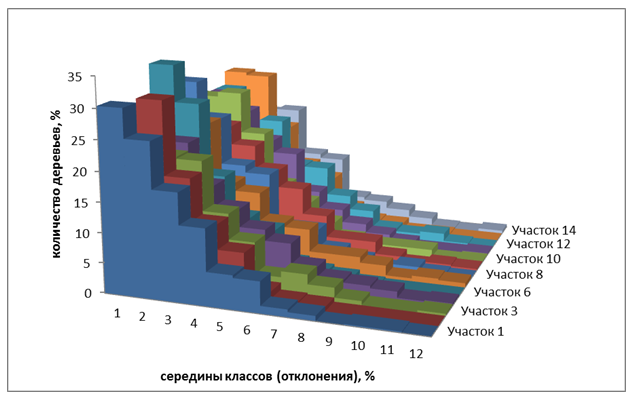
Из таблицы 2 видно, что среднее значение выборки по всем участкам изменяется от 1,99 до 2,85 %. Асимметричность колеблется от 0,95 до 2,04, эксцесс от 0,71 до 7,91. Оба показателя больше нуля, значит, распределение имеет правостороннюю асимметрию и выраженную эксцессивность[1]. Исходя из этого, можно утверждать, что оно не соответствует закону нормального распределения. Гистограмма изменения среднеквадратической величины (отклонений) представлена на рисунке 1.

Рисунок 1 – Распределение среднеквадратической величины

На следующем этапе решается задача выявления показателя, характеризующего распределение на каждом участке. Среднее значение обладает наибольшей устойчивостью. Но в данном случае мы имеем дело со случайными величинами, имеющими распределение с выраженной правосторонней асимметрией. Поэтому возможно применение разных видов средних. Исходя из этого, по каждому участку было рассчитано несколько видов средних величин (арифметическое, квадратическое, геометрическое и медиана), их расчеты представлены в таблице 3.

Таблица 3 – Средние величины

Виды средних	Номера участков
	1	2	3	4	6	7	8
Среднее арифметическое	2,17	2,06	2,47	2,76	1,99	2,94	2,41
Среднее квадратическое	2,84	2,53	3,14	3,56	2,63	3,94	3,26
Среднее геометрическое	1,20	1,24	1,70	1,36	0,91	1,52	0,80
Медиана	1,78	1,72	2,08	2,11	1,55	2,13	1,82

  Продолжение таблицы 3

Виды средних	Номера участков
	9	10	11	12	13	14
Среднее арифметическое	2,25	1,76	1,27	1,90	1,47	1,89
Среднее квадратическое	2,31	2,18	1,59	2,36	1,91	2,27
Среднее геометрическое	2,19	0,00	0,00	0,01	0,01	0,01
Медиана	2,08	1,74	1,23	1,82	1,31	2,04

 

Как видно из таблицы 3 для всех средних соблюдается свойство мажорантности (среднее квадратическое > среднее арефметическое > среднее геометрическое). На всех участках медиана меньше среднего арифметического, что подтверждает гипотезу о правосторонней ассиметрии.

Для характеристики формы деревьев в насаждении нами был выбран критерий - среднее квадратическое значение (формула 2).

 ,                                             (2) где  – среднее квадратическое, %;  – отклонение, %; n – объем выборки, шт. Среднее квадратическое по всем участкам составило 3,2 %. Отклонения, возведенные во вторую степень, сглаживают резкую правостороннюю асимметрию. Кроме того, необходимо руководствоваться физическим смыслом средней величины. Средние значения рассчитываются по отклонениям, таким образом, для дерева диаметром 30 см 3% будут составлять 0,9 см, а для 60 см – 2 см. Меньшие средние величины будут отражать слишком незначительные изменения диаметра.

Заключение:

• При выборе среднего для характеристики асимметричных распределений целесообразно использовать среднее квадратическое значение.
• Отклонения, возведенные в квадрат, делают распределение менее ассиметричным. Учитывая физический смысл, средняя квадратическая величина является оптимальным критерием для определения формы сечения ствола.
• Результаты исследований позволили считать величину 3 % оптимальным критерием различия при разделении деревьев по форме поперечного сечения на высоте 1,3 м (округлая, эллипсовидная, неправильная).

Литература

1. Мятлев В.Д. и др. Теория вероятностей и математическая статистика. Математические модели / В.Д. Мятлев, Л.А. Панченко, Г.Ю Ризниченко, А.Т. Терехин. – М.: Издательство Академия, 2009. – 320 с.
2. Орлов, М.М. Лесная таксация: 3-е изд / М.М. Орлов. - Ленинград: Лесное хоз-во и лесн. пром-ть. - 1929. - 532 с.
3. Добровлянский, В.Я. К вопросу об определении объема срубленных деревьев / В.Я. Добровлянский // Известия лесного института. - В.13. - 1915. - с. 24-30.

References

1. Myatlev V.D. i dr. Teoriya veroyatnostej i matematicheskaya statistika. Matematicheskie modeli / V.D. Myatlev, L.A. Panchenko, G.Yu Riznichenko, A.T. Terexin. – M.: Izdatel'stvo Akademiya, 2009. – 320 s.
2. Orlov, M.M. Lesnaya taksaciya: 3-e izd / M.M. Orlov. - Leningrad: Lesnoe xoz-vo i lesn. prom-t'. - 1929. - 532 s.
3. Dobrovlyanskij, V.Ya. K voprosu ob opredelenii ob"ema srublennyx derev'ev / V.Ya. Dobrovlyanskij // Izvestiya lesnogo instituta. - V.13. - 1915. - s. 24-30.