СВЕРХМОЩНОЕ ПОЛУДИПОЛЬНОЕ СВЧ МАГНИТНОЕ ПОЛЕ КОМПАКТНОЙ ФОРМЫ В СВЕРХМАЛОМ ОБЪЁМЕ ПРОСТРАНСТВА
Леонов Ю.В.
Частные исследования, Частное финансирование
СВЕРХМОЩНОЕ ПОЛУДИПОЛЬНОЕ СВЧ МАГНИТНОЕ ПОЛЕ КОМПАКТНОЙ ФОРМЫ В СВЕРХМАЛОМ ОБЪЁМЕ ПРОСТРАНСТВА
Аннотация
В статье описана физическая модель полу дипольного СВЧ магнитного поля, которое было получено при работе со сверх высокими частотами, и которое открывает перспективу использования высоко эффективных, сверх мощных и сверх компактных электротехнических компонентов-источников магнитного поля, при их весьма скромных габаритах, и при их малых индуктивных характеристиках, а так же позволяет использовать новые методы управления резонансными процессами в специальных колебательных контурах..
Ключевые слова: СВЧ (сверх высокая частота), магнитное поле, диполь, электромагнитная индукция, взаимоиндукция, индуктивность, индуктивное сопротивление, самоиндукция, переменный ток, компактность, миниатюризация.
Leonov Y.V.
Private research, Private financing
COMPACT SUPER-POWERFUL AND SEMI-DIPOLE SHF MAGNETIC FIELD IN ULTRA-SMALL SPACE VOLUME
Abstract
The article describes the physical model of the semi-dipole SHF magnetic field that has been developed while working with super high frequencies. Such field will allow to use highly efficient, super-powerful and ultra-compact electrical components that are the sources of magnetic field. It should be noted, that these components are rather small in size and have low inductive properties. Also, the field makes it possible to apply new methods of controlling resonance processes within the specific oscillating circuit.
Keywords: SHF (super high frequency), magnetic field, dipole, electromagnetic induction, interinduction, inductance, inductive resistance, self-induction, alternate current, compactness, miniaturization.
В прошлой статье «ФИЗИЧЕСКАЯ МОДЕЛЬ ИНДУКТИВНОСТИ» в «Международном научно-исследовательском журнале» [Выпуск №11(42) 2015 Часть 3 Декабрь (стр. 18) – Электронный Архив номеров: 5015 Декабрь 11-3(42)], были рассмотрены основные свойства индуктивности и сформулирована её физическая модель. Безусловно, полученная физическая модель индуктивности, дала очень много для понимания других сопряжённых физических процессов, но так же, она ещё и позволила выйти, на новые технические решения использования магнитного поля. В этой статье, соленоид [1], на основе которого формулировалась физическая модель индуктивности, будет рассмотрен, теперь уже, с точки зрения связи пространственной формы магнитного поля, которое он генерирует, с характеристиками переменного тока, проходящего через него.
Пространственная форма магнитного поля соленоида.
В настоящее время, практически все соленоиды генерируют магнитное поле такой формы, какая показана на Схеме 1.
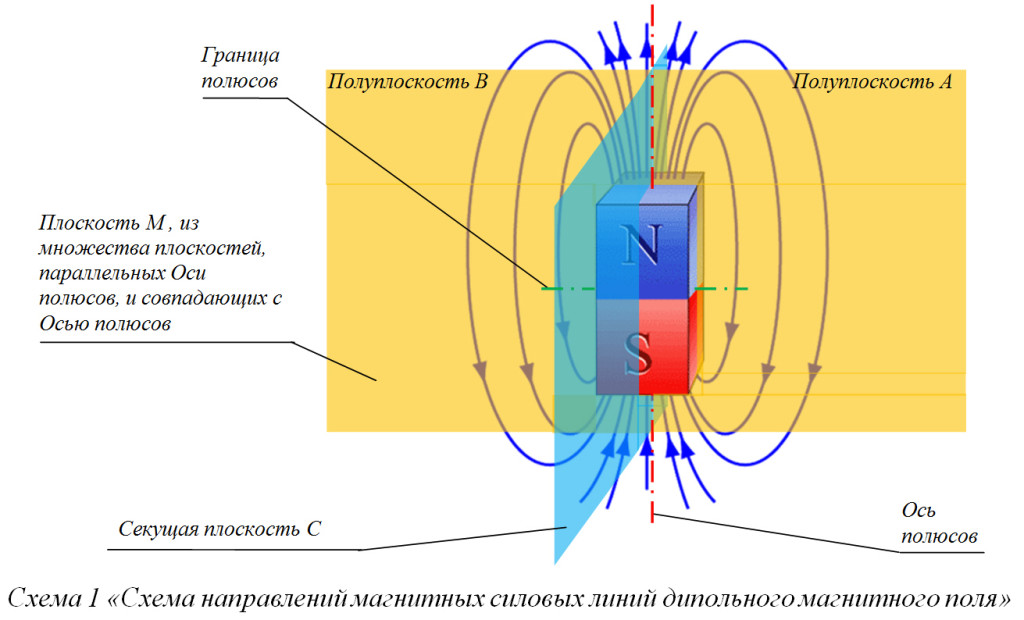
Обозначим данную форму магнитного поля – дипольной. Рассмотрим поближе эту форму магнитного поля. Данное дипольное магнитное поле имеет характерную схему направлений магнитных силовых линий, при рассмотрении его во множестве плоскостей, параллельных Оси полюсов[2] магнитного поля, и совпадающих с Осью полюсов этого магнитного поля – обозначим эти плоскости, как Осевые плоскости[3]. Возьмём любую Осевую плоскость из множества Осевых плоскостей, и обозначим её – Осевая плоскость М. Рассечём эту Осевую плоскость М, любой ортогональной Секущей плоскостью С, строго по Оси полюсов. Результатом разделения Осевой плоскости М, станет получение двух Полуплоскостей Осевой плоскости М, которые, в свою очередь, обозначим, как Полуплоскость А и Полуплоскость В. Теперь можно убедиться, что силовые линии дипольного магнитного поля, в полученных Полуплоскостях А и В, имеют разное направление – то есть, магнитные силовые линии направлены по часовой стрелке в Полуплоскости А дипольного магнитного поля, и против часовой стрелки в Полуплоскости В дипольного магнитного поля. Именно данная структура дипольного магнитного поля обуславливает наличие, у соленоида-источника этого дипольного магнитного поля, характерного физического свойства «индуктивность», со всеми, присущими ей, признаками и свойствами, которые подробно, были описаны и рассмотрены в прошлой статье «ФИЗИЧЕСКАЯ МОДЕЛЬ ИНДУКТИВНОСТИ».
Пространственная форма магнитного поля прямого проводника с током.
Теперь рассмотрим пространственную форму магнитного поля прямого проводника с током в Схеме 2.
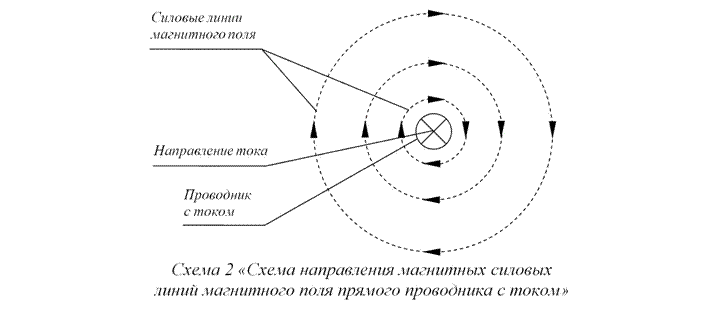
Если теперь сравнить структуру силовых линий дипольного магнитного поля соленоида в Полуплоскости А на Схеме 1, и структуру силовых магнитных линий прямого проводника с током на Схеме 2, то станет вполне очевидным то, что они совершенно идентичны (см. Схему 3).
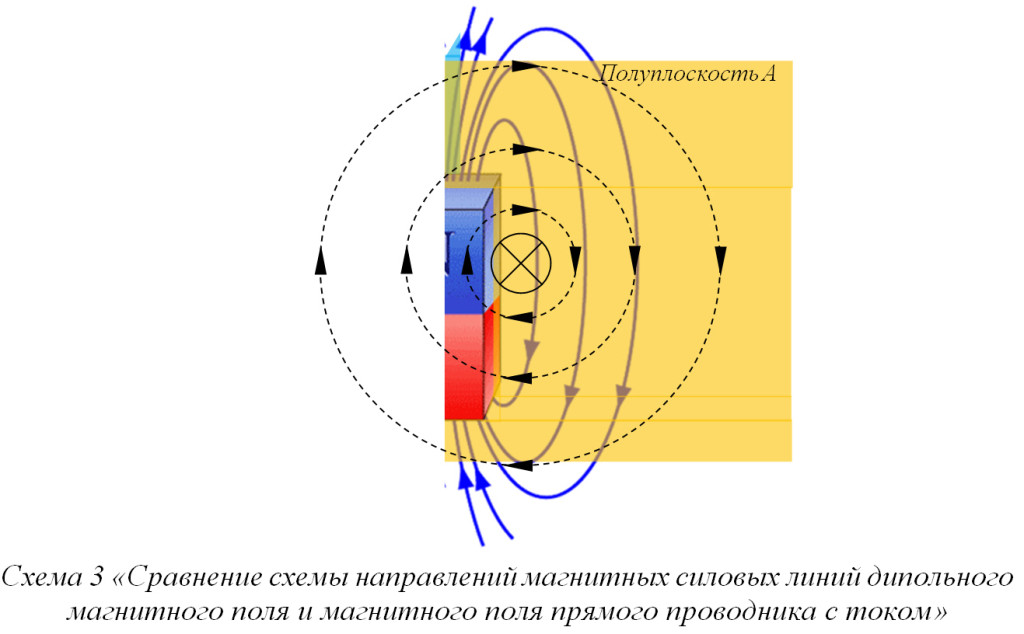
Вследствие того, что магнитное поле прямого проводника с током, по сути, является ничем иным, как половиной дипольного магнитного поля соленоида, то обозначим магнитное поле прямого проводника с током, как полудипольное.
Взаимосвязь частоты переменного тока в соленоиде, с пространственной формой его магнитного поля
Итак, есть ли взаимосвязь пространственной формы магнитного поля соленоида, с частотой переменного тока, на котором он работает? Безусловно, есть. Для того, что бы убедится в этом, необходимо вспомнить из прошлой статьи подробное описание процесса протекания переменного тока в соленоиде (см. статью «ФИЗИЧЕСКАЯ МОДЕЛЬ ИНДУКТИВНОСТИ», в т.ч. Схему 2 и Схему 3). Далее, что бы понять, как соленоид генерирует дипольную форму магнитного поля, необходимо, с учётом материала прошлой статьи, обратить внимание на один, казалось бы, несколько неприметный фактор – если соотнести частоту, на которой обычно работают соленоиды (в готовых электрических машинах, в виде, уже готовых, электротехнических компонентов), с эквивалентной[4] электромагнитной волной (далее по тексту – ЭМВ), то совсем не трудно убедиться, что, как правило, длина, или всего проводника рассматриваемого многовиткового соленоида, или проводника одного полного витка[5] одновиткового соленоида, в своём геометрическом выражении, не просто меньше длины полной (полного периода) λ эквивалентной ЭМВ, а даже на много меньше ½ (одного полупериода) длины полной λ эквивалентной ЭМВ. Именно этот, вроде бы, несущественный фактор, и обуславливает формирование соленоидом магнитного поля, исключительно, дипольной формы, а значит, обуславливает и наличие в этом соленоиде, всех характерных свойств индуктивности. Теперь, сформулируем условие работы соленоида, когда он будет формировать дипольную форму магнитного поля (см. Схему 1), через геометрическую длину проводника соленоида (см. статью «ФИЗИЧЕСКАЯ МОДЕЛЬ ИНДУКТИВНОСТИ», в т.ч. Схему 2 и Схему 3) и геометрическую длину λ эквивалентной ЭМВ, в двух выражениях, когда длина λ эквивалентной ЭМВ, будет больше, или длины l проводника одного полного витка одновиткового соленоида, или длины l
всего проводника многовиткового соленоида, в два раза и более:
а – для случая с одновитковым соленоидом –
λ
= l *2*n (при 
=
) Формула 1.1
в – для случая с многовитковым соленоида, с учётом взаимоиндукции между соседними витками –
λ = l*2*n (при =) Формула 1.2
где:
– частота переменного тока, проходящего через соленоид;
– частота эквивалентной ЭМВ;
λ – длина эквивалентной ЭМВ;
l – длина проводника одного полного витка одновиткового соленоида;
l – полная длина проводника, составляющего все витки многовиткового соленоида;
n – любое число, из множества натуральных чисел ;
2 – коэффициент полупериода – определяет условие, что полная длина проводника одного полного витка одновиткового соленоида или полная длина всего проводника многовиткового соленоида, обязательно будет меньше или равна ½ λ – то есть, обязательно будет меньше или равна одному полупериоду эквивалентной ЭМВ;
Данное условие обеспечивает формирование магнитного поля дипольной формы соленоидом, и наличие у него всех признаков индуктивности.
Теперь, рассмотрим и сформулируем условие, когда длина λ эквивалентной ЭМВ, геометрически равна длине проводника одного полного витка В-1 рассматриваемого соленоида (см. Схему 4, Схему 5, Схему 6 и Схему 7):
λ =l (при =) Формула 2
где:
– частота переменного тока проходящего, через рассматриваемый соленоид;
– частота эквивалентной ЭМВ;
λ – длина эквивалентной ЭМВ;
l – длина проводника одного полного витка В-1 рассматриваемого соленоида;
При соблюдении условия Формулы 2, а так же, согласно правилам и принципам взаимоиндукции и магнитной индукции (которые здесь работают, уже внутри самого рассматриваемого соленоида), картина формирования магнитного поля, в рассматриваемом соленоиде, теперь уже будет такая, как показано на Схеме 4 и Схеме 5.
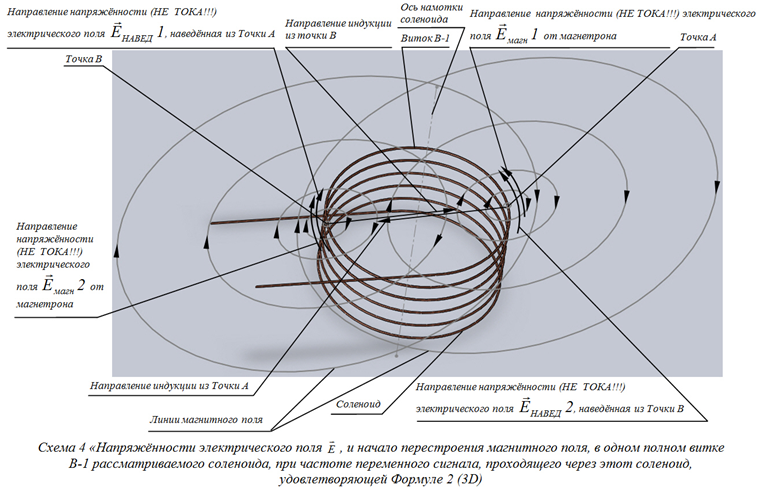
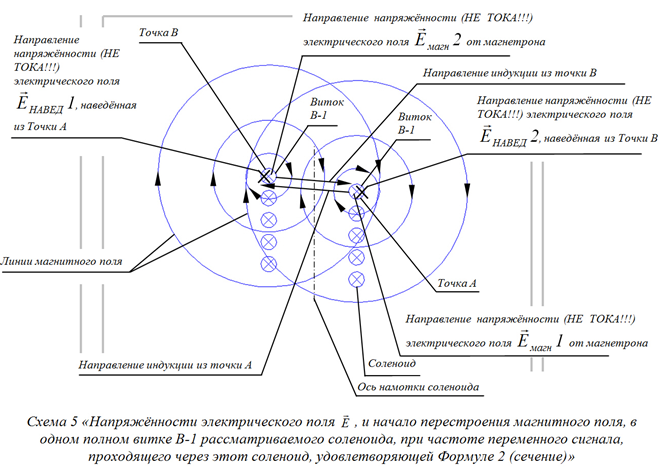
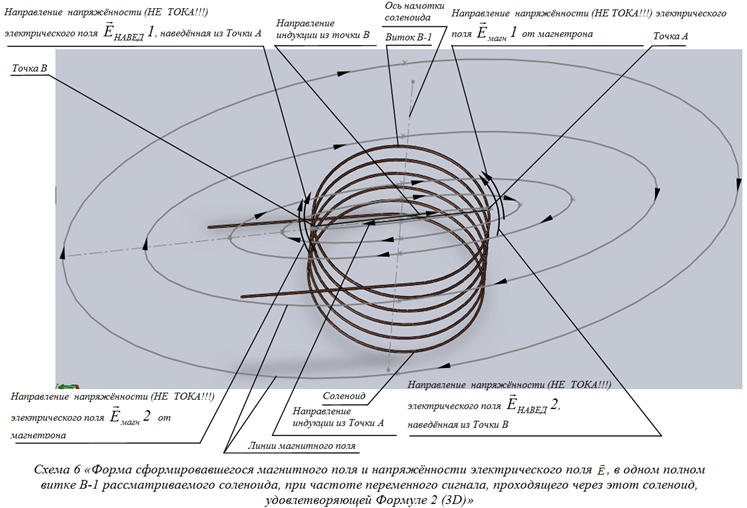
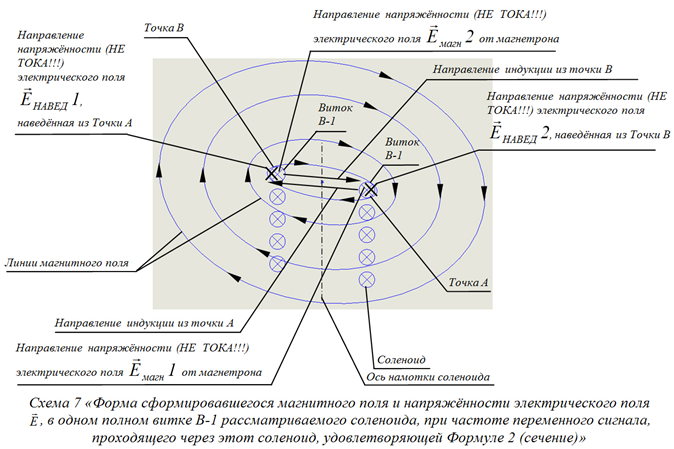
Окончательный же вид, сформированного магнитного поля в рассматриваемом соленоиде, при соблюдении условия Формулы 2, будет таким, как показано на Схеме 6 и Схеме 7.
Подобное физическое решение было получено в системе «СВЧ передатчик-приёмник», где передатчиком был магнетрон, а приёмником был маловитковой соленоид с активной нагрузкой (см. Схему 8).
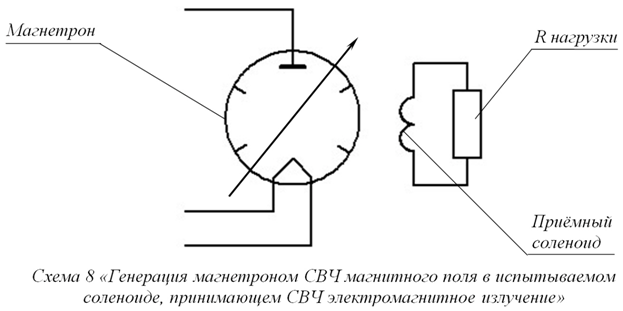
Физический механизм данного технического решения объясняется элементарно (см. Схему 4 и Схему 5). Обозначим один полный виток приёмного соленоида, как В-1. Когда магнетрон, в приёмном соленоиде, наводит основную напряжённость электрического поля 
, частота которой связана с длиной l проводника полного витка В-1 приёмного соленоида, удовлетворяя условию Формулы 2, то в точках А и В [6] (см. Схему 4 и Схему 5), взятых в любом месте полного витка В-1 приёмного соленоида генерируются напряжённости электрического поля 1 и 2, двух разных полупериодов одного полного периода фазы основного переменного сигнала от магнетрона – положительного и отрицательного. То есть, если в точке А, генерируется составляющая основной напряжённости электрического поля 1, положительного полупериода фазы основного переменного сигнала от магнетрона, то в точке В, обязательно генерируется составляющая основной напряжённости электрического поля 2, отрицательного полупериода фазы основного переменного сигнала от магнетрона, и наоборот... При этом, если магнетрон, в приёмном соленоиде, генерирует основной переменный сигнал с частотой, удовлетворяющей Формуле 2, то, согласно принципам магнитной индукции и взаимоиндукции, но уже внутри самого соленоида, основная напряжённость электрического поля 1 первого полупериода фазы основного переменного сигнала от магнетрона, из точки А, витка В-1, индуцирует в точке В, того же витка В-1, наведённую переменную напряжённость электрического поля 
1, касательный вектор которой, всегда направлен касательно к кривой, образованной проводником витка В-1, в ту же сторону, в которую направлен касательно к кривой, образованной проводником витка В-1, касательный вектор основной напряжённости электрического поля 2 второго полупериода фазы, того же основного переменного сигнала от магнетрона. Вдоль проводника, в этой же точке В, направления тех же 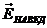1 и 2, теперь тоже совпадают. Аналогичная ситуация происходит и в точке А, но уже с 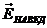2 и 1. 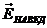Соответственно, 1 и 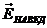2, уже не компенсируют 2 и 1, а раскомпенсируют и усиливают 2 и 1, в виду того, что при соблюдении условий Формулы 2, в одном витке В-1 приёмного соленоида, основная напряжённость электрического поля имеет, два разных полупериода фазы переменного сигнала от магнетрона, с двумя разными направлениями векторов своей напряжённости (см. Схему 6 и Схему 7). Данная форма магнитного поля, как видно из Схемы 6 и Схемы 7, очевидно, имеет такую же пространственную форму и структуру, как и полудипольная форма магнитного поля прямого проводника с током на Схеме 2 – это по праву позволяет утверждать, что магнитное поле соленоида, работающего на частоте, согласно Формуле 2, и полудипольное магнитное поле прямого проводника с током, безусловно, идентичны, что на полном основании, позволяет называть форму магнитного поля соленоида работающего на частоте, согласно Формуле 2, так же – полудипольной. Отмечено, что напряжённость магнитного поля соленоида, работающего на частоте, согласно Формуле 2, заметно превосходит расчётные показатели, вследствие чего, расчётная нагрузка «R нагрузки» (см. Схему 8), которая бралась с запасом по мощности, была полностью выведена из строя и разрушена. Само магнитное поле соленоида, работающего на частоте, согласно Формуле 2, имеет очень компактную и сконцентрированную пространственную форму. Так же замечено, что с ростом частоты, напряжённость магнитного поля, генерируемого приёмным испытываемым соленоидом, стремилась, то к своему максимуму, то к своему минимуму. Внимательно проанализировав следствия рассмотренных физических моделей на Схеме 4, Схеме 5, Схеме 6 и Схеме 7, можно с уверенностью утверждать, что условием максимума напряжённости магнитного поля, при увеличении частоты переменного тока, в рассматриваемом соленоиде, является наличие полудипольного магнитного поля и наличие нечётного количества полных длин λ эквивалентной ЭМВ, ровно и целиком, укладывающихся в проводнике полного витка В-1 рассматриваемого приёмного соленоида, а наличие дипольного магнитного поля и наличие чётного количества полных длин λ эквивалентной ЭМВ, ровно и целиком, укладывающихся в проводнике полного витка В-1 рассматриваемого приёмного соленоида, является условием минимума напряжённости магнитного поля. Отсюда, дополним условие Формулы 2, что бы оно описывало максимум напряжённости электрического поля 
, для случая увеличения частоты переменного тока в соленоиде, когда длина λ эквивалентной ЭМВ, меньше длины l проводника полного витка соленоида, в нечётное количество раз:
λ = 
(при =) Формула 3
где:
– частота переменного тока проходящего, через соленоид;
– частота эквивалентной ЭМВ;
λ – длина эквивалентной ЭМВ;
l – длина проводника одного полного витка соленоида;
n – любое число, из множества натуральных чисел ;
Далее, дополним условие Формулы 2, что бы оно описывало минимум напряжённости электрического поля , для случая увеличения частоты переменного тока в соленоиде, когда длина λ эквивалентной ЭМВ, меньше длины l проводника полного витка соленоида, в чётное количество раз:
λ = 
(при =) Формула 4
где:
– частота переменного тока проходящего, через соленоид;
– частота эквивалентной ЭМВ;
λ – длина эквивалентной ЭМВ;
l – длина проводника одного полного витка соленоида;
n – любое число, из множества натуральных чисел ;
Теперь, построим условную схему напряжённости электрического поля , в проводнике одного полного витка В-1, рассматриваемого соленоида, для случая, когда длина λ эквивалентной ЭМВ, в 5 раз меньше длины l проводника полного витка В-1 рассматриваемого соленоида (см. Схему 9).
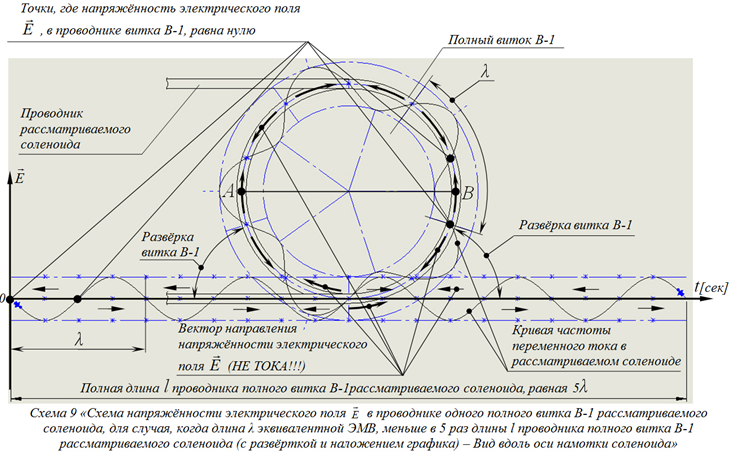
На этой схеме, путём осуществления развёртки полного витка В-1, покажем прямой участок l проводника, который, естественно, имеет ту же длину, что и проводник, составляющий полный виток В-1 рассматриваемого соленоида, и в который укладывается ровно 5λ эквивалентной ЭМВ. Наложим, на развёрнутый проводник, график частоты изменения напряжённости электрического поля в нём. На этом графике, так же, будет видно ровно пять периодов эквивалентной ЭМВ – то есть, 5λ эквивалентной ЭМВ. Далее, свернём этот график, с 5λ эквивалентной ЭМВ, в кольцо и наложим его на полный виток В-1 рассматриваемого соленоида. Теперь посмотрим, какие направления имеют вектора основной напряжённости электрического поля , в ранее рассмотренных любых двух, диаметрально противоположных, точках А и В. Как видно на Схеме 9, вектора основной напряжённости электрического поля , в точках А и В, имеют сонаправленное направление – то есть, направленное в одну сторону, и по касательной относительно кривой образованной витком В-1, и вдоль самого проводника витка В-1, в точности, как на Схеме 4, Схеме 5, Схеме 6 и Схеме 7, а это значит, что и вектора наведённой напряжённости электрического поля , так же, имеют сонаправленное направление, в том числе, и относительно векторов основной напряжённости электрического поля . Отсюда, очевидно, что условие содействия основной и наведённой напряжённостей электрического поля, описанное Формулой 2, так же соблюдено и в Формуле 3, что наглядно видно на Схеме 9, в рассмотренном выше примере-случае, когда длина λ эквивалентной ЭМВ, была в 5 раз меньше длины l проводника полного витка В-1 рассматриваемого соленоида, а равно, и для всех случаев вообще, когда длина λ эквивалентной ЭМВ, в нечётное число раз, меньше длины l проводника полного витка В-1 рассматриваемого соленоида, так же очевидно, что Формула 3 справедлива.
Следовательно, условием абсолютного максимума напряжённости СВЧ магнитного поля соленоида, можно назвать такой случай, когда, не нарушая условия Формулы 3, длина l, проводника полного витка В-1 рассматриваемого соленоида, минимальна, а число n максимально, что соответствует невероятно высоким частотам, при сверх малых габаритах соленоида, и что, в свою очередь, как уже отмечалось выше, открывает перспективу использования высоко эффективных, сверх мощных и сверх компактных электротехнических компонентов-источников магнитного поля при их весьма скромных габаритах и при их очень малых индуктивных характеристиках.
Любопытным, так же, является то, что у данного магнитного поля, в центре нет участков скомпенсированного (то есть, не подлежащего для прямого обнаружения, наблюдения и измерения) магнитного поля, какие наблюдаются у любого дипольного магнитного поля в районе полюсов.
Падение индуктивности в соленоиде, при переводе его в режим работы, согласно Формуле 3, когда он перестаёт быть индуктивной нагрузкой, переходя в состояние ёмкостной нагрузки, может обеспечить возможность специальной регулировки характеристик резонанса, в специальных колебательных контурах, когда необходимо повышение или понижение, индуктивных или ёмкостных характеристик соленоида.
Нужна помощь в продолжении исследований: email <leonovmgn74@gmail.com>; Skype «mgn74 74mgn»
[1] Соленоидами могут быть различные электротехнические элементы, как, например, катушки, обмотки и другие, в основе работы которых, лежит магнитное поле, магнитная индукция и индуктивность.
[2] Под осью полюсов здесь подразумевается воображаемая линия, перпендикулярная границе между северным «N» и южным «S» полюсами магнитного поля, в точке пересечения границы между северным «N» и южным «S» полюсами магнитного поля, а так же соединяющая северный «N» и южный «S» полюса магнитного поля, или воображаемая линия, совпадающая с осью намотки ИЭ.
[3] Плоскости, параллельные Оси полюсов и совпадающие с Осью полюсов.
[4] То есть, такой электромагнитной волны, частота которой полностью совпадает с частотой переменного тока, на котором работает рассматриваемый соленоид;
[5] То есть, когда, глядя на этот виток вдоль оси намотки, мы видим, что точка начала этого витка совпадает с точкой конца этого витка.
[6] Пара точек А и В, расположены на полном витке В-1 приёмного соленоида, диаметрально противоположно относительно Оси намотки витка В-1 приёмного соленоида и относительно друг друга таким образом, что бы через ось намотки витка В-1 приёмного соленоида и эти две воображаемые точки можно было провести воображаемую прямую.
Литература
- Ландау Л.Д., Лифшиц М.Е. ЭЛЕКТРОДИНАМИКА СПЛОШНЫХ СРЕД (Серия: «Теоретическая физика», том VIII). М., 1982.
- Трофимова Т.И. Курс физики: учеб. пособие для вузов. – М., 2006. – 560 с.
References
- Landau L.D., Lifshits M.E. ELECTRODINAMICA SPLOSHNIH SRED (Seriya: “Teoreticheskaya fizika”, tom VIII). M., 1982.
- Trofimova T. I. Kurs fiziki: ucheb. posobie – M., 2006. – 560 S.