РЕШЕНИЕ НЕЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ

Брыков Н.А.

Ассистент кафедры плазмогазодинамика и теплотехника, Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова, Санкт-Петербург

РЕШЕНИЕ НЕЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ

Аннотация

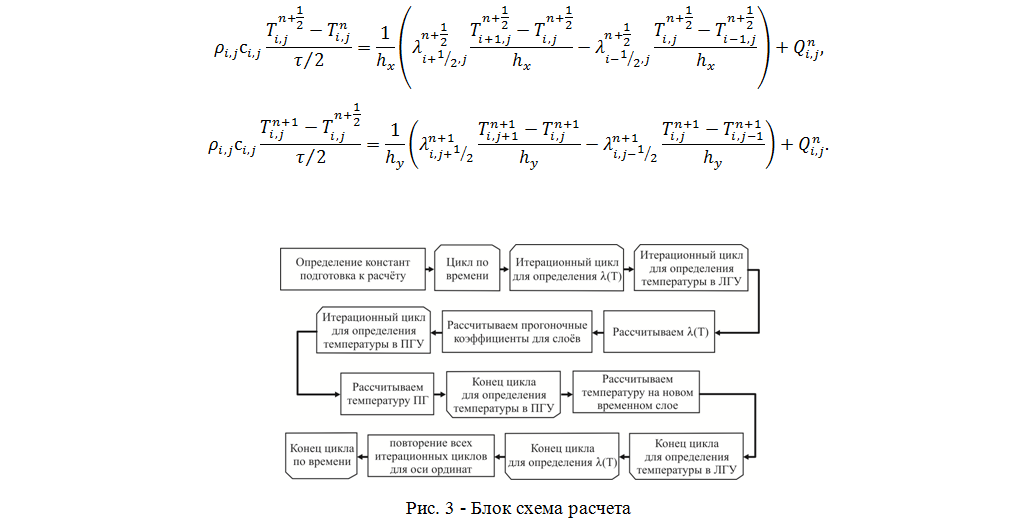
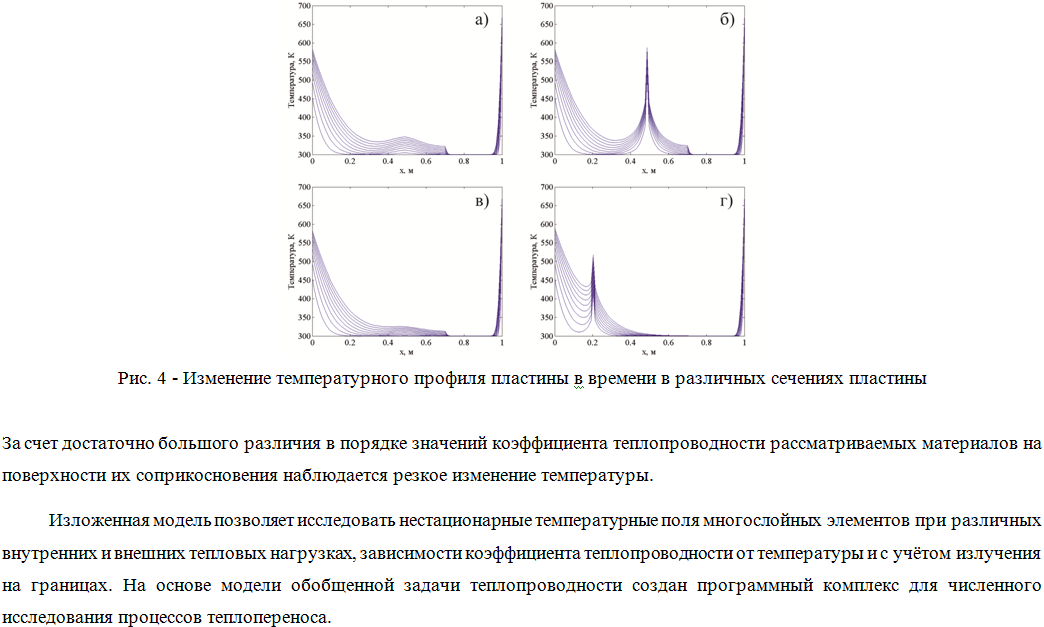
В статье рассмотрено численное решение нелинейной нестационарной задачи теплопроводности для определения температурного поля в многослойной пластине с внутренними источниками тепла. В модели учитывается зависимость коэффициента теплопроводности от температуры, и моделируется излучение на границах пластины. Изложена неявная двухслойная схема для метода прогонки. Дискретизация нестационарного уравнения теплопроводности производится с помощью локально одномерной, абсолютно устойчивой схемы. Представлены результаты расчета.

Ключевые слова: нестационарная теплопроводность, излучение на границе, метод прогонки.

Brykov N.A.

Assistant of the Department of heat engineering and plasmagasdynamic, Baltic State Technical University«VOENMEH» named after D.F. Ustinov, St. Petersburg

SOLUTION OF NONLINEAR TRANSIENT HEAT CONDUCTION PROBLEM

Abstract

The article deals with the numerical solution of nonlinear transient heat conduction problem for the determination of the temperature field in a multilayer plate with internal heat sources. The model takes into account the dependence of thermal conduction coefficient on the temperature, and is modeled on the radiation plate boundaries. Presented is an implicit two-layer scheme for the sweep method. Discretization of transient heat equation is performed by locally-dimensional, absolutely stable scheme.

Keywords: transient heat conduction, radiation on the borders, sweep method.

Литература

1. Чиркин В.С. Теплофизические свойства материалов ядерной техники. М.: Атомиздат, 1968 г. – 484 с.
2. Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие для вузов. – М.: Наука, 1989. – 432 с.

References

1. Chirkin V.S. Teplofizicheskie svojstva materialov jadernoj tehniki. M.: Atomizdat, 1968 g. – 484 s.
2. Samarskij A.A., Gulin A.V. Chislennye metody: Ucheb. posobie dlja vuzov. – M.: Nauka, 1989. – 432 s.