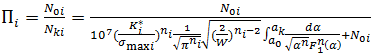ПОВРЕЖДЕННОСТЬ КАК ОСНОВНАЯ МЕРА УСТАЛОСТНОГО РАЗРУШЕНИЯ

Курбатов Ю. Е.¹, Кашеварова Г. Г.²

¹Аспирант; ²Доктор технических наук, профессор, Пермский национальный исследовательский политехнический университет

ПОВРЕЖДЕННОСТЬ КАК ОСНОВНАЯ МЕРА УСТАЛОСТНОГО РАЗРУШЕНИЯ 

Аннотация

Задача прогнозирования усталостной долговечности конструкций зданий является одной из наиболее актуальных и важных задач в строительстве. В данной работе рассмотрены различные модели накопления повреждений, с помощью которых можно определить величину поврежденности материала. Выполнен комплексный анализ данной усталостной характеристики, что позволяет обобщить разрозненные подходы к ее трактовке  и использовать ее при численном моделировании процесса усталостного разрушения.

Ключевые слова: поврежденность, усталостная долговечность, сплошность, кривая Вёлера.

Kurbatov Y. E.¹, Kashevarova G. G.²

¹ Postgraduate student; ² PhD in Engineering, Professor, Perm National Research Polytechnic University

DAMAGEABILITY AS A BASIC MEASURE OF THE FATIGUE FRACTURE

 Abstract

The problem of forecasting the durability of building structures is one of the most urgent and important tasks in construction. Different models of damage accumulation which help to quantify the amount of the material damageability are considered in this article. Performed a comprehensive analysis of this fatigue characteristic, which enables to generalize the disparate approaches to its definition and use it in the numerical modeling of fatigue fracture.

Keywords: damageability, fatigue life, continuity, Wohler curve.

Циклические нагрузки являются одними из основных факторов воздействия на бетонные и железобетонные конструкции промышленных и транспортных сооружений. В результате данные нагрузки могут вызывать усталостное разрушение отдельных узлов или целых конструкций.

Согласно [1, стр.3] усталостное разрушение – это разрушение материала нагружаемого объекта до полной потери его прочности или работоспособности вследствие распространения усталостной трещины. При этом основным параметром, характеризующим усталостную выносливость того или иного материала является циклическая долговечность - число циклов напряжений или деформаций, выдержанных нагруженным объектом до образования усталостной трещины определенной протяженности или до усталостного разрушения (в соответствии с тем же нормативным документом [1, стр.13]).

Однако помимо знания информации о количестве циклов до разрушения (которую чаще всего можно получить из лабораторных испытаний), необходимо также контролировать процесс накопления усталостных повреждений, фиксируя появление дефектов во времени. К сожалению, на сегодняшний день отсутствуют объективные количественные характеристики физического состояния материала, которые бы однозначно оценивали кинетику накопления усталостных повреждений и оставшийся ресурс конструкций. Процесс образования усталостной трещины сопровождается определенным изменением физических свойств материала, но при этом не может быть количественно интерпретирован прямыми физическими методами. В результате, на практике принято использовать формальную методологию оценки усталостного повреждения. В основе данной методологии лежит понятие поврежденности материала – это универсальная мера, позволяющая сопоставлять результаты испытаний, проводимых по разным программам, и переходить от результатов эксперимента к оценке усталостной долговечности в эксплуатации  [2, стр.52]. Существует несколько моделей поврежденности материала, основанные на различных подходах к определению данной величины.

Согласно простейшей модели поврежденности Пальмгрена-Майнера, мерой усталостного повреждения объекта служит отношение текущего числа циклов нагружения  к долговечности (числу циклов до разрушения)  при заданном уровне циклических напряжений σ:

    (1)

Зависимость N_k = f(σ) принимается по усталостным кривым (кривым Вёлера), которые характеризуют зависимость между максимальными напряжениями или амплитудами цикла и циклической долговечностью одинаковых образцов [1, стр.13].

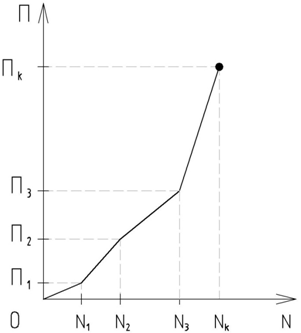
На практике оценка усталостного повреждения по формуле Пальмгрена-Майнера является наиболее распространенной в силу своей простоты. При этом принимается, что процесс накопления повреждений является линейным, т.е. ΔN  циклов в начале процесса нагружения создают точно такое же повреждение, как и ΔN циклов в середине или конце процесса нагружения образца (см. рис. 1). Таким образом, данный подход основывается на гипотезе линейного суммирования усталостных повреждений.

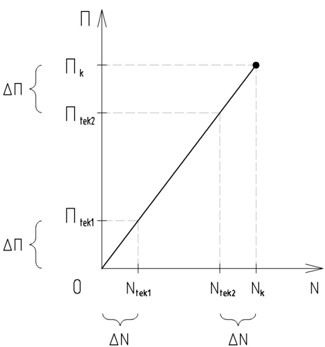
Рис. 1 – Гипотеза линейного суммирования усталостных повреждений

 

В рамках данной гипотезы существует два направления в трактовке величины П_k , соответствующей моменту разрушения: кинетический и феноменологический. Согласно первому П_k = 1 и разрушение происходит при прохождении критического числа циклов, обусловленного усталостной кривой. На практике П_k далеко не всегда равна единице, что можно объяснить неоднозначностью величины усталостной долговечности, которая напрямую зависит от принятого критерия разрушения при испытаниях и может варьироваться.

Согласно [3, стр.14], многочисленные экспериментальные проверки показали, что сумма накопленных повреждений к моменту разрушения может быть заключена в интервале от 0,2 до14. Данный факт используют при феноменологическом подходе - считая П_k ≠ 1, для разных материалов, типов конструкций, программ нагружения и их параметров пытаются определить конкретное значение данной величины.

В рамках кинетического подхода данная проблема решается путем учета дополнительных факторов, влияющих на результат, которые позволяют учесть или исключить взаимовлияние различных циклов (истории нагружения), сопровождающееся изменением деформационных свойств материала. Таким образом, выявляется нелинейный характер накопления повреждений, что и обуславливает возникновение ошибок расчета при использовании классической формулы (1), а также зависимость результата от очередности суммирования. Для устранения данных ошибок полный спектр циклов нагружения разбит на ряд групп, для каждой из которых действует свой закон накопления повреждений, но при этом все они остаются линейными:

   (2)

Рис. 2 – Гипотеза квазилинейного суммирования усталостных повреждений

 

Логичным развитием данной методики определения поврежденности материала является переход к гипотезе нелинейного суммирования усталостных повреждений, которая значительно сложнее описывает процесс накопления повреждений, но при этом позволяет приблизиться к фактическим показателям в реальных конструкциях. В работе [3] дается краткий обзор некоторых нелинейных моделей.

В модели рассеянной поврежденности Качанова-Работнова рассматриваемая величина поврежденности принимается равной:

ω = 1 - Ψ   (3)

где Ψ – сплошность материала, характеризующая степень распространения дефектов по объему нагружаемого тела.

Сплошность можно определить как отношение номинального напряжения в сечении к фактическому, которое в свою очередь становится больше за счет ослабления рабочего сечения различными пустотами и повреждениями. Очевидно, что абсолютно неповрежденному “идеальному” материалу соответствует Ψ = 1 и ω = 0, а для полностью разрушенного материала Ψ = 0; ω = 1.

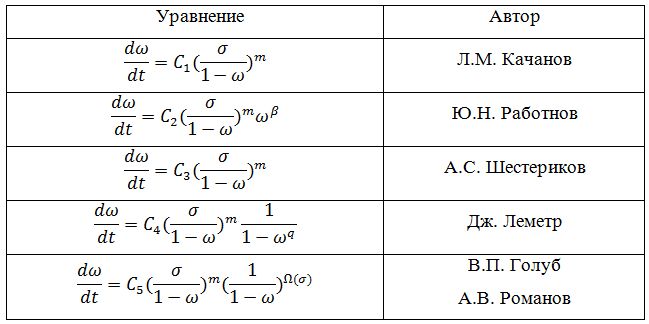
В таблице 1 приведены некоторые гипотезы накопления повреждений, постулирующие нелинейный характер роста поврежденности материала в рамках модели рассеянной поврежденности.

Таблица 1 – Модели накопления повреждений

 

В развитие данного подхода позднее были предложены модель тела с опасной точкой (рис.3, а), модель тела с опасным сечением Серенсена – Когаева (рис.3, б) и модель тела с опасной поверхностью Вагапова (рис.3, в) [4, 5]. В модели Серенсена – Когаева первичные усталостные повреждения  возникают не только в точке на поверхности, но и на некоторой глубине циклически деформируемого твердого тела. Модель Вагапова обнаруживает указанные повреждения не только в опасном сечении (с максимальным уровнем напряжения), но и на прилегающей к нему поверхности, где напряжения на 5…15 % меньше максимального.

В работе [3, стр.17] дается подробный анализ модели тела с опасным объемом, которая обобщает изложенные выше аспекты. При этом абсолютная мера поврежденности определяется как объем материала с критическим уровнем напряжений в нем (рис.3, г).

   

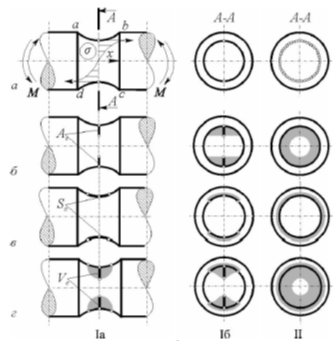
Рис. 3 – Схематическая иллюстрация моделей деформируемого твердого тела с опасной точкой (а), опасным сечением (б), опасной поверхностью (в) и опасным объемом (г) при статическом (Iа, Iб) и циклическом (II) нагружении

 

В модели тела с опасным объемом текущий уровень поврежденности материала описывается неравенством:

    (4)

где V_pγ  - объем материала с критическим уровнем напряжений; V₀ - рабочий объем элемента конструкции.

Согласно [3, стр.18], процедура расчета опасных объемов предполагает знание трехмерного напряженного состояния элементов, вызванного как локальным нагружением, так и объемным деформированием, а также определение критических (предельных) напряжений, которые служат критерием для ограничения соответствующих опасных областей. При этом различные опасные объемы могут дополнять и пересекаться друг с другом, формируя комплексное повреждение в материале и создавая разнообразные расчетные ситуации. Важно отметить, что рабочий объем V₀ представляет собой не весь объем деформируемого твердого тела, а лишь объем предельно допустимого износа. Это соотносится с тем фактом, что усталостное разрушение происходит в результате разделения объема образца трещиной на отдельные “куски”, объем которых остается целостным.

 

Таблица 2 – Классификация динамических опасных объемов

Авторы модели Сосновский Л. А., Журавков М. А. и Щербаков С. С. выделяют несколько типов опасных объемов, как статических, так и динамических (актуальных для циклического нагружения). Последние приведены в таблице 2.

Резюмируя данный подход, следует отметить, что в силу своего многообразия эффекты взаимодействия повреждений различных типов не могут быть точно описаны или спрогнозированы. Однако использование модели опасных объемов позволяет получить эквивалент комплекса повреждений, благодаря пропорциональности критического объема уровню напряжений (деформаций) а, следовательно, и количеству (концентрации) дефектов и повреждений.

Еще одна модель поврежденности была разработана в рамках линейной механики разрушения на основе идей, предложенных Гриффитсом. В соответствии с данной моделью свободная от дефектов среда содержит хотя бы одну остроконечную трещину, кинетика развития которой и определяет усталостную долговечность материала. При этом поврежденность определяется длиной усталостной трещины.

Согласно [6, стр.157], критический коэффициент интенсивности напряжений при обобщенном плоском напряженном состоянии  с одной стороны характеризует способность материала сопротивляться развитию трещины, а с другой входит в условия разрушения, устанавливающие ту величину коэффициента интенсивности напряжений, при котором наступает резкий неконтролируемый рост трещины.

Некоторыми исследователями на основе различных физических представлений были получены зависимости скорости роста трещины от числа циклов приложенного напряжения и длины трещины. Недостатком этих зависимостей является то, что они удовлетворительно описывают лишь какие-то определенные участки кривых роста усталостных трещин и не носят общего характера. С развитием механики разрушения стало возможным рассмотреть процесс роста усталостных трещин с более общих позиций. При этом было установлено, что скорость роста трещины зависит также и от коэффициента интенсивности напряжений (КИН). В работе [6, стр.160] приводятся основные уравнения, описывающие данную зависимость:

    (5) уравнение Пэриса     (6) уравнение Эрдогана     (7) уравнение Формана     (8) где К = К₁; ΔК = К_max - K_min

К_max, K_min – КИНы при максимальной и минимальной нагрузках цикла;

r – коэффициент ассиметрии цикла;

К* – наибольший коэффициент интенсивности напряжений цикла при скорости роста трещины  м/цикл;

K_C – критический коэффициент интенсивности напряжений при обобщенном плоском напряженном состоянии;

C,C₁,C₂,C₃,m,M,n – экспериментально определяемые константы.

Основная задача в данном случае состоит в том, чтобы охарактеризовать кинетику роста усталостной трещины, используя соответствующее уравнение, и оценить прогнозируемый срок службы.

Для вычисления поврежденности возьмем за основу уравнение (5) и примем  . В результате получим дифференциальное уравнение развития трещины:

    (9) где а – длина трещины;  N – число циклов. Преобразуем полученное уравнение и проинтегрируем его:     (10)     (11)

где a₀ – начальная длина трещины, соответствующая числу циклов N₀; a_k – критическая длина трещины, соответствующая числу циклов в момент разрушения N_k,

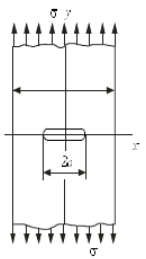
Для дальнейшего вычисления интеграла необходимо конкретизировать форму рассчитываемого элемента. В качестве примера рассмотрим полосу с центральной трещиной при одноосном растяжении (рис. 4).

Рис. 4 – Полоса с центральной трещиной

  Для данного конструктивного элемента:     (12) где   W – ширина полосы Подставив (12) в (11), получим:    (13)

Таким образом, можно получить остаточную долговечность элемента конструкции с трещиной. Как отмечается в [6, стр.162], основная доля циклов усталостной долговечности приходится на начальный период роста трещины. По мере развития трещины происходит увеличение скорости роста, поэтому на стадию быстрого роста приходится лишь небольшая часть срока службы.

Используя выражение (13), попробуем вычислить поврежденность элемента через формулу (2):

     (14)

С учетом того, что ,n_i, a_k зависят от σ_{max i}, получим нелинейную зависимость поврежденности материала от начальной длины трещины:

    (15)

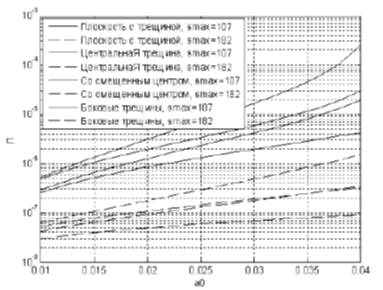
На рисунке 5 приведен график зависимости поврежденности от начальной длины трещины; на рисунке 6 - от числа приложенных циклов для рассматриваемого образца с различными видами трещин при наибольшем и наименьшем значении максимальной нагрузки.

Рис. 5 – Зависимость поврежденности за один цикл от начальной длины трещины при наибольшем и наименьшем значении максимальной нагрузки

 

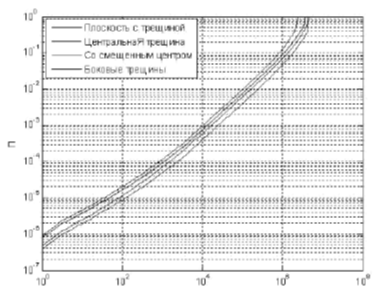
Рис. 6 – Зависимость поврежденности от числа циклов нагружения

 

Таким образом, можно сделать вывод о нелинейном характере  процесса накопления усталостных повреждений (с изменяющейся скоростью развития трещины). Для анализа остаточной долговечности необходимо учитывать зависимость поврежденности за цикл от текущей длины трещины и уровня действующего максимального напряжения в цикле.

В работе [7] развивается модель изотропной вязкой континуальной поврежденности и проведена экспериментальная проверка базовых определяющих соотношений и прогнозируемых, на основе применения модели, результатов. Здесь рассматривается процесс зарождения и роста усталостной трещины в нелинейно упругом материале АД37, который находится под действием циклической нагрузки. Математическая модель разрушения включает в себя непосредственный расчет процесса зарождения и развития дисперсных дефектов и макроскопической трещины. При этом поврежденность материала учитывается с помощью эквивалентных параметров нелинейной упругости.

Будем считать, что повреждения, накопленные в материале вблизи вершины трещины, могут быть описаны с помощью скалярной функции времени D (t) . При этом в процессе нагрузки величина D принимает значение [0,1] на отрезке времени t. Тогда D = 0 отвечает случаю, когда повреждения отсутствуют, значение D = 1 соответствует уровню повреждений, при котором материал полностью разрушился в рассмотренной точке.

Классическое определяющее уравнение механики континуальной квазихрупкой поврежденности [8] имеет вид:

     (16)

где σ_ij  - тензор напряжений Коши; ε_ab – тензор линейной деформации; D – поврежденность материала;  λ_ijab – тензор линейной упругости.

В свою очередь тензор линейной деформации можно найти по следующей формуле:

    (17)

где u(x) – вектор перемещений.

Соотношение (16) дает возможность учесть влияние меры поврежденности D на упругие свойства материала в качестве фактора, который уменьшает его жесткость.

Используя в качестве условия эквивалентности упругих свойств модели нелинейной механики случайно неоднородных сред [8,9,10] и механики континуальной поврежденности, авторы [7] устанавливают взаимно однозначное соответствие между параметром ξ, который выражает количество микротрещин в единице объема и скалярной мерой поврежденности D (см. формулу 18).

    (18)

Отсюда можно выразить величину поврежденности:     (19)

где a_μ – длина микротрещины.

На рисунке 7 приведены зависимости эквивалентных модуля Юнга и модуля объемного сжатия от меры поврежденности , полученные для рассматриваемого материала в случае плоского сдвига.

 

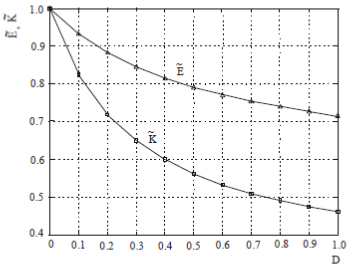
Рис. 7 – Развитие поврежденности в материале

 

Установленное в [7, стр.125] соответствие между скалярным параметром меры поврежденности D (который может определяться из эксперимента на одномерное растяжение) и аналитическим дисперсным параметром ξ, который характеризует число дискообразных микротрещин в единице объема, дает возможность исследования в трехмерной постановке на базе классических уравнений механики сплошной среды влияния вязкой поврежденности на процесс распространения усталостной трещины.

Таким образом, существует несколько моделей поврежденности, использующие различные подходы и разделы механики для определения усталостной долговечности того или иного материала. В силу малой изученности процессов усталостного накопления повреждений в бетоне, рассмотренные в данной статье модели могут быть использованы при численном анализе процессов его усталостного разрушения. При этом должны учитываться отличительные особенности структурного состава бетона, как композита, в сравнении с металлами, для которых изначально разрабатывались изложенные выше методики.

Литература

1. ГОСТ 23207-78. Сопротивление усталости. Основные термины, определения и обозначения. – Введ. 1979-01-01. – Москва: Издательство стандартов, 1978. – 49с.
2. Сопротивление усталости элементов конструкций: учебник / А.З. Воробьев [и др.]. – М.: Машиностроение, 1990. – 240с.
3. Сосновский Л. Концепции поврежденности материалов / Л. Сосновский, С. Щербаков // Вестник ТНТУ. – 2011. – Спецвыпуск – часть 1. – С.14-23.
4. Серенсен, С.В. Несущая способность и расчеты деталей машин на прочность [Текст] / С.В. Серенсен, В.П. Когаев, Р.М. Шнейдерович. – М. – 488 с.
5. Вагапов, Р.Д. Статистическая теория рассеивания случайной координаты повреждения тела [Текст] / Р.Д. Вагапов // Машиноведение. –1970. – № 4. – С. 63–74.
6. Кулик Н.С. Сравнительный анализ поврежденности и остаточной долговечности элементов конструкции с различными дефектами типа трещин при действии спектра нагрузок / Н.С. Кулик, А.Г. Кучер, В.Е. Мильцов // Авиационно-космическая техника и технология. – 2009. – № 10 (67). – С.156-166.
7. Климюк А.Н. Идентификация определяющих параметров модели усталостного разрушения пластины / А.Н. Климюк, И.В. Лиманский // Авиационно-космическая техника и технология. – 2008. – № 1. – С.123-133.
8. Болотин В.В. Ресурс машин и конструкций: Учебник / В.В. Болотин. – М.: Машиностроение,1990. – 448с.
9. Гусев Б.В., Кондращенко В.И., Маслов Б.П., Файвусович Ф.С. Формирование структуры композиционных материалов и их свойства. – М.: Научный Мир, 2006. – 560с.
10. Хорошун Л.П., Маслов Б.П. Нелинейные свойства композитных материалов стохастической структуры. – К.: Наук. думка, 1993. – 132 с.

References

1. GOST 23207-78. Soprotivlenie ustalosti. Osnovnye terminy, opredelenija i oboznachenija. – Vved. 1979-01-01. – Moskva: Izdatelstvo standartov, 1978. – 49s.
2. Soprotivlenie ustalosti elementov konstrukcij: uchebnik / A.Z. Vorobiev [i dr.]. – M.: Mashinostroenie, 1990. – 240s.
3. Sosnovskij L. Koncepcii povrezhdennosti materialov / L. Sosnovskij, S. Shherbakov // Vіsnik TNTU. – 2011. – Specvipusk – chastina 1. – S.14-23.
4. Serensen S.V. Nesushhaja sposobnost i raschety detalej mashin na prochnost [Tekst] / S.V. Serensen, V.P. Kogaev, R.M. Shnejderovich. – M. – 488 s.
5. Vagapov R.D. Statisticheskaja teorija rasseivanija sluchajnoj koordinaty povrezhdenija tela [Tekst] / R.D. Vagapov // Mashinovedenie. –1970. – № 4. – S. 63–74.
6. Kulik N.S. Sravnitelnyj analiz povrezhdennosti i ostatochnoj dolgovechnosti elementov konstrukcii s razlichnymi defektami tipa treshhin pri dejstvii spektra nagruzok / N.S. Kulik, A.G. Kucher, V.E. Milcov // Aviacionno-kosmicheskaja tehnika i tehnologija. – 2009. – № 10 (67). – S.156-166.
7. Klimjuk A.N. Identifikacija opredeljajushih parametrov modeli ustalostnogo razrushenija plastiny / A.N. Klimjuk, I.V. Limanskij // Aviacionno-kosmicheskaja tehnika i tehnologija. – 2008. – № 1. – S.123-133.
8. Bolotin V.V. Resurs mashin i konstrukcij: Uchebnik / V.V. Bolotin. – M.: Mashinostroenie,1990. – 448s.
9. Gusev B.V., Kondrashhenko V.I., Maslov B.P., Fajvusovich F.S. Formirovanie struktury kompozicionnyh materialov i ih svojstva. – M.: Nauchnyj Mir, 2006. – 560s.
10. Horoshun L.P., Maslov B.P. Nelinejnye svojstva kompozitnyh materialov stohasticheskoj struktury. – K.: Nauk. dumka, 1993. – 132 s.