МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДЛЯ КЛАСТЕРИЗАЦИИ ДАННЫХ НА ОСНОВЕ ОБУЧАЮЩЕЙ ВЫБОРКИ

Кротов Л.Н.¹, Кротова Е.Л.², Рукшин С.А.³

¹Доктор физико-математических наук, профессор, кафедра Прикладной физики,  кандидат физико-математических наук, доцент, кафедра Высшей математики, ³аспирант, кафедра Прикладной физики, Пермский национальный исследовательский политехнический университет

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДЛЯ КЛАСТЕРИЗАЦИИ ДАННЫХ НА ОСНОВЕ ОБУЧАЮЩЕЙ ВЫБОРКИ

Аннотация

Решается задача по разбиению наблюдений на основе анализа метрик качества предоставляемой провайдером услуги на 2 класса на основе метода k-means. Основная задача – выявить класс элементов, максимально соответствующий обучающей выборке. Впоследствии планируется увеличивать количество параметров, по которым проводится разбиение наблюдений на классы. Так же возможно увеличение градации схожести полученных классов с обучающей выборкой для выявления всех или максимального количества элементов совпадающих с обучающей выборкой.

Ключевые слова: математическое моделирование, статистическая кластеризация, статистический критерий.

Krotov L.N.¹, Krotova E.L.², Rukshin S.A.³

¹PhD in Physics and Mathematics, professor, ² PhD in Physics and Mathematics, Associate professor, ³ postgraduate student, Perm national research polytechnic university

MATHEMATICAL SIMULATION FOR THE CLUSTERING OF DATA ON THE BASIS OF LEARNING SELECTION

Abstract

The problem on partition of observations on the basis of the analysis of metrics of quality of the service delivered by provider on 2 classes on the basis of the k-means method is solved. The main objective is to reveal the class of elements which is the most corresponding to learning selection. Afterwards it is planned to increase the number of parameters in which partition of observations on classes is carried out. Increase in gradation of similarity of the received classes with learning selection for detection of all or the maximum quantity of the elements matching learning selection is also possible.

Keywords: mathematical simulation, statistical clustering, statistical criterion.

 

Актуальность исследования заключается в том, что решение задачи кластеризации может быть использовано для устранения внутренних проблем на производстве и вычленения слабых звеньев производственного процесса. Так же методы кластерного анализа могут применяться в других отраслях (распознавание образов без учителя, стратификация, таксономия, автоматическая классификация и т.п.) [1].

Метод k-means (метод k-средних) – наиболее популярный метод кластеризации (именно поэтому он был выбран для решения поставленной задачи). Суть метода сводится к тому, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров. При этом он разбивает множество элементов векторного пространства на заранее известное число кластеров k. Основная идея заключается в том, что на каждой итерации пересчитывается центр масс для каждого кластера, полученного на предыдущем шаге, затем векторы разбиваются на кластеры вновь в соответствии с тем, какой из новых центров оказался ближе по выбранной метрике. Алгоритм завершается, когда на какой-то итерации не происходит изменения центра масс кластеров. Это происходит за конечное число итераций, так как количество возможных разбиений конечного множества конечно, а на каждом шаге суммарное квадратичное отклонение не увеличивается, поэтому зацикливание невозможно [2].

Цель работы состоит в том, чтобы из общего множества наблюдений вычленить класс наиболее близкий к обучающей выборке. Для решения данной задачи был использован следующий подход:

- С сервера взята выборка данных, включающая в себя данные по 17528 наблюдениям, по каждому из которых зафиксированы 14 метрик.

- Определены ранги параметров, которые влияют на качество услуги а именно 2 главных параметра, имеющих наибольшую корреляцию с обучающей выборкой: среднее время установления соединения и среднее количество пакетов данных = р1, переданных без повторной передачи = р2.

По этим двум главным параметрам и проводим разбиение методом к-средних первоначально на два максимально противоположных класса.

Для этого строим матрицу вышеупомянутой выборки– в ней получается 17528 строк (количество наблюдений) и 14 столбцов (количество метрик), соответствующих метрик, после чего формируем матрицу состоящую все из тех же 17528 строк, но двух столбцов для получения матрицы параметров. При этом в полученной после деления матрицы первый соответствует параметру р1 – с наивысшим рангом, а второй соответствует параметру р2 со вторым рангом [3,4].

В результате получаем матрицу параметров Х = [p1; p2], которая имеет 17528 строк по количеству наблюдений, и 2 столбца со значениями вычисленных параметров. Представление этой матрицы графически является координатной плоскостью, где каждый i-ый абонент будет представлен в виде точки с координатами p1(i); p2(i), значения p1 и p2 откладываются вдоль осей р1 по горизонтали, р2  - по вертикали, таким образом получаем распределение абонентов, характеризуемых параметрами р1 и р2. При этом не нужно путать с графиком функции в координатах, здесь горизонтальная и вертикальная оси – никак не связаны между собой и значение по вертикали не зависит от горизонтальных значений, величины – независимы.

Далее используем функцию, которая встроена в Matlab и которая позволяет разбить объекты в множестве таким образом, чтобы объекты разных классов как можно больше отличались друг от друга, а наблюдения внутри класса были максимально схожими между собой.  Функция kmeans.

[IDX, C, sumd, D] = kmeans(X, 2,  'distance', 'cityblock', 'start', 'sample');

Здесь ее характеризуют следующие параметры, они указаны  в скобках после самой функции:

- сама случайная величина, в данном случае наша матрица Х = [p1; p2];

- ее размерность 2 в нашем случае, поскольку мы классифицируем объекты по двум параметрам р1 и р2;

- ‘distance’ это мера расстояний между объектами, которая используется для нахождения внутригрупповых средних расстояний;

- ‘start’ – это координаты задания центроидов;

Для нашего исследования были выбраны Манхэттенское расстояние – ‘cityblock’ и метод задания начальных координат центроидов классов ‘sample’ поскольку при них была получена наиболее адекватная визуальная картина разбиения на классы.

Применив данную функцию, в Matlab автоматически рассчитывается разбиение элементов нашей матрицы Х = [p1; p2] на два класса.

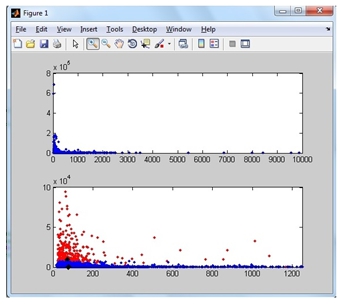
После этого мы делаем 2 выборки наблюдений из полученных при разбиении классов: то есть выбираем все элементы в первом классе и выбираем отдельно все элементы во втором классе.   В нашем исследовании выборка у нас состоит из 17528 в обоих классах, при разбиении функцией kmeans получилось 2 класса, включающих в себя 373 и 17155 элементов.  Результаты разбиения на классы можно увидеть на рисунке ниже.

Рис.1 Результат разбиения элементов на классы с применением k-means в пакете MatLab.

Проведя процедуру сравнения элементов каждого из классов по отдельности файлом обучающей выборки находим совпадения элементов и делим результат количества совпадений на общее количество элементов в данном классе и получаем результат отношения элементов в классе к общему числу элементов в этом классе. Далее для получения процентного соотношения можно результат отношения умножить на 100%.

Таким образом, у нас получилось в классе из 373 элементов, 363 совпали с обучающей выборкой,   что дает результат 363/373=0,9732*100%=97,32%.

Во втором классе аналогично из 17155 элементов, 2636 совпали с обучающей выборкой, что дает результат 2636/17155=0,1537*100%=15,37%.

Теперь становится понятно, что в классе из 373 элементов находятся 363 по которым произошло совпадение с обучающей выборкой концентрацией совпавших элементов более 97%! А класс , содержащий 17155 элементов содержит в себе всего чуть более 15% совпадений с обучающей выборкой, включает в себя около 85% элементов, не совпавших с обучающей выборкой. Однако, стоит заметить, что хоть в процентном соотношении в классе  с 17155 элементами 15% совпадений, но в абсолютном количестве 2636 – это много, следовательно,  предлагаем класс с 373 элементами оставить таким, какой он получился, а класс в 17155 элементами разбить дальше еще на 2 класса, затем (при потребности) еще один из вновь полученных классов разбить еще на 2 класса, повторить эту процедуру оптимальное число раз. При этом, при каждом разделении на 2 класса у нас будут выявляться вновь классы с большим или меньшим числом совпадений элементов с обучающей выборкой. В итоге взяв объединение всех классов с высокой концентрацией совпадений мы вычленим элементы, совпадающие с обучающей выборкой из всего массива наблюдений.

Таким образом, предложенная методика кластеризации показала удовлетворительные результаты и ее продолжение при постоянном сравнении с новыми данными обучающих выборок позволит решить поставленную задачу. В дальнейшем полученные результаты можно использовать так же при исследовании влияния параметров трафика на качество обслуживания [5].

Литература

1. Мандель И.Д. — М.: Финансы и статистика, 1988. — 176 c.
2. https://ru.wikipedia.org/wiki/K-means.
3. M. Mirkes, K-means and K-medoids applet. University of Leicester, 2011.
4. Е. Л. Бородулина, Е. Л. Кротова, “Метод расщепления строго устойчивых смесей нормального закона для показателей устойчивости α=1α=1 и α=2α=2”, Матем. моделирование, 20:7 (2008), 3–12.
5. Меркулова Ирина Александровна. Исследование и разработка методов анализа трафика Интернет-провайдера: дис. ... канд. техн. наук : 05.12.13 Самара, 2007 144 с. РГБ ОД, 61:07-5/2070.

References

1. Mandel' I.D. — M.: Finansy i statistika, 1988. — 176 c.
2. https://ru.wikipedia.org/wiki/K-means.
3. M. Mirkes, K-means and K-medoids applet. University of Leicester, 2011.
4. L. Borodulina, E. L. Krotova, “Metod rasshheplenija strogo ustojchivyh smesej normal'nogo zakona dlja pokazatelej ustojchivosti α=1α=1 i α=2α=2”, Matem. modelirovanie, 20:7 (2008), 3–12.
5. Merkulova Irina Aleksandrovna. Issledovanie i razrabotka metodov analiza trafika Internet-provajdera: dis. ... kand. tehn. nauk : 05.12.13 Samara, 2007 144 s. RGB OD, 61:07-5/2070.