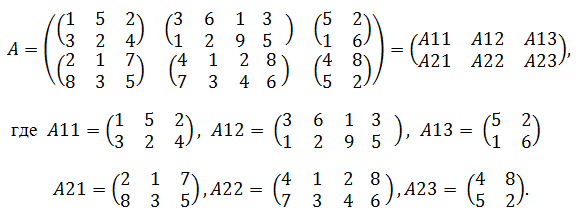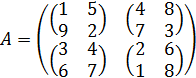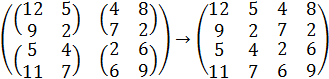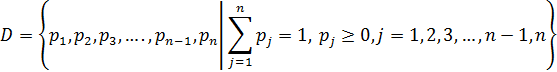ИГРЫ С КЛЕТОЧНЫМИ МАТРИЦАМИ
Яксубаев К.Д.
Кандидат физико-математических наук, Астраханский государственный архитектурно-строительный университет
ИГРЫ С КЛЕТОЧНЫМИ МАТРИЦАМИ
Аннотация
В статье рассматриваются игры с клеточными матрицами. Показано, что в соответствии с идеологией академика Л.С. Понтрягина примененной им в теории дифференциальных игр матричные игры с разным порядком ходов нужно считать различными играми.
В работе игра в чистых стратегиях с клеточной матрицей сведена к игре на графе. Причем играм с различным порядком ходов, но с одной и той же матрицей, будут соответствовать разные графы и разный порядок развертывания клеточной матрицы в граф.
Показано, что теорема Неймана о существовании седловой точки для
смешанной игры с клеточной матрицей с произвольной глубиной вложения матриц-клеток тоже верна.
Ключевые слова: клеточные матрицы, теория игр, цена игры.
Yaksubaev K.D.
PhD in Physics and Mathematics, Russian State Astrakhan University of Architecture and Building
GAME WITH CELLULAR MATRICES
Abstract
The article discusses the game with the cell matrices shows that in accordance with the ideology of academician L.S. Pontryagin applied in the theory of differential games matrix games with different order of moves should be considered different games.
In the game in pure strategies with the cell matrix is reduced to a game on a graph. Moreover, the games with different order of moves, but with the same matrix, will correspond to different columns and different order of deployment of the cellular matrix into a graph.
It is shown that the Neumann theorem on the existence of saddle points for game mixed with cellular matrix with an arbitrary nesting depth of matrix cells is also true.
Keywords: cell matrix, game theory, price of the game.
Матричные игры обобщались в разных направлениях [1]. Одно из возможных обобщений матричных игр это игры с клеточными матрицами.
Клеточными матрицами называются матрицы вида:
Матрица ![]() , называется фактор-матрицей. Она
, называется фактор-матрицей. Она
состоит из имен матриц-клеток.
Описание игры в чистых стратегиях.
Игроки. Играют два игрока: P и Q. Игрок P это первый игрок, а Q это второй игрок.
Платежная матрица. Платежная матрица является матрицей выигрыша первого игрока, и одновременно матрицей проигрыша второго игрока.
Цель игры. Первый игрок стремится максимизировать выигрыш, а второй игрок стремится минимизировать проигрыш.
Стратегии. Игрок P выбирает строки, а игрок Q выбирает столбцы.
Ход игры. Игра длится два хода.
Первый ход: игра сначала ведется на фактор-матрице. В результате игры будет выбрана конкретная матрица-клетка.
Второй ход. Игра продолжается на выбранной матрице-клетке. Выбор столбца или строки называется полуходом.
Порядок ходов и тип игры.
Тип игры обозначается TG=1212, или TG1212. В игре этого типа игрок P ходит дважды первым, а игрок Q дважды вторым. Всего возможны четыре варианта игры.
| Тип игры | Игрок P | Игрок Q | Цена игры |
| TG1212 | Первый, первый | Второй, второй | V1212 |
| TG1221 | Первый, второй | Второй, первый | V1221 |
| TG2112 | Второй, первый | Первый, второй | V2112 |
| TG2121 | Второй, второй | Первый, первый | V2121 |
Решение игры типа TG1212 в чистых стратегиях.
Сначала игра ведется на каждой клетке-матрице отдельно. В результате шести отдельных игр получаем новую платежную матрицу:
На втором ходе получаем искомую цену игры: V1212= 3. Можно видеть, что выполняются неравенства: V1212≤ V1221, V2112 ≤ V2121. Для клеточной матрицы с глубиной вложения матриц-клеток равной n, мы будем иметь 2n различных игр.
Решение игры с клеточной матрицей в чистых стратегиях с помощью графов
Приведем решение игры с клеточной матрицей:
Тип игры: TG1212. Игра ведется в два хода. Оба раза первый игрок ходит первым, а второй игрок ходит вторым.
Принципы изображения графов.
При построении графа нужно соблюдать три правила: правило цветов, правило толщины ребер, правило кружочков.
Правило цветов. Ребра первого игрока изображаются всегда черным цветов. А ребра второго игрока розовым цветом.
Правило толщины ребер. Ребра первого игрока толще, чем ребра второго игрока.
Правило кружочков. Все кружочки, располагающиеся на одной горизонтали, должны быть идентичными.
Принципы развертывания клеточной матрицы в граф.
Развертывание клеточной матрицы происходит в два хода. На первом ходе развертывается фактор-матрица по строкам. На втором ходе развертываются все матрицы-клетки и тоже построчно.
Решение игры в чистых стратегиях. Для решения игры нужно следовать следующему принципу заполнения пустых кружочков графа.
Пустые кружочки графа заполняются при движении снизу вверх. При заполнении пустых кружочков применяется два оператора MAX, MIN. На ребрах нужно указывать операции MAX, MIN. Тогда число в вершине графа и будет искомой ценой игры.
Принципы изображения оптимальных полуходов игроков.
Оптимальные полуходы игроков изображаются двойными ребрами.
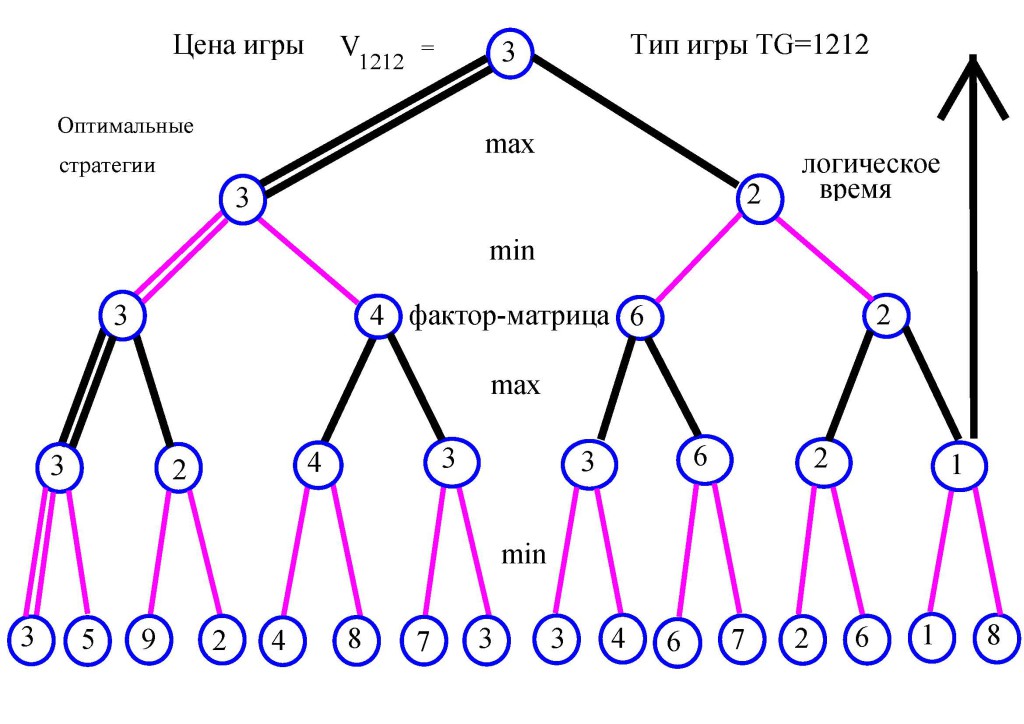
Логический граф игры с типом TG=1212 таков:
Решение клеточной игры в смешанных стратегиях
Игра с клеточной матрицей в смешанных стратегиях при глубине вложения матриц-клеток равной двум это игра с двойным розыгрышем. Сначала разыгрываются сами строки и столбцы фактор - матрицы. В результате этого розыгрыша выпадает, какая то матрица-клетка клеточной матрицы. Затем на выпавшей матрице-клетке разыгрываются строки и столбцы. Таким образом, мы видим, что игра с клеточными матрицами в смешанных стратегиях рассчитывается по формуле полной вероятности.
В этой игре определяются два типа вероятностей. Первый тип вероятностей это вероятности выбора и строк и столбцов для фактор - матрицы. Второй тип вероятностей это условные вероятности выбора строк и столбцов для каждой матрицы-клетки клеточной матрицы.
Порядок решения матричной игры в смешанных стратегиях для клеточных матриц таков. Сначала смешанная игра ведется на каждой матрице-клетке отдельно. Этим мы определяем цену смешанной игры на каждой такой матрице-клетке. А так же определяем вероятности выбора строк и столбцов на каждой матрице-клетке.
Затем подставляя цены смешанных игр в фактор - матрицу, мы получаем фактор - матрицу в численной форме. На этой фактор - матрице снова разыгрывается смешанная игра. Решая ее, мы получаем окончательное значение цены игры для исходной клеточной игры. И одновременно получаем вероятности выбора строк и столбцов фактор - матрицы. В итоге получаем теорему.
Теорема. Смешанная игра с клеточной матрицей всегда имеет седловую точку.
Таким образом, теорема Неймана о совпадении нижней и верхней цены игр, то есть о совпадении минимакса и максимина для смешанной игры с клеточными матрицами тоже верна.
Безусловно, теорема верна и для клеточных матриц с произвольной глубиной вложения матриц-клеток. Мы приводим теорему на клеточных матрицах с глубиной вложения равной двум, ради простоты изложения материала.
Если мы у матриц-клеток уберем матричные скобки, то получим одну большую матрицу:
В общем случае цены игр со смешанными стратегиями у этих двух матриц не совпадут, то есть игры в смешанных стратегиях для клеточных матриц есть имеют содержательный смысл.
Решение матричной игры в смешанных стратегиях методом Монте-Карло
При статистическом моделировании матричных игр со смешанными стратегиями нужно бросать случайные равномерно распределенные точки в область, задаваемую следующей системой неравенств и уравнений:
Это симплекс размерности n-1, расположенный в n-мерном пространстве. Сгенерировать случайные равномерно распределенные точки на множестве D можно следующим способом. Сначала генерируются n-1 случайных равномерно распределенных на отрезке векторов: ![]() длиной N. Потом проверяется условие:
длиной N. Потом проверяется условие:
Те индексы, которые не удовлетворяют этому условию, отбрасываются. После этого вектора снова перенумеровываются. Таким образом, мы получим, какое то количество случайных точек равномерно распределенных на симплексе размерности n-2. Затем по формуле
мы точки с симплекса размерности n-2 поднимаем на симплекс размерности n-1. Полученная последовательность точек будет случайной равномерно распределенной на симплексе D.
Вычислив значение целевой функции на сгенерированных случайных точках, мы получим новую платежную матрицу большого размера. Тем самым мы свели игру в смешанных стратегиях с маленькой исходной матрицей к матричной игре с седловой точкой в чистых стратегиях, но с матрицей большой размерности. Определив цену игры, и оптимальные строки и столбцы этой матрицы, мы тем самым найдем цену исходной игры в смешанных стратегиях, а также найдем и искомые вероятности.
Литература
- Н.Н. Воробьев. Основы теории игр. – М., 1984. S. - 495 s.
References
- N. Vorob'ev. Osnovy teorii igr. – M., 1984. S. - 495 s.