Наши журналы
Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

ЭФФЕКТЫ ВЫРЕЗАНИЯ ОБЪЕМА ИОНА И ПРОНИКНОВЕНИЯ ЗАРЯДА ИОНА В РАСТВОРИТЕЛЬ В НЕЛОКАЛЬНО-ЭЛЕКТРОСТАТИЧЕСКОЙ ТЕОРИИ СОЛЬВАТАЦИИ ДЛЯ ПОЛЮСНЫХ МОДЕЛЕЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ РАСТВОРИТЕЛЯ

Научная статья
Рубашкин А.А.
Конев Д. В.
Воротынцев М. А.
DOI:
https://doi.org/10.18454/IRJ.2016.47.106
Выпуск: № 5 (47), 2016
Опубликована:
2016/05/20
PDF

Рубашкин А.А.1, Конев Д. В.2, Воротынцев М. А.3

1Кандидат химических наук, Институт цитологии РАН, Санкт-Петербург, 2Кандидат химических наук, Институт проблем химической физики РАН, Черноголовка, 3Доктор физико-математических наук, МГУ им. М.В. Ломоносова, Москва

ЭФФЕКТЫ ВЫРЕЗАНИЯ ОБЪЕМА ИОНА И ПРОНИКНОВЕНИЯ ЗАРЯДА ИОНА В РАСТВОРИТЕЛЬ В НЕЛОКАЛЬНО-ЭЛЕКТРОСТАТИЧЕСКОЙ ТЕОРИИ СОЛЬВАТАЦИИ ДЛЯ ПОЛЮСНЫХ МОДЕЛЕЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ РАСТВОРИТЕЛЯ

Аннотация

В статье рассмотрено развитие нелокально-электростатической теории сольватации ионов на случай, когда учитывается эффект вырезания растворителя из объема, занятого ионом. Рассчитанная энергия сольватации иона в этой модели сравнивается с расчетом по теории (J. Chem. Phys., 1996), в которой не учитывается этот эффект, но используется модель размытой борновской сферы. Показано, что наша теория согласуется с экспериментом при малой величине доли заряда иона, находящегося в растворителе.

Ключевые слова: энергия сольватации, диэлектрическая функция растворителя, нелокальная электростатика

Rubashkin A.A.1, Konev D. V.2, Vorotyntsev M. A.3

1PhD in Chemistry, Institute of Cytology, Russian Academy of Sciences, Saint-Petersburg, Russia, 2PhD in Chemistry, Institute of Problems of Chemical Physics, Russian Academy of Sciences, Chernogolovka, Moscow region, Russia, 3PhD in Physics and Mathematics, Lomonosov Moscow State University, Moscow, Russia

EFFECTS OF CUT-OUT ION VOLUME AND OF PENITRATION OF THE ION CHARGE TO THE SOLVENT IN THE NONLOCAL ELECTROSTATICS SOLVATION THEORY FOR THE POLE MODELS OF DIELECTRIC FUNCTION OF THE SOLVENT

Abstract

The article considers the development of nonlocal electrostatic theory of ion solvation in the case when taken into account the effect of cut-out the ion volume from solvent. The calculated energy of ion solvation in this model is compared with the calculation on theory (J. Chem. Phys., 1996), which does not take into account this effect, but the model of smeared Born sphere is used. It is shown that our theory agrees with experiment at a small fraction of the ion charge in the solvent.

Keywords: solvation energy, dielectric function of solvent, nonlocal electrostatics.

В работе Корнышева и Сутманна [1] рассчитывались энергии сольватации W серии катионов щелочных металлов на основе нелокально-электростатической теории Догонадзе и Корнышева [2], не учитывающей вырезание из полярной среды полости, в которой находится ион (“эффект вырезания”). При этом в [1] была предложена модель "размытой борновской сферы" (SBS модель), в которой заряд иона распределен вдоль радиальной координаты. В [1] были представлены расчеты W для различных моделей диэлектрической функции растворителя ε(k), в том числе, учитывающих эффект переэкранирования диэлектрической функции.

В [1] было показано, что расчет энергии сольватации W для SBS модели понижает величину W по сравнению с расчетом, в котором весь заряд иона находится на борновской сфере. Однако в [1] не было представлено объяснение этого понижения расчетной энергии. Этот эффект анализировался нами в [3], где было показано, что часть заряда иона в SBS модели проникает в растворитель. Главный вывод [3] заключался в том, что понижение расчетной величины W обусловлено именно этой долей заряда иона, находящейся за пределами борновской сферы. В работе [3], как и в статье [1], считалось, что растворитель занимает все пространство, включая и внутреннюю область иона. Эффект вырезания объема иона из растворителя изучалcя в ряде работ [4-6].

В настоящей работе проведено изучение комбинации эффекта вырезания растворителя из объема, занятого ионом, с эффектом проникновения части заряда иона в растворитель. При этом использовались однополюсная и двухполюсная модели диэлектрической функции растворителя [7-9], а эффект переэкранирования диэлектрической функции (ЭП) не рассматривался. Отметим, что расчет энергии сольватации при одновременном учете ЭП с эффектами вырезания и проникновения части заряда в растворитель представляет значительно более сложную задачу, для решения которой нужно отдельное исследование.

Расчет энергии сольватации по формуле Догонадзе-Корнышева. Электростатическая составляющая энергии сольватации иона W радиуса ri согласно теории Догонадзе-Корнышева [2] рассчитывается по формуле (1), в которой ε(k) – диэлектрическая функция растворителя:

 image002                                                                                    (1)

Приведем формулы для моделей нелокального диэлектрического отклика растворителя (заполняющего все пространство) ε(k), которые мы использовали для расчета W. В литературе эти модели называются “приближениями нескольких (1 или 2) дискретных мод” или “полюсными моделями” [9]. В этих формулах k - волновой вектор, ε1, ε2, ε3 - диэлектрические проницаемости, соответствующие электронным (индекс 1), инфракрасным (индекс 2) и дебаевским (индекс 3) степеням свободы. В формуле (2) λ2, λ3 - корреляционные длины, а в (3) – единственная корреляционная длина λ3 – статическая диэлектрическая проницаемость. Численные значения диэлектрических проницаемостей для воды: ε1 = 1.8, ε2 = 5, ε3 = 78.5, а корреляционных длин: λ2 = 1 Å, тогда как величина наибольшей из корреляционных длин λ3 обычно используется в качестве подгоночного параметра, который для предварительных оценок обычно принимается равным 3Å [9]. Формула для двухполюсной модели ε(k) диэлектрической функции растворителя согласно [7] имеет вид:

 image004                                                                            (2)

Для качественных оценок часто используется одномодовая модель ε(k) [8], которая получается пренебрежением дисперсии диэлектрического отклика в промежуточном интервале длин волн: ε2 = ε1. Тогда формула (2) переходит в формулу:

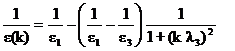   image006                                                                              (3)

Модель размытой борновской сферы. Для случая, когда не учитывается эффект вырезания объема иона функция ρ(k) в подынтегральном выражении (1) является Фурье образом плотности распределения заряда иона ρSBS(r), где r – расстояние от центра иона, а ρSBS(r) - плотность заряда в SBS модели работы [1] (модель размытой борновской сферы):

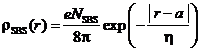image008                                                                                            (4a) Фурье образ ρKS(k) функции ρSBS(r), определяемой по формуле (4а) имеет вид [1]: image010                     (4b) В формулах (4a) и (4b) e – заряд электрона, a – координата максимума плотности распределения заряда иона, η -  параметр, характеризующий ширину размытия заряда. Нормировочный параметр NSBS рассчитывается как: image012                                                                                     (5)

Учет эффекта вырезания растворителя из объема, занятого ионом. Нами был разработан метод расчета энергии сольватации иона W для случая, когда учитывается эффект вырезания объема иона радиуса ri­ из растворителя. В этом методе надо часть заряда иона eNint, находящуюся внутри борновской сферы радиуса ri перенести на саму сферу. При этом распределение части заряда иона eNext, проникающего в растворитель за пределы сферы радиуса ri, по-прежнему определяется по формуле (4). Тогда функция ρ(k) в подынтегральном выражении (1) является Фурье образом плотности распределения ρ­­­VR(r), где ρ­­­VR определяется как:

image014                                                                                (6) где Nint - доля заряда иона внутри борновской сферы, рассчитываемая как: image016                               (7)­ Для вывода формулы (7) мы вычислили интеграл по внутренней области иона от плотности распределения заряда (4). Для расчета энергий сольватации по формуле (1) было нами было выполнено преобразование Фурье плотности заряда ρVR(r), которая определяется по формуле (6). Фурье образ этого распределения ρVR(k,ri) рассчитывается по формулам (8)-(10): image018                                                                                         (8) в которой функции ρ1(k,ri) и ρ2(k,ri) определяются как: image020                                                                                 (9) image022                                                                  (10) Вспомогательные функции Next(η), D(k), g(k) в формуле (10) определяются как: image024                                                                                                          (11) image026                                                                                                                 (12) image028                                                                                       (13) где f1 и f2 определяются как: image030 , image032                                                  (14)

Функция Next(η), рассчитываемая по формулам (11) и (7), определяет долю заряда иона, находящуюся за пределами борновской сферы иона.

Результаты расчета энергии сольватации. Представленные расчеты (Рис. 1.) выполнены для сравнения вычислений по нашей теории (сплошные кривые), учитывающей эффект вырезания растворителя из объема иона, с вычислениями по теории [1], в которой этот эффект не учитывается (штриховые кривые).

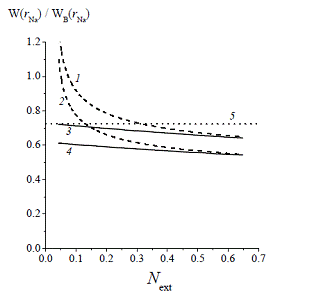
image034

Рис. 1 – Расчет энергии сольватации Na+

 

На Рис. 1 представлены результаты расчета электростатической составляющей энергии сольватации иона Na+ (кривые 1 – 4) в зависимости от доли заряда иона Next, находящегося за пределами борновской сферы радиуса ri = rNa = 1.17 Å. Радиус Na+ взят по шкале Гурари и Адриана [10]. По оси ординат отложено отношение W(rNa), рассчитанной по формуле (1) к WB(rNa), рассчитанной по формуле Борна для локальной среды со статической диэлектрической проницаемостью εS = 78.5:

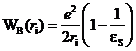image036                                                                                                  (15)

Для модели, не учитывающей эффект вырезания растворителя из объема, занятого ионом (штриховые кривые 1 и 2), энергия сольватации рассчитывалась по формуле (1), в которую подставлялась ρKS(k), рассчитываемая по выражению (4b). Для модели, учитывающей эффект вырезания растворителя из объема, занятого ионом (сплошные кривые 3 и 4), энергия сольватации рассчитывалась по формуле (1), в которую подставлялась ρVR(k), рассчитываемая по выражениям (8)-(14). Величина параметра η для всех расчетов выбиралась равной 0.3. Кривые 1 и 3 рассчитывались для двухполюсной модели (2) диэлектрической функции растворителя, а кривые 2 и 4 для однополюсной модели (3).  Горизонтальная пунктирная линия 5 соответствует экспериментальной энергии сольватации для Na+ (по данным [11] Wexp(Na+) = 424 кДж/моль), а WB(Na+) = 586 кДж/моль (по формуле (15)), то есть Wexp(Na+)/WB(Na+) = 0.724.

Выводы из сравнения расчетов по двум теориям. Как это видно из Рис. 1 (кривые 1, 3 для двухполюсной модели ε(k) и кривые 2, 4 для однополюсной модели ε(k)), энергия сольватации, рассчитанная по нашей теории, учитывающей эффект вырезания объема, меньше, чем по теории, в которой растворитель занимает все пространство [1]. Во всех случаях расчётная величина энергии сольватации W уменьшается при увеличении доли заряда иона, находящейся вне борновской сферы. При переходе от однополюсной модели ε(k) к двухполюсной модели ε(k) значение W увеличивается и для расчетов по нашей теории (переход от кривой 4 к кривой 3) и для теории [1] (переход от кривой 2 к кривой 1). Кривая 4, рассчитанная по нашей теории для однополюсной модели ε(k) ниже экспериментального значения W для Na+ (пунктирная линия 5).  Расчет W по теории [1] для однополюсной модели ε(k) дает согласие с экспериментом при Next = 0.13 (кривая 2). Однако расчет по двухполюсной модели ε(k) для воды более физически обоснован [7, 9]. Кривая 3, рассчитанная по нашей теории для двухполюсной модели ε(k) согласуется с экспериментом для малой величины доли заряда, находящегося вне борновской сферы (Next = 0.04). Расчет W по теории [1] для двухполюсной модели ε(k) дает согласие с экспериментом при значительной доле заряда вне борновской сферы Next = 0.32 (кривая 1).

Главный вывод заключается в том, что расчет энергии сольватации W по нашей теории, учитывающей вырезание из полярной среды полости, в которой находится ион, согласуется (при использовании двухполюсной модели ε(k)) с экспериментальными данными при малых величинах доли заряда иона Next, проникающего в растворитель. Согласие же с экспериментом расчетной величины W по теории работы [1], использующей модель размытого заряда иона и не учитывающей эффекта вырезания растворителя из объема иона, достигается только при больших величинах доли заряда иона, находящейся в растворителе за пределами борновской сферы.

Литература

  1. Kornyshev A. A., Sutmann G. The shape of the nonlocal dielectric function of polar liquids and the implications for thermodynamic properties of electrolytes: A comparative study // J. Chem. Phys. – 1996. - V. 104. – P. 1524-1544.
  2. Dogonadze R., Kornyshev A. A. Polar-solvent structure in theory of ionic solvation // J. Chem. Soc. Faraday Trans. Pt.II. – 1974. - V. 70. – P. 1121-1132.
  3. Рубашкин А. А., Воротынцев М. А., Антипов Е. М., Алдошин С. М. Нелокально-электростатическая теория ионной сольватации: комбинация эффекта переэкранирования в диэлектрическом отклике среды с размытым распределением заряда иона // ДАН – 2015. - Т. 464. - № 1. – С. 56-60.
  4. Vorotyntsev M. A. Model nonlocal electrostatics. II. Spherical interface. // J. Phys. C: Solid State Physics – 1978. - V. 11. – P. 3323-3331.
  5. Basilevsky M. V., Parsons D. F. Nonlocal continuum solvation model with exponential susceptibility // J. Chem. Phys. – 1998. - V.108. – P. 9107-9113.
  6. Hildebrandt A., Blossey R., Rjasanow S., Kohlbacher O., Lenhof H.-P. Novel formulation of nonlocal electrostatics // Phys. Rev. Lett. – 2004. - V. 93. – P. 108104-1 - 108104-4.
  7. Kornyshev A. A., Volkov A.G. On the evaluation of standard Gibbs energies of ion transfer between 2 solvents // J. Electroanal. Chem. – 1984. - V. 180. – P. 363-381.
  8. Kornyshev A. A. Nonlocal screening of ions in a structurized polar liquid - new aspects of solvent description in electrolyte theory // Electrochim Acta. – 1981. - V. 26. – P. 1-20.
  9. Воротынцев М. А., Корнышев А. А. Электростатика сред с пространственной дисперсией. М.: Наука, 1993. С. 20-35.
  10. Gourary B. S., Adrian F. J. Wave Function for Electron-Excess Color Centers in Alkali Halide Crystals // Solid State Phys. – 1960. - V. 10. – P. 127-247.
  11. Fawcett W. R. Thermodynamic parameters for the solvation of monatomic ions in water // J. Phys. Chem. –1999 - V. 103. – P. 11181-11185.

 References

  1. Kornyshev A. A., Sutmann G. The shape of the nonlocal dielectric function of polar liquids and the implications for thermodynamic properties of electrolytes: A comparative study // J. Chem. Phys. – 1996. - V. 104. – P. 1524-1544.
  2. Dogonadze R., Kornyshev A. A. Polar-solvent structure in theory of ionic solvation // J. Chem. Soc. Faraday Trans. Pt.II. – 1974. - V. 70. – P. 1121-1132.
  3. Rubashkin A. A., Vorotyntsev M. A., Antipov E. M., Aldoshin S. M. Nonlocal-electrostatics theory of ion solvation: combination of the overscreening effect in the dielectric response of the medium with a smeared distribution of the ion charge // Dokl. Phys. Chem. – 2015. - V. 464. - №1 – P. 198-201.
  4. Vorotyntsev M. A. Model nonlocal electrostatics. II. Spherical interface. // J. Phys. C: Solid State Physics – 1978. - V. 11. – P. 3323-3331.
  5. Basilevsky M. V., Parsons D. F. Nonlocal continuum solvation model with exponential susceptibility // J. Chem. Phys. – 1998. - V.108. – P. 9107-9113.
  6. Hildebrandt A., Blossey R., Rjasanow S., Kohlbacher O., Lenhof H.-P. Novel formulation of nonlocal electrostatics // Phys. Rev. Lett. – 2004. - V. 93. – P. 108104-1 - 108104-4.
  7. Kornyshev A. A., Volkov A.G. On the evaluation of standard Gibbs energies of ion transfer between 2 solvents // J. Electroanal. Chem. – 1984. - V. 180. – P. 363-381.
  8. Kornyshev A. A. Nonlocal screening of ions in a structurized polar liquid - new aspects of solvent description in electrolyte theory // Electrochim Acta. – 1981. - V. 26. – P. 1-20.
  9. Vorotyntsev M. A., Kornyshev A. A. Elektrostatika sred s prostranstvennoj dispersiej. M.: Nauka, 1993. S. 20-35.
  10. Gourary B. S., Adrian F. J. Wave Function for Electron-Excess Color Centers in Alkali Halide Crystals // Solid State Phys. – 1960. - V. 10. – P. 127-247.
  11. Fawcett W. R. Thermodynamic parameters for the solvation of monatomic ions in water // J. Phys. Chem. –1999 - V. 103. – P. 11181-11185.