ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ ПЛОСКОЙ ТЕРМОУПРУГОЙ ВОЛНЫ

Брыков Н.А.

Ассистент кафедры плазмогазодинамика и теплотехника, Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова, Санкт-Петербург

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ ПЛОСКОЙ ТЕРМОУПРУГОЙ ВОЛНЫ

Аннотация

В статье рассмотрен аналитический и численный метод решения нелинейной задачи распространения плоской термоупругой волны. Состояние тела описывается системой уравнений связанной динамической задачи термоупругости. Аналитическое решение получается с помощью интегрального преобразования Лапласа. Численное решение основано на использовании метода конечных разностей. В статье изложена неявная трехслойная пятиточечная схема для метода прогонки. Представлены результаты аналитического и численного расчета.

Ключевые слова: связанная задача термоупругости, термоупругая волна, метод прогонки.

Brykov N.A.

Assistant of the Department of heat engineering and plasmagasdynamic, Baltic State Technical University «VOENMEH» named after D.F. Ustinov, St. Petersburg

NUMERICAL MODELING OF THE PROPAGATION OF THERMOELASTIC WAVES

Abstract

The article describes a numerical method for solving a nonlinear problem of propagation of a plane thermoelastic waves. Body condition is described by the equations of dynamic thermoelasticity related problem. Presents an analytical solution to the problem of thermoelasticity. The analytical solution is obtained by Laplace transform. The numerical solution is based on the finite difference method. The article presented implicit three-layer scheme for a five-point sweep method. The results of the analytical and numerical calculation.

Keywords: problem of thermoelasticity, thermoelastic waves, sweep method.

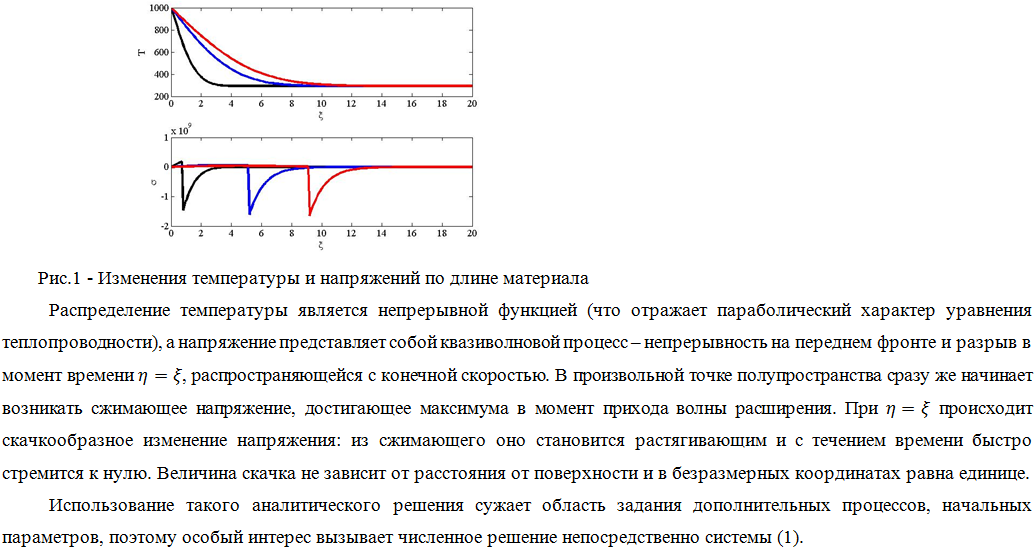
Литература

1. Новацкий В. Динамические задачи термоупругости. Пер. с польск. под ред. Г. С. Шапиро, М.: Мир, 1970. – 256 с.
2. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Наука, 1978. – 532 с.

References

1. Novackij V. Dinamicheskie zadachi termouprugosti. Per. s pol'sk. pod red. G. S. Shapiro, M.: Mir, 1970. – 256 s.
2. Samarskij A.A., Nikolaev E.S. Metody reshenija setochnyh uravnenij. M.: Nauka, 1978. – 532 s.