БАЛАНСОВАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ЛЕСНЫХ ГАРЕЙ
Бутусов О.Б.1, Редикульцева Н.И.2, Никифорова О.П.3
1ORCID: 0000-0003-1361-2121, Доктор физико-математических наук, Московский государственный машиностроительный университет (МАМИ), 2Кандидат технических наук, Московский гуманитарный университет, 3Кандидат технических наук, Государственный университет управления
БАЛАНСОВАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ЛЕСНЫХ ГАРЕЙ
Аннотация
Предложена интегральная математическая модель, описывающая суммарный баланс площадей зарастающих и вновь образующихся гарей. Модель учитывает различие между низовыми и верховыми пожарами. Количество возникающих лесных пожаров моделируется с помощью Пуассоновского потока. Размеры площадей пожара описываются с помощью случайной величины, распределенной по экспоненциальному закону. Параметризация и идентификация модели была проведена на основе статистических данных о площадях лесных пожаров и площадях лесных гарей. Результаты моделирования находятся в удовлетворительном соответствии с статистическими данными.
Ключевые слова: математическая модель, лесные пожары, зарастание гарей, идентификация модели.Butusov O.B.1, Redikultseva N.I.2, Nikiforova O.P.3
1ORCID: 0000-0003-1361-2121, PhD in Physics and Mathematics, Moscow State University of Mechanical Engineering (MAMI), 2PhD in Engineering, Moscow University for the Humanities, 3PhD in Engineering, State University of Management
BALANCE MATHEMATICAL MODEL OF BURNT-OUT FORESTS AREAS DYNAMICS
Abstract
The article put forward mathematical model using total balance between growing up and new burnt out areas. Model considers difference between creeping and crown fires. Model uses Poisson statistics to simulate number of fires. The article considers the size of fire area as exponential probability value. The model identification had been carried out using statistical data on forest fires and burnt out areas. The results of simulation is in good agreement with statistical data.
Keywords: mathematical model, forest fires, growing of burnt out areas, model identification.В статье предложена вероятностная модель лесных пожаров и зарастания гарей. Описание гидродинамической модели лесных пожаров можно найти в [1]. Классические методы моделирования лесных пожаров проанализированы в обзоре [2]. Описание современных методов моделирования можно найти в статье [3]. Среди работ, посвященных моделированию зарастания гарей отметим работы Черкашина А.К. [4], а также работу [5], в которой использована модель, основанная на теории скрытых Марковских моделей.
Лесные пожары наносят огромный и невосполнимый ущерб природным и материальным ресурсам. По данным [4] эколого-экономический ущерб от пожара определяется в зависимости от площади участка выгоревшего леса, совокупности видов растений и животных, пострадавших от пожара, экологической и хозяйственной ценности пород деревьев на этом участке. Например, ущерб от лесных пожаров в 2005 году составил 2,8 млрд. рублей. Произошло 896 лесных пожаров, из них 44 крупных пожара. Выгорело 96300 гектаров лесов. Потеряно 2,6 млн. кубометров древесины (ущерб составил 251,8 млн. рублей). Огнем уничтожено 4240 га молодняков (ущерб - 58,2 млн. рублей). При этом ущерб от уничтожения или повреждения лесной подстилки, почвы, мха, сенокосных и пастбищных угодий составил 2,4 млрд. рублей.
Согласно [1] лес представляет собой фитоценоз, имеющий многоярусную структуру, что является следствием сосуществования растений различных видов и возраста и наличием отпада. В результате детального анализа работ по моделированию лесных пожаров в [1] предложена классификация слоев фитоценоза, учет которых необходим для адекватного математического моделирования лесных пожаров:
- Подстилка толщиной 2-5 см;
- Мох, лишайники и отпад толщиной 10-20 см;
- Кустарнички толщиной 10-20 см;
- Травянистые растения, толщина слоя которых меняется в пределах 0,1-0,8 м;
- Кустарники высотой до 2 м;
- Совокупность крон молодых деревьев (подроста) высотой до 6 м;
- Полог древостоя – совокупность крон взрослых деревьев, имеющих высоту h3 до 25 м и высоту нижней границы крон h2 1-7 м;
- Приземный слой атмосферы высотой до 150-200 м;
- Планетарный пограничный слой, высота которого 1,502 км.
Эта девяти ярусная модель вертикальной структуры лесного биогеоценоза является наиболее полной.
С точки зрения механики, лесной биогеоценоз представляет собой некоторый конкретный объем сплошной многофазной среды. В числе фаз: исходное органическое вещество, вода в жидко-капельном состоянии и воздух.
Среда многомасштабная и имеет неоднородную структуру по вертикальному и горизонтальному направлениям.
Для упрощения модели леса целесообразно объединять некоторые ярусы и рассматривать ярусы объединенных слоев как однородную структуру. В этом случае среда будет кусочно-однородной. Другой подход состоит в том, что объемные доли фаз задаются как непрерывные функции, координаты которых, отсчитываются от подстилающей поверхности.
При моделировании лесного пожара необходимо учитывать, что наиболее интенсивные процессы происходят в зоне лесного пожара, называемой фронтом лесного пожара, который распространяется с некоторой скоростью по территории, покрытой лесом. Эта скорость определяется процессами переноса массы и энергии, а также физико-химическими процессами – сушкой, пиролизом и горением газообразных и конденсированных продуктов пиролиза лесных горючих материалов (ЛГМ). Пиролизом называется расщепление при высокой температуре сложных органических соединений, из которых состоят ЛГМ, на более простые.
В [1] сформулирован универсальный механизм распространения лесных пожаров, который в дальнейшим был подтвержден экспериментальными исследованиями. Любой пожар распространяется за счет передачи выделившегося во фронте пожара тепла путем конвекции и переноса горящих частиц к свежей порции органической массы, в результате чего происходит ее нагрев, сушка и пиролиз. Затем летучие и конденсированные продукты пиролиза сгорают, что вызывает перемещение фронта пожара с выделением тепла, и процесс повторяется в указанном порядке до тех пор, пока в зоне пожара не выгорит весь запас органической массы.
Пожары подразделяются на низовые и верховые. Низовые пожары – это наиболее распространенный вид лесных пожаров. Пожары этого вида возникают не только в лесу, но и в степи, и в тундре. Возникают низовые пожары от локальных очагов огня. Причинами возгорания могут быть как природные причины (так называемые «сухие грозы»), так и возгорания, связанные с деятельностью человека. Анализу условий возникновения, распространения и затухания низовых лесных пожаров посвящено множество работ [1,6,7].
Исследование структуры фронта низового пожара, рассмотренного в работах [8], который распространялся в отсутствии ветра по горизонтальному слою отпада, состоящему из хвои сосны, показало, что в соответствии с универсальной схемой горения движущей силой низового пожара являются процессы разогрева, сушки и пиролиза ЛГМ.
Верховые пожары относятся к виду наиболее быстро распространяющихся и поэтому наиболее опасных лесных пожаров. Согласно [6, 9] существует две основные причины возникновения верховых пожаров:
- Переход низового лесного пожара в верховой;
- Воспламенение сухостойных деревьев, а также полога леса в результате «сухих гроз».
В [6, 9] подробно проанализировано влияние структуры леса, влагосодержания и запаса ЛГМ в пологе леса и почвенном покрове на возникновение верховых лесных пожаров. На основе анализа опытных данных установлено, что на переход низового пожара в верховой сильное влияние оказывает скорость ветра [9]. В Институте леса и древесины СО АН СССР были выполнены специальные экспериментальные исследования по изучению процессов перехода низового лесного пожара в верховой [10, 11]. В результате было установлено, что температура в нижней части крон деревьев меняется в пределах от 370 до 1500 град. К. Также установлено, что при всех наблюдавшихся переходах низового пожара в верховой зарегистрированы пульсации температуры с амплитудой в районе 1200 град. К.
Из зарубежных исследований проблемы перехода низового лесного пожара в верховой следует отметить фундаментальные работы немецкого ученого Ван-Вагнера [12]. Согласно этим работам, основными параметрами, определяющими переход низового лесного пожара в верховой пожар, являются следующие три характеристики полога древостоя:
- Высота нижней границы полога леса h1-h0 над надпочвенным покровом высотой h0;
- Плотность лесных горючих материалов;
- Влагосодержание лесных горючих материалов.
В [12] установлено, что переход низового пожара в верховой происходит при высоте пламени равной высоте нижней границы крон деревьев и температуре ЛГМ в нижней части крон деревьев в районе 1200 град. К. Кроме того, важным параметром перехода является то количество энергии, которое необходимо передать ЛГМ в нижней части кроны дерева для их возгорания.
Рассмотрим теперь основные положения вероятностной балансовой модели лесных пожаров, предложенной в данной статье.
Введем интенсивность потока случайного процесса возникновения лесных пожаров
где ![]() количество пожаров на интервале
количество пожаров на интервале ![]() , M[ ] — обозначает математическое ожидание.
, M[ ] — обозначает математическое ожидание.
Для пуассоновского процесса ![]() — вероятность события, t — текущий момент времени, τ — временной интервал, для которого оценивается число пожаров, k — количество пожаров на интервале
— вероятность события, t — текущий момент времени, τ — временной интервал, для которого оценивается число пожаров, k — количество пожаров на интервале ![]() , — параметр распределения Пуассона.
, — параметр распределения Пуассона.
Примем предположение об экспоненциальном распределении площадей пожаров ![]() , где s — площадь пожара, μ — параметр экспоненциального распределения, равный обратной величине средней площади пожара
, где s — площадь пожара, μ — параметр экспоненциального распределения, равный обратной величине средней площади пожара ![]() , где sm — средняя площадь пожара. При этом совместная плотность распределения вероятностей будет равна
, где sm — средняя площадь пожара. При этом совместная плотность распределения вероятностей будет равна ![]() . Суммарную площадь пожаров найдем с учетом деления лесных пожаров на низовые и верховые как математическое ожидание
. Суммарную площадь пожаров найдем с учетом деления лесных пожаров на низовые и верховые как математическое ожидание
где Sf — математическое ожидание суммарной площади пожаров, b12 — вероятность перехода пожара в категорию верховых, индексы 1, 2 обозначают соответственно низовой и верховой пожары.
Рассмотрим математическую модель зарастания гарей. Предположим, что время зарастания гарей T подчиняется экспоненциальному закону распределения ![]() , где: ν — параметр экспоненциального распределения, равный обратной величине среднего времени зарастания гарей
, где: ν — параметр экспоненциального распределения, равный обратной величине среднего времени зарастания гарей ![]() , tm — среднее время зарастания гарей.
, tm — среднее время зарастания гарей.
Математическое ожидание суммарной площади гарей с учетом процессов их зарастания по истечении времени t можно представить в следующем виде:
Математическое ожидание суммарной площади гарей с учетом процессов их зарастания по истечении времени t можно представить в следующем виде:
где Sg2 — математическое ожидание суммарной площади гарей, ![]() - ступенчатая функция, t — время, прошедшее с момента образования гари, Т – случайная величина, описывающая время зарастания гари. После интегрирования (3) принимает следующий вид
- ступенчатая функция, t — время, прошедшее с момента образования гари, Т – случайная величина, описывающая время зарастания гари. После интегрирования (3) принимает следующий вид
где ![]() — суммарная площадь насаждений, погибших за t лет до текущего момента. Введем следующее обозначение для площади насаждений погибших за d лет до текущего момента
— суммарная площадь насаждений, погибших за t лет до текущего момента. Введем следующее обозначение для площади насаждений погибших за d лет до текущего момента ![]() , где p — год, в который фиксируется площадь гарей, Zp-d — доля погибших насаждений из общей площади пожаров, за d лет до текущего момента,
, где p — год, в который фиксируется площадь гарей, Zp-d — доля погибших насаждений из общей площади пожаров, за d лет до текущего момента, ![]() статистические параметры, описанные выше, для того же периода, Sf (p-d) - математическое ожидание площади пожаров за d лет до текущего момента.
статистические параметры, описанные выше, для того же периода, Sf (p-d) - математическое ожидание площади пожаров за d лет до текущего момента.
Для того чтобы получить суммарную площадь гарей на момент p необходимо просуммировать площади гарей образованных в результате пожаров в течение заданного периода времени с учетом их зарастания:
где Sf (t) - площадь пожаров для года t, r – время зарастания гари.
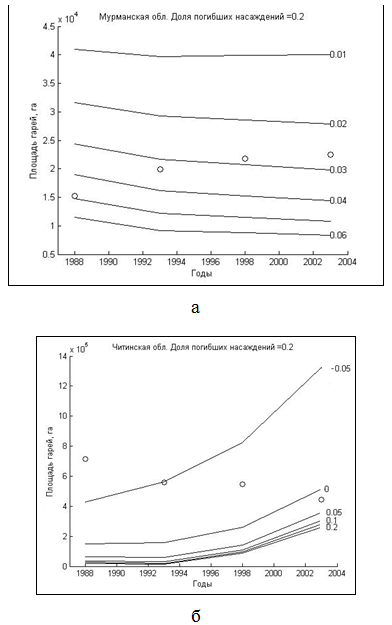
Анализ статистических данных показывает, что ![]() . Второй параметр модели скорость зарастания v является свободным параметром. На рис.1а показаны результаты моделирования баланса площадей пожаров и гарей при разных скоростях зарастания в лесах Мурманской обл., а на рис.1б представлена аналогичная динамика для лесов Читинской обл. Результаты, полученные для Мурманской обл., могут быть согласованы с данными о площадях гарей. Из рис.1а следует, что скорость зарастания гарей в Мурманской обл.
. Второй параметр модели скорость зарастания v является свободным параметром. На рис.1а показаны результаты моделирования баланса площадей пожаров и гарей при разных скоростях зарастания в лесах Мурманской обл., а на рис.1б представлена аналогичная динамика для лесов Читинской обл. Результаты, полученные для Мурманской обл., могут быть согласованы с данными о площадях гарей. Из рис.1а следует, что скорость зарастания гарей в Мурманской обл. ![]() . В то же время для лесов Читинской обл. скорость зарастания отрицательная
. В то же время для лесов Читинской обл. скорость зарастания отрицательная ![]() . Последнее указывает на несогласованность статистических данных по площадям пожаров и гарей.
. Последнее указывает на несогласованность статистических данных по площадям пожаров и гарей.
Рис.1 - Динамика площадей гарей в лесах Мурманской области при разных скоростях зарастания (точками отмечены статистические данные)
Выводы
- Разработаны вероятностные одно- и двух параметрические модели баланса площадей пожаров и гарей.
- Для лесов Мурманской обл. проведена идентификация скорости зарастания гарей, в результате которой показана адекватность статистических данных по лесным пожарам и гарям.
- Невозможность идентификации скорости зарастания гарей для лесов Читинской обл. может свидетельствовать о несогласованности статистических данных по площадям лесных пожаров и гарей.
Литература
- Гришин А.М. Математическое моделирование лесных пожаров и новые способы борьбы с ними. — Новосибирск: Наука, Сиб. отд-ние, 1992. — 408с.
- Perry G.L.W. Current approaches to modeling the spread of wildland fire: a review // Progress in Physical Geography. — 1998. — v.22. — N 2. — P.222-245.
- Ohgai A., Y.Gohnai, S.Ikaruga, M.Murakami, K.Watanabe. Cellular Automata Modeling for Fire Spreading as a Tool to Aid Community-Based Planning for Disaster Mitigation // Advances in Design & Decision Support Systems in Architecture and Urban Planning. — Dordrecht: Kluwer Academic Publishers, 2004. — ISBN: 1-4020-2408-8, — P.193-209.
- Черкашин А.К. Модели естественной и антропогенной динамики лесных ресурсов // Планирование и прогнозирование природно-экономических систем, Под. ред. Гурман В.И., Константинов Г.Н. — Новосибирск, Наука, 1984. — 46-94.
- Rodriguez F., Bautista S. 2006. Modelos ocultos de Markov para el analisis de patrones espaciales // Ecosistemas. — 2006. — N 3. — P.1-8.
- Курбатский Н.П. Классификация лесных пожаров // Вопросы лесоведения. – Красноярск: ИЛиД СО АН СССР, 1970. – 490 с.
- Дорррег Г.А. Математические модели динамики лесных пожаров. – Москва: Лесная промышленность, 1979. – 243 с.
- Сухнин А.И. Температурное поле при распространении пламени по хвои // Проблемы лесной пирологии. – Красноярк: ИЛиД СО АН СССР, 1975. - 230 с.
- Сафронов М. А., Вакуров А. Д. Огонь в лесу. – Новосибирск: Наука, 1981. – 325с.
- Исаков Р.В. Об условиях возникновения лесных пожаров // Прогнозирование лесных пожаров. – Красноярск: Институт леса и древесины СО АН СССР,-1978. – 164с.
- Валендик Э.Н., Исаков З.В. Об интенсивности лесного пожара. – Красноярск: Институт леса и древесины СО АН СССР,-1978. – 190с.
- Van Wagner C.E. Fire behavior mechanisms in a Red Pine Plantation: Ottawa: Field and Laboratory Ewidence, 1968. – Report № 1229. – 69 р.
References
- Grishin A.M. Matematicheskoe modelirovanie lesnyh pozharov i novye sposoby bor'by s nimi. — Novosibirsk: Nauka, Sib. otd-nie, 1992. — 408s.
- Perry G.L.W. Current approaches to modeling the spread of wildland fire // Progress in Physical Geography. – 1998. – V.22. - N2. – P.222-245.
- Ohgai A., Y.Gohnai, S.Ikaruga, M.Murakami, K.Watanabe. Cellular automata modeling for fire spreading as a tool to aid community-based planning for disaster mitigation. Advances in Design & Decision Support Systems in Architecture and Urban Planning. – Dordrecht: Kluwer Academic Publishers, 2004. – P.193-209.
- Cherkashin A.K. Modeli estestvennoj i antropogennoj dinamiki lesnyh resursov // Planirovanie i prognozirovanie prirodno-jekonomicheskih sistem, Pod. red. Gurman V.I., Konstantinov G.N. — Novosibirsk, Nauka, 1984. — 46-94.
- Rodriguez F, Bautista S (2006) Modelos ocultos de Markov para el analisis de patrones espaciales // Ecosistemas. – 2006. - N 3. – P.1-8.
- Kurbatskij N.P. Klassifikacija lesnyh pozharov // Voprosy lesovedenija. – Krasnojarsk: ILiD SO AN SSSR, 1970. – 490 s.
- Dorrreg G.A. Matematicheskie modeli dinamiki lesnyh pozharov. – Moskva: Lesnaja promyshlennost', 1979. – 243 s.
- Suhnin A.I. Temperaturnoe pole pri rasprostranenii plameni po hvoi // Problemy lesnoj pirologii. – Krasnojark: ILiD SO AN SSSR, 1975. - 230 s.
- Safronov M. A., Vakurov A. D. Ogon' v lesu. – Novosibirsk: Nauka, 1981. – 325s.
- Isakov R.V. Ob uslovijah vozniknovenija lesnyh pozharov // Prognozirovanie lesnyh pozharov. – Krasnojarsk: Institut lesa i drevesiny SO AN SSSR,-1978. – 164s.
- Valendik Je.N., Isakov Z.V. Ob intensivnosti lesnogo pozhara. – Krasnojarsk: Institut lesa i drevesiny SO AN SSSR, 1978. – 190s.
- Van Wagner C.E. Fire behavior mechanisms in a Red Pine Plantation. – Ottawa: Field and Laboratory Ewidence, 1968. – Report № 1229. – 69 р.