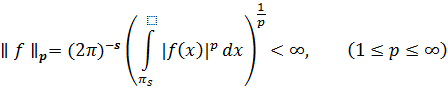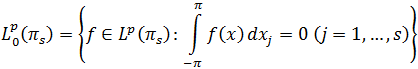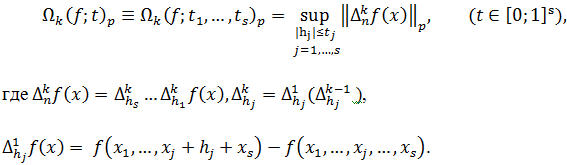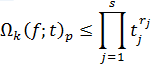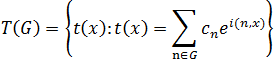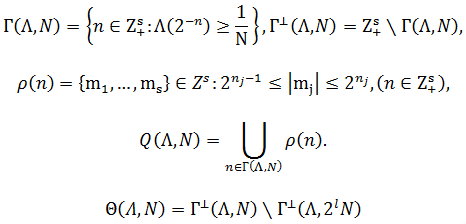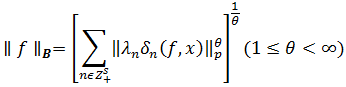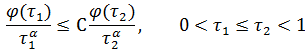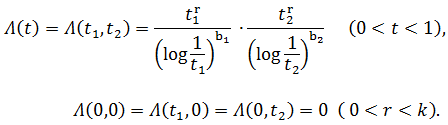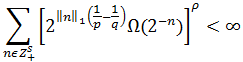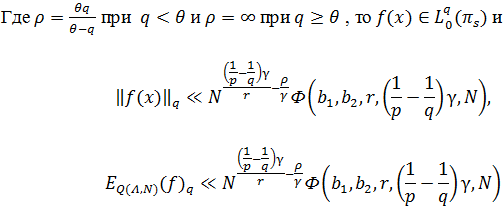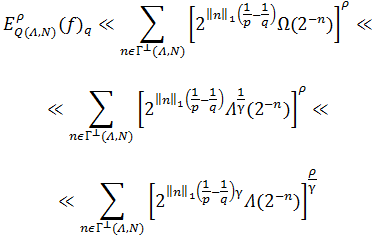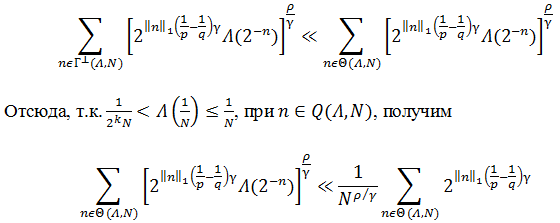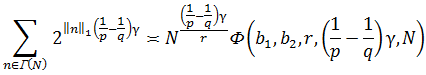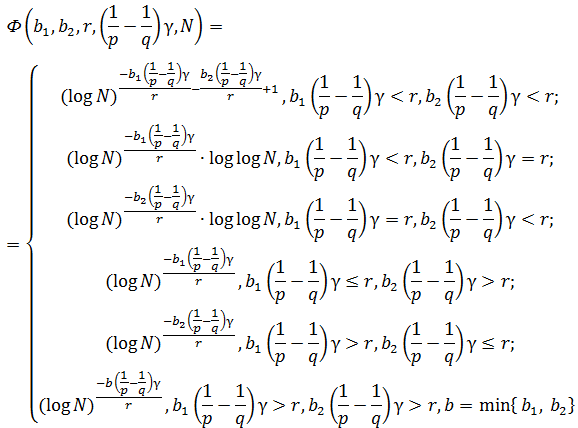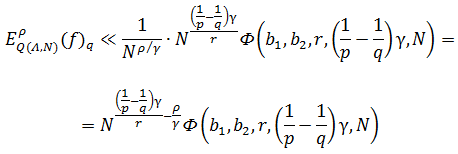ОЦЕНКИ НАИЛУЧШИХ ПРИБЛИЖЕНИЙ ФУНКЦИИ СПЕКТРОМ ИЗ ГИПЕРБОЛИЧЕСКИХ КРЕСТОВ
Турова М. Е.
Магистрант, Казахский Национальный Университет им. Аль-Фараби
ОЦЕНКИ НАИЛУЧШИХ ПРИБЛИЖЕНИЙ ФУНКЦИИ СПЕКТРОМ ИЗ ГИПЕРБОЛИЧЕСКИХ КРЕСТОВ
Аннотация
В статье отражен процесс получения новой точной оценки наилучшего приближения тригонометрическими полиномами спектром «типа гиперболических крестов» в пространстве Бесова, путем использования уже известных оценок и доказанных результатов. Спектр приближающих полиномов лежит в множествах, порожденных поверхностями уровня функции Ω (t) . Эти множества являются обобщением гиперболических крестов на случай произвольного Ω (t)
Ключевые слова: наилучшее приближение, оценка наилучшего приближения, модуль гладкости, модуль непрерывности, гиперболический крест.
Turova M. E.
Postgraduate student, Al-Farabi Kazakh National University
ESTIMATION OF THE BEST APPROXIMATION OF THE SPECTRUM OF THE HYPERBOLIC CROSSES
Abstract
The article describes the process of getting a new accurate estimate of the best approximation by trigonometric polynomials range "type of hyperbolic crosses" in the Besov space, through the use of known and proven assessment results. The range approximating polynomials lies in the set generated by the level surfaces of the function Ω (t). These sets are a generalization of hyperbolic crosses to arbitrary Ω (t).
Key words: the best approximation, assessment of best approximation, modulus of smoothness, modulus of continuity, hyperbolic cross.
Объектом исследования являются оценки наилучших приближений функции спектром «типа гиперболических крестов». Очевидно, актуальность этой темы напрямую определяется численным анализом, в особенности с развитием компьютерных технологий. Данная тема органически связана с дальнейшим развитием задач оценки наилучших приближений функции спектром «типа гиперболических крестов», неравенств типа Бернштейна и Никольского, теории восстановлений и приближений. Тем самым, приходим к большому количеству новых задач.
В данной статье мы рассмотрим приближения тригонометрическими полиномами, гармоники которых лежат в множествах, порожденных поверхностями уровня мажоранты Ω (t) Используя уже известные результаты и новые оценки, получим оценку наилучшего приближения функции спектром «типа гиперболических крестов».
Введем некоторые обозначения. Пусть ![]() - s-мерный куб,
- s-мерный куб, ![]() – множество всех измеримых
– множество всех измеримых ![]() - периодических по каждой из s переменных функций
- периодических по каждой из s переменных функций ![]() таких, что
таких, что
пусть так же
Для подмножества B евклидова пространства ![]() через B0 и B+ обозначим множества, состоящие из всех элементов
через B0 и B+ обозначим множества, состоящие из всех элементов ![]() , каждая компонента которых неотрицательна и положительна соответственно. Через
, каждая компонента которых неотрицательна и положительна соответственно. Через ![]() , как обычно, обозначим целочисленную решетку
, как обычно, обозначим целочисленную решетку ![]() . Для
. Для ![]() положим
положим ![]() .
.
Для ![]() определен смешанный модуль гладкости порядка
определен смешанный модуль гладкости порядка ![]()
Для данных чисел ![]() класс Никольского
класс Никольского ![]() состоит, по определению, из всех функций
состоит, по определению, из всех функций ![]() , таких, что для смешанного модуля гладкости порядка
, таких, что для смешанного модуля гладкости порядка ![]() выполнено
выполнено
Если ![]() , то через
, то через ![]() обозначают лучшее приближение (в
обозначают лучшее приближение (в ![]() ) функции
) функции ![]() полиномами из
полиномами из ![]() , где
, где ![]() - это конечное множество точек из
- это конечное множество точек из ![]() , а
, а
В нашей работе спектр G будет задан посредством непрерывной на ![]() функции
функции ![]() , неубывающей по каждой переменной при фиксированных остальных и такой, что
, неубывающей по каждой переменной при фиксированных остальных и такой, что ![]() и
и ![]() смотря по тому
смотря по тому ![]() или
или ![]() . В связи с этим определим следующие множества
. В связи с этим определим следующие множества ![]()
Будем считать, что ![]() удовлетворяет условию (S). Это означает, следующее.
удовлетворяет условию (S). Это означает, следующее.
Пусть ![]() - последовательность чисел. Через
- последовательность чисел. Через ![]() обозначим пространство функций
обозначим пространство функций ![]() для которых конечна полунорма
для которых конечна полунорма
Функции одного переменного ![]() удовлетворяют условию (S), если
удовлетворяют условию (S), если ![]() почти возрастает при некотором
почти возрастает при некотором ![]() , т.е. найдется число
, т.е. найдется число ![]() , не зависящее от
, не зависящее от ![]() и
и ![]() , такое, что
, такое, что
Замечание 1. Если ![]() удовлетворяет условию (S) с некоторыми
удовлетворяет условию (S) с некоторыми ![]() по переменным
по переменным ![]() , то взяв
, то взяв ![]() , можно утверждать, что
, можно утверждать, что ![]() удовлетворяет условию (S) при этом значении по всем переменным.
удовлетворяет условию (S) при этом значении по всем переменным.
В дальнейшем в качестве мажорантной функции ![]() , которая отвечает за спектр приближающего полинома, возьмем
, которая отвечает за спектр приближающего полинома, возьмем
Здесь рассматриваются логарифмы по основанию 2.
Также положим
Для некоторого γ, такого что ![]() . Ясно, что
. Ясно, что ![]() обладает свойствами смешанного модуля гладкости порядка k.
обладает свойствами смешанного модуля гладкости порядка k.
Теорема. Пусть ![]() . И пусть
. И пусть ![]() и
и ![]() определены как в (1) и (2) соответственно и
определены как в (1) и (2) соответственно и ![]() .
.
Доказательство. Т.к. ![]() , то по теореме 1.4.2 из [3, стр.78] имеем
, то по теореме 1.4.2 из [3, стр.78] имеем
По лемме 2 из [2, стр. 111] получаем
Теперь, применяя Лемму 2.5 [3, стр. 91] при ![]() получаем:
получаем:
где
Отсюда следует:
Таким образом, мы получили новую оценку функции спектром «типа гиперболических крестов» в пространстве Бесова.
Литература
- Коляда В.И. Теорема вложения и неравенства разных метрик для наилучших приближений //Матем. сборник, 1977, Т.102, № 2, С.195- 215.
- Пустовойтов Н. Н. Приближение многомерных функций с заданной мажорантой смешанных модулей непрерывности // Математические заметки. 1999. Т 65. №1. С.107-117.
- Сихов М. Б. О некоторых задачах многомерной теории приближений разных метрик // Докторская диссертация на соискание степени доктора физико-математических наук. Казань, 2010. 186 с.
- Сихов М.Б., Темиргалиев Н. Новые задачи об аппроксимативных возможностях полиномов по ортогональным системам с произвольным спектром //Материалы республиканской научно-практической конференции «Проблемы применения современных математических методов и компьютерных технологий в инженерных науках и строительстве», посвященной 60-летию со дня рождения К.С. Бижанова. 17 августа 2012 г. С.406. Астана 2013г. С. 149-154.
- Сихов М.Б., Темиргалиев Н. Об аппроксимативных возможностях полиномов по ортогональным системам с произвольным спектром // Материалы 3-конгресса математиков тюркоязычных стран, Алматы, 30 июнь-4 июль, 2009 г. С. 140.
References
- Koljada V.I. Teorema vlozhenija i neravenstva raznyh metrik dlja nailuchshih priblizhenij //Matem. sbornik, 1977, T.102, № 2, S.195- 215.
- Pustovojtov N. N. Priblizhenie mnogomernyh funkcij s zadannoj mazhorantoj smeshannyh modulej nepreryvnosti // Matematicheskie zametki. 1999. T 65. №1. S.107-117.
- Sihov M. B. O nekotoryh zadachah mnogomernoj teorii priblizhenij raznyh metrik // Doktorskaja dissertacija na soiskanie stepeni doktora fiziko-matematicheskih nauk. Kazan', 2010. 186 s.
- Sihov M.B., Temirgaliev N. Novye zadachi ob approksimativnyh vozmozhnostjah polinomov po ortogonal'nym sistemam s proizvol'nym spektrom //Materialy respublikanskoj nauchno-prakticheskoj konferencii «Problemy primenenija sovremennyh matematicheskih metodov i komp'juternyh tehnologij v inzhenernyh naukah i stroitel'stve», posvjashhennoj 60-letiju so dnja rozhdenija K.S. Bizhanova. 17 avgusta 2012 g. S.406. Astana 2013g. S. 149-154.
- Sihov M.B., Temirgaliev N. Ob approksimativnyh vozmozhnostjah polinomov po ortogonal'nym sistemam s proizvol'nym spektrom // Materialy 3-kongressa matematikov tjurkojazychnyh stran, Almaty, 30 ijun'-4 ijul', 2009 g. S. 140.