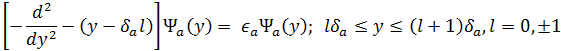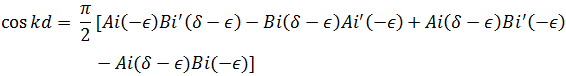МОДЕЛИРОВАНИЕ ЗОННОЙ СТРУКТУРЫ СВЕРХРЕШЕТКИ С ТРЕУГОЛЬНЫМИ БАРЬЕРАМИ

Богословская Н. М.¹, Вдовин С. И.², Лобаев А.Н.³

¹Кандидат технических наук, доцент, ²Кандидат технических наук, доцент, ³Кандидат физико-математических наук, доцент, Нижегородский государственный технический университет им. Р.Е.Алексеева

МОДЕЛИРОВАНИЕ ЗОННОЙ СТРУКТУРЫ СВЕРХРЕШЕТКИ С ТРЕУГОЛЬНЫМИ БАРЬЕРАМИ

Аннотация

Построена зонная структура пилообразной сверхрешетки. Получен закон дисперсии электронов и дырок для нижних энергетических минизон. Рассмотрено  влияние природы и высоты потенциального барьера на число и ширину энергетических минизон.

Ключевые слова: Сверхрешетка, зонная структура сверхрешеток, закон дисперсии минизон, численное моделирование.

Bogoslovskaya N. M.¹, Vdovin S. I.²,Lobaev A.N.³

¹Candidate of Sciences in Technics, assistant professor, ²Candidate of Sciences in Technics, assistant professor, ³Candidate of Physico-mathematical Sciences, assistant professor, Nizhny Novgorod State Technical University n.a. R.E. Alekseev.

SIMULATION OF BAND SUPERLATTICE STRUCTURE WITH A TRIANGULAR BARRIER

Abstract

The band structure of sawtooth superlattice is built. The dispersion law for electrons and holes to the lower energy minibands is obtained. The influence of the nature and potential barrier height at the number and width of energy minibands is considered.

Key words: Superlattice, band structure of superlattice, dispersion law of minibands, numeric modeling 

В последнее время полупроводниковые сверхрешетки привлекают большое внимание своими оптическими, электрическими и транспортными свойствами /1,2/. Впервые идея о создании сверхрешеток была высказана в работе /3/.

Сверхрешетки представляют собой твердотельные структуры , в которых на электроны, помимо периодического потенциала кристаллической решетки, действует дополнительный потенциал с периодом, значительно превышающим постоянную решетки. Наличие такого потенциала существенно изменяет электронный энергетический спектр системы, вследствие чего  сверхрешетки приобретают ряд характерных свойств, отсутствующих у однородных материалов.

В работе /4/ сообщалось о переходных поляризационных явлениях в пилообразных сверхрешетках р-типа. Пилообразные сверхрешетки образованы из Al_xGa_1-xAs, у которого x линейно изменяется от нуля в начале периода сверхрешетки до некоторой величины x₀ в конце периода, а затем резко падает вновь до нуля. В работе /4/ x₀ = 0,2. Подобное изменение приводит к периодическому линейному изменению энергетической щели. Пилообразные сверхрешетки могут использоваться для регистрации коротких световых импульсов /4/.

В этой работе мы рассчитаем структуру минизон таких сверхрешеток, построим закон дисперсии электронов и дырок для нижних энергетических минизон,  рассмотрим влияние периода и высоты потенциального барьера сверхрешетки на число и ширину энергетических минизон.

Движение носителей тока в пилообразной сверхрешетке в приближении эффективных масс для полупроводников с изотропными и невырожденными энергетическими зонами описывается уравнением Шредингера:

,       где                                              (1)

;                 (2)

m_a(a = e,h) – эффективная масса электрона  (дырки); d – период сверхрешетки;

 F_az – высота потенциального барьера в зоне проводимости (валентной зоне). Известно /5/, что F_h/F_e = 3/17.

Следует отметить, что в уравнении (1) пренебрегли небольшим изменением  эффективной массы носителей тока в зависимости от z.

Простым разделением переменных уравнение (1) сводится к одномерному уравнению Шредингера, описывающему движение электронов (дырок) вдоль оси z в потенциале :

                            (3)

Здесь  – энергия свободного движения носителей тока в плоскости, перпендикулярной оси сверхрешетки.

Так как потенциал V_a(z)(2) периодичен, то и волновая функция ψ_a(z) так же периодична с периодом d:

,

где  Уравнение (3) легко обезразмерить, используя единицы

  в которых (3) примет следующий вид:

Необходимо заметить, что для пилообразной сверхрешетки, рассмотренной в /4/, δ_e и δ_h (для тяжелых дырок) примерно одинаковы (δ_e=11,0; δ_h=11,5).

Уравнение для определения структуры минизон пилообразной сверхрешетки имеет вид:

Здесь Ai(x), Bi(x) – функции Эйри /6/. Для δ≤1, согласно (4), имеется всего одно минизона с законом дисперсии .

При δ<δc (δc=3,0) в пилообразной сверхрешетке также имеется всего одна минизона, ширина которой Δ_l=0,821, ∈_l=1,155 для δ=2. Закон дисперсии носителей тока в этой минизоне описывается формулой:

.

Таблица 1 - Ширина нижней минизоны пилообразной сверхрешетки

Таблица 2 - Число минизон N, положение дна минизон ∈_k  и их ширина Δ_k для различных значений δ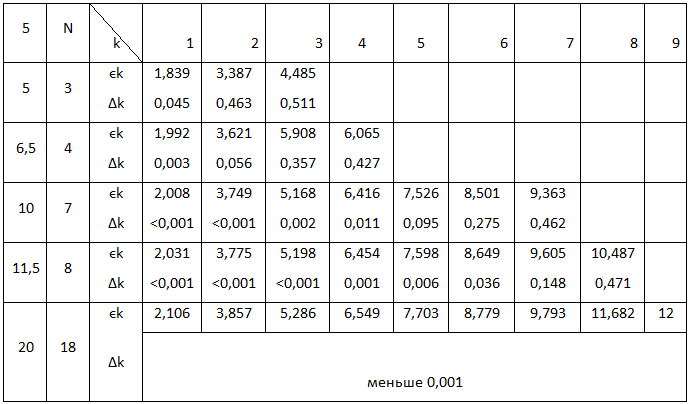

С ростом δ минизоны ∆ экспоненциально убывает (табл.1), а ∈_l стремится к нижнему уровню электрона (дырки) в бесконечно глубокой треугольной яме (т.е. к значению 2,34, которое соответствует первому корню уравнения Ai(-а) = 0 /6/).

При δ>>1 число энергетических минизон в пилообразной сверхрешетке N возрастает при увеличении δ (табл. 2), а ширина нижних (∈<<δ) минизон экспоненциально уменьшается. Таким образом, спектр носителей тока в нижних минизонах пилообразной сверхрешетки анизотропен и является практически двумерным.

Для пилообразной сверхрешетки р-типа, рассмотренной в /4/, оценки энергии Ферми двумерного дырочного газа указывают на возможность заполнения всех дырочных минизон. В этом случае движение дырок становится почти свободным, что подтверждает сделанное в /4/ предположение о том, что в пилообразных сверхрешетках потенциал не влияет на движение дырок.

Литература

1. Esaki L. InAs-GaSb superlattices-synthesized narrow- gap semiconductors and semimetals// Lect. Not. Phys. 1980. Vol.133, №2. – 302-323.
2. Dohler G.H. Doping superlattices ( ‘n-i-p-i Crystals’)// IEEE J. Quant. Electron. 1986. Vol. QE 22, №9, -P. 1682-1685.
3. Келдыш Л.В. О влиянии ультразвука на электронный спектр кристалла // Физика Твердого Тела. – 1962. - Т4, №8. С. 2264-2267.
4. Sercel P. C., Vahala K. J. Analytical formalism for determining quantum-wire and quantum-dot band structure in the multiband envelope-function approximation // Phys. Rev B 1990. Vol..42, №6. P. 3960-3709.
5. Razeghi M., Duchemin J. P. MOCVD growth for heterostructures and two-dimensional electronic systems// Springer Ser. Solid State Sci. - Vol. 53, №1. – P. 100-114.
6. Абрамович М., Стиган И. Справлчник по специальным функциям.- М.: Наука, 1979.-С.50-140.

References

1. Esaki L. InAs-GaSb superlattices-synthesized narrow- gap semiconductors and semimetals// Lect. Not. Phys. 1980. Vol.133, №2. – 302-323.
2. Dohler G.H. Doping superlattices ( ‘n-i-p-i Crystals’)// IEEE J. Quant. Electron. 1986. Vol. QE 22, №9, -P. 1682-1685.
3. Keldysh L.V. O vlijanii ul'trazvuka na jelektronnyj spektr kristalla // Fizika Tverdogo Tela. – 1962. - T4, №8. S. 2264-2267.
4. Sercel P. C., Vahala K. J. Analytical formalism for determining quantum-wire and quantum-dot band structure in the multiband envelope-function approximation // Phys. Rev B 1990. Vol..42, №6. P. 3960-3709.
5. Razeghi M., Duchemin J. P. MOCVD growth for heterostructures and two-dimensional electronic systems// Springer Ser. Solid State Sci. - Vol. 53, №1. – P. 100-114.
6. Abramovich M., Stigan I. Spravlchnik po special'nym funkcijam.- M.: Nauka, 1979.-S.50-140.