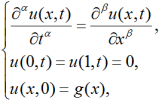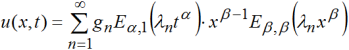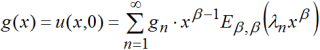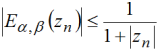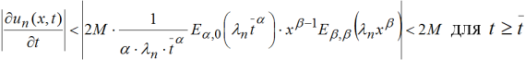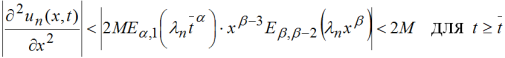КРАЕВАЯ ЗАДАЧА ДЛЯ ОДНОМЕРНОГО ДРОБНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ АДВЕКЦИИ-ДИФФУЗИИ

Исаева Л. М.¹, Эдилова Р.М.²

¹Аспирант, Кафедра высшей математики, Московский государственный строительный университет; ²Ассистент факультета среднего профессионального образования, Грозненский государственный нефтяной университет

КРАЕВАЯ ЗАДАЧА ДЛЯ ОДНОМЕРНОГО ДРОБНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ АДВЕКЦИИ-ДИФФУЗИИ

Аннотация

Рассматривается одна из краевых задач для одномерных дифференциальных уравнений дробного порядка. Используя метод Фурье, в явном виде выписано решение этой задачи. Полученные результаты могут найти применение в теории течения жидкости во фрактальной среде и моделировать изменения в температуре.

Ключевые слова: уравнение дробного порядка, дробная производная, метод Фурье, коэффициенты Фурье, собственные значения и собственные функции, функция Миттаг-Леффлера.

Isaeva L.M.¹, Edilova R.M.²

¹Post-graduate student, Chair of higher mathematics, Moscow State University; ²Assistant of the faculty of secondary vocational education, Grozny state oil University

THE BOUNDARY VALUE PROBLEM FOR THE ONE-DIMENSIONAL FRACTIONAL DIFFERENTIAL EQUATIONS ADVECTION-DIFFUSION

Abstract

Considers one of boundary value problems for one-dimensional differential equations of fractional order. Using the Fourier method, explicitly written the solution to this problem. The results can find application in the theory of fluid flow in a fractal environment and to simulate changes in temperature.

Key words: the equation of fractional order, fractional derivative, Fourier method, the Fourier coefficients, eigenvalues and eigenfunctions, the Mittag-Leffler function.

Использование дробных производных для описания и изучения физических процессов стохастического переноса стало в последние годы одной из популярных областей физики, многие проблемы фильтрации жидкости  и газа в сильно-пористых (фрактальных) средах [1], [2], [3],  приводят также к необходимости изучения краевых задач для уравнений в частных производных дробного порядка. Рассмотрим одну из таких краевых задач  для одномерного дифференциального уравнения дробного порядка:

                                   _{(1)    (2)    (3)}

где  ,  – дробные производные порядков α и β соответственно (0<α<2, 1<β<2).

Имеют место следующая теорема.

Теорема. Функция  является решением задачи (1), (2), (3). Здесь  – известная функция Миттаг-Леффлера, а g_n – соответствующие коэффициенты Фурье  функции g(x) по базису    [1].

Доказательство. Найдем непрерывное в замкнутой области (0≤x≤1, 0≤t≤T) решение однородного дробного дифференциального уравнения

                  (1)

удовлетворяющее условиям (2) и (3).

Для решения этой задачи рассмотрим, как принято в методе разделения переменных [4], сначала основную вспомогательную задачу:

найти решение уравнения (1), не равное тождественно нулю, удовлетворяющее однородным граничным условиям  (2) и представимое в виде

                           (4)

где ω(x) – функция только переменного x, p(t) – функция только переменного t.

Подставляя предполагаемую форму решения (4) в уравнение (1) и производя деление обеих частей равенства на ω(x)p(t), получим:

                  (5)

где λ=const, так как левая часть равенства зависит только от t, а правая – только от x.

Из (5) следует, что

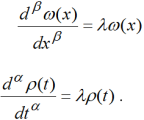                   (6)      (7)

Граничные условия (3) дают:

           (8)

Таким образом, для определения функции ω(x) мы получили задачу о собственных значениях (двухточечную задачу Дирихле)

                         (9)

изученную в работах [1], [5], [6]. В этих работах было показано, что только для собственных значений λ_n, являющихся нулями функции E_β,β(λ), существуют собственные функции задачи (9), равные

                                         (10)

Уравнение  вида (7) рассмотрено в работах  [5], [6], [7],  в которых   показано, что для собственных значений λ_n, являющихся нулями функции E_a,1(λ), существуют собственные функции вида , где g_n – неопределенные пока коэффициенты.

Возвращаясь к основной вспомогательной задаче, видим, что функции

являются частными решениями уравнения (1), удовлетворяющими нулевым граничным условиям (2).

Обратимся теперь к решению задачи (1), (2), (3). Формально составим ряд

                                 (11)

Функция u(x,t) удовлетворяет граничным условиям, так как им удовлетворяют все члены ряда. Требуя выполнения начальных условий, получаем:

                                 (12)

В [8] было показано, что система функций  вида  образует базис в L₂(0;1). Так как базис  не ортогональный, то вместе с системой  будем рассматривать систему  – биортогональную к системе  [9]. Система  – это система собственных функций сопряженной задачи (9) [10].

Теперь неизвестные коэффициенты  можно определить с помощью системы функций :

                         (13)

где (g(x), z_n) – скалярное произведение функций g(x) и z.

Докажем, что для любых 0<x<1 и 0≤t≤T ряд (11) сходится абсолютно. Для достаточно больших по модулю нулей z_n функции E_a,β(z_n) справедлива следующая оценка [11]:

                    (14)

При этом [11],

                         (15)

Тогда, учитывая (14), (15) получаем следующие соотношения:

                                                             (16)

                         (17)

Теперь, согласно (16), (17), оценим (10) по модулю

Рассмотрим мажорирующий ряд , который является сходящимся рядом.

  Из сходимости мажоранты следует сходимость  ряда (11).

Покажем теперь, что при t≥t̅ ≥0 (t̅ – любое вспомогательное число) ряды производных  и   сходятся равномерно. Для этого достаточно показать сходимость рядов   и   ,

так как 0<α<2, 1<β<2.

Сформулируем дополнительные требования, которым должна удовлетворять функция g(x). Предположим сначала, что g(x) ограничена, |g(x)|<M.

Тогда 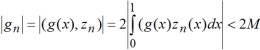, откуда следует, учитывая что  :

Аналогично, учитывая что :

  

Тем самым доказано, что при t>0 ряд (11) представляет собой функцию, дифференцируемую почленно по t и два раза по x, а значит, имеющую производные порядков α и β, так как 0<α<2, 1<β<2.

Итак, задача нахождения первой краевой задачи для одномерного уравнения с нулевыми граничными условиями и непрерывным начальным условием решена полностью.

Литература

1. Нахушев А. М. Дробное исчисление и его применение. // (Физматлит, 2003). 272 с.
2. Алероев Т. С. Краевые задачи для дифференциальных уравнений дробного порядка. // Сиб. электрон. матем. изв. 10, 41-55 (2013).
3. S. Aleroev, M. Kirane, Malik S. A. Determination of a source term for a time fractional diffusion equation with an integral type over-determining condition. // Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 270, pp. 1–16. ISSN: 1072-6691. //URL: htpp://ejde.math.txstate.edu
4. Тихонов А. Н., Самарский А. А. Уравнения математической физики. – М.: Издательство МГУ, 1999. 799 с.
5. Самко С.Г., Килбасс А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. – Минск: Наука и техника, 1987. 688 c.
6. Джрбащян М. М. Краевая задача для дифференциального оператора типа Штурма-Лиувилля дробного порядка /// Известия АН Армянской ССР. Серия «Математика», 5:2 (1970), 71-96.
7. Алероев Т. С., Алероева Х. Т. Об одном классе несамосопряженных операторов, сопутствующих дифференциальным уравнениям дробного порядка. // Изв. ВУЗов, 2014, №10, с. 3-12.
8. Хасамбиев М. В., Алероев Т. С. Краевая задача для одномерного дробного дифференциального уравнения адвекции-диффузии. // Вестник МГСУ №6, 2014, с. 71-76.
9. Aleroev T. S., Aleroeva H. T. A problem on the zeros of the Mittag-Leffler function and the spectrum of a fractional-order differential operator /// Electron. J. Qual. Theory Diff. Equ., № 25, 18 p. (2009).
10. S. Aleroev, M. Kirane, Y.-F. Tang. Boundary-value problems for differential equations of fractional order. // Journal of Mathematical Sciences. Nov. 2013, Volume 194, Issue 5, pp. 499-512.
11. Попов А. Ю., Седлецкий А. М. Распределение корней функций Миттаг-Леффлера. // Современная математика. Фундаментальные направления, 2011, т. 40, с. 3-171.

References

1. Nakhushev A.M. Fractional calculus and its application. - Moscow: Fizmatlit, 2003.
2. Aleroev T. S. Boundary value problems for differential equations of fractional order. // Sib. electron. Mat. Math. 10, 41-55 (2013).
3. S. Aleroev, M. Kirane, Malik S. A. Determination of a source term for a time fractional diffusion equation with an integral type over-determining condition. // Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 270, pp. 1–16. ISSN: 1072-6691. //URL: htpp://ejde.math.txstate.edu
4. Tikhonov A.N., Samarskij A.A. Equations of mathematical physics. – Moscow: Moscow State University Press, 1999. 799 pp.
5. Samko S.G., Kilbass A.A., Marichev O.I. Integrals and derivatives of fractional order, and some applications. - Minsk: Science and Technology, 1987. 688 c.
6. Dzhrbaschyan M.M. Boundary value problem for the differential operator of Sturm-Liouville fractional order /// News of Sciences of the Armenian SSR. Series "Mathematics", 5: 2 (1970), 71-96.
7. Aleroev T.S., Aleroeva H.T. A class of self-adjoint operators associated with differential equations of fractional order. // Math. Universities, 2014, №10, p. 3-12.
8. Hasambiev M.V., Aleroev T.S. Boundary value problem for the one-dimensional differential equation of fractional advection-diffusion. // Herald MGSU №6, 2014, p. 71-76.
9. Aleroev T. S., Aleroeva H. T. A problem on the zeros of the Mittag-Leffler function and the spectrum of a fractional-order differential operator /// Electron. J. Qual. Theory Diff. Equ., № 25, 18 p. (2009).
10. S. Aleroev, M. Kirane, Y.-F. Tang. Boundary-value problems for differential equations of fractional order. // Journal of Mathematical Sciences. Nov. 2013, Volume 194, Issue 5, pp. 499-512.
11. Popov A., AM Sedleckii Distribution of zeros of the Mittag-Leffler. // Contemporary Mathematics. Fundamental direction 2011 m. 40, p. 3-171.