ПОСТРОЕНИЕ И АНАЛИЗ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ GHTLVTNYS[ НА НЕЧЕТКОЙ ЛОГИКЕ

Балашова И.Ю. ¹, Князев В.Н.², Левашко В.В.³

¹Кандидат технических наук, доцент, Пензенский государственный университет; ²Кандидат технических наук, доцент, Пензенский государственный университет; ³Магистрант

ПОСТРОЕНИЕ И АНАЛИЗ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ GHTLVTNYS[ НА НЕЧЕТКОЙ ЛОГИКЕ

Аннотация

В статье рассмотрено – модификация моделей предметных и персональных знаний на основе нечетко-логических математических моделей для их использования при разработке компьютерной обучающей системы.

Ключевые слова: модификация, модель, нечеткая логика.

Balashova I.Yu. ¹, Knjazev V.N. ², Levashko V.V. ³

¹PhD, Associate Professor, Penza State University; ²PhD, Associate Professor, Penza State University; ³Master's degree

PRESENTATION MATHEMATICAL MODEL OF FUZZY LOGIC

Abstract

The article considers - modification models subject and personal knowledge based on fuzzy logic mathematical models for use in developing a computer learning system.

Keywords: modification, model, fuzzy logic.

Проблеме компьютерного обучения в настоящее время отводится большое внимание. В процессе компьютерного обучения участвуют во взаимосвязанной деятельности его субъекты, выполняющие функции педагога и обучаемого. Исходя из этого, компьютерная обучающая система должна содержать знания педагога о составе и структуре учебного предмета (предметные знания) и знания об обучаемом (персональные знания)[1].

Процесс обучения, как процесс творческий, относится к плохо формализуемым процессам. В подобных случаях наиболее целесообразно воспользоваться такими методами, которые специально ориентированы на построение моделей, учитывающих неполноту и неточность исходных данных.

Именно поэтому нечетко-логические модели оказываются наиболее конструктивными при описании предметных и персональных знаний [1, 2].

Большинство известных моделей предметных и персональных знаний учитывают только одну характеристику – успеваемость.

Модифицируем модели, используя систему целевых дидактических показателей, предложенных В.П. Беспалько. Она менее детальна и более алгоритмична, чем таксономия Блума, реализованная в SCORM, и в большей степени подходит к электронному обучению.

У В.П. Беспалько выделено несколько характеристик, но мы будем использовать только одну характеристику - «степень автоматизации». Этот показатель характеризует умения как навыки в овладении осваиваемыми способами деятельности, что иногда требуется в процессе обучения. Можно измерять степень автоматизации усвоения коэффициентом:

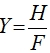
где H - время выполнения теста профессионалом; F - время выполнения теста учащимся.

Считается, что если  то это хороший результат. В некоторых областях (подготовка летчика, водителя, хирурга и т.д.) должно выполняться условие .

Следовательно, можно после прохождения теста оценивать степень автоматизации обучающегося, например, по вышеприведенной формуле. Для этого необходимо произвести модификацию моделей предметных и персональных знаний.

В связи с этим, каждая вершина q_i графа будет взвешиваться вектором , H – время прохождения профессионалом. Состав и структуру предметных знаний отражает нечеткий ориентированный граф Error! Objects cannot be created from editing field codes., представленном на рисунке 1.

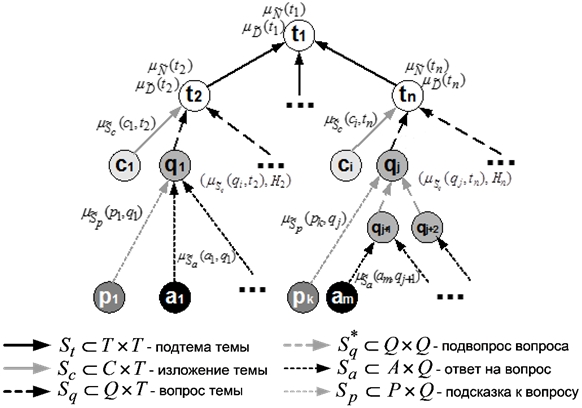
Рис. 1 – Модифицированная модель предметных знаний

 

Вершины графа отражают состав предметных знаний – множество E предметных элементов (ПЭ). Дуги графа отображают  антирефлексивное, ассиметричное и транзитивное бинарное отношение , характеризующее структуру предметных знаний. Вершины и дуги маркированы значениями функций принадлежности нечетких множеств и отношений, отражающих представления эксперта об учебном предмете на качественном уровне ­и выделенных с учетом системы дидактических показателей Беспалько В.П. Функции принадлежности данных нечетких множеств и отношений формируются экспертом перечислением, что обусловлено тем, что их носители дискретны и  мощность их относительно невелика. Фактор-множество вершин графа , порожденное разбиением по функциональному признаку, определяет необходимые таблицы  базы данных КОС, в которых хранятся заданные экспертом функции принадлежности выделенных нечетких множеств и отношений. Фактор-множество связей графа , порожденное разбиением по смысловой нагрузке структурной связи ПЭ, устанавливает связи данных таблиц.

Из этого следует что в модели персональных знаний каждая вершина  графа будет взвешиваться вектором , где F – время прохождения теста студентом. Состав и структуру персональных знаний отражает нечеткий ориентированный граф , изображенный на рисунке 2.

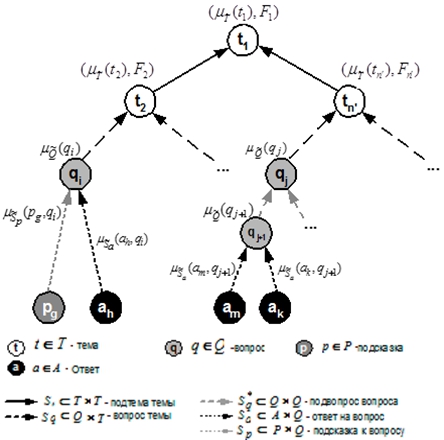
Рис. 2 – Модифицированная модель персональных знаний

Вершины графа  отражают состав диагностированных предметных знаний - подмножество ; дуги графа  отражают структуру диагностированных предметных знаний - подотношение . Дуги графа маркированы значениями функций принадлежности выделенных выше нечетких отношений. Маркировка вершин определяется в результате построения нечетких подмножеств множества E, последовательно обуславливающих друг друга:

где   - нечеткое множество, характеризующее степень знания вопроса;  - нечеткое множество, характеризующее степень незнания вопроса;  - нечеткое множество, отражающее оценку уровня владения вопросом учащимся;  -  нечеткое множество, отражающее оценку степени освоения учащимся материала темы;  - обозначение операции индуцирования в average-форме;  - обозначение операции индуцирования в форме граничного объединения. Такое определение функций принадлежности вышеперечисленных нечетких множеств отражает традиционную практику оценивания и повышает степень полноты и достоверности оценки подготовки обучаемого благодаря учету всех факторов, влияющих на ответ учащегося, и, что самое важное, степени их влияния. Фактор-множество вершин графа  определяет таблицы базы нечетких данных, в которых хранятся функции принадлежности выделенных нечетких множеств и отношений, фактор-множество связей графа   отражает связи данных таблиц.

Далее зная H – время ответа на вопрос затраченное профессионалом и F – время затраченное студентом, можно измерить коэффициент степени автоматизации усвоения учебного материала.

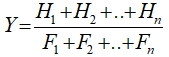
Так как студент может проходить одни и те же тесты неоднократно, то Y будет представлено в виде масcива элементов:

где a – номер теста по теме, b – сколько тестов пройдено.

В соответствии с указанной целью в Пензенском государственном университете (ПГУ) разрабатывается электронный учебный курс (ЭУК) по курсу моделирования систем. В плане структурной организации ЭУК представляет собой совокупность программных компьютерных средств для теоретической и практической подготовки по указанной дисциплине. Для реализации ЭУК использовались языки HTML, ActionScript, С#.

Литература

1. Денисова И.Ю., Князев В.Н., Левашко В.В. Применение мультимедийных технологий при проектировании электронного учебного пособия по курсу "Моделирование систем" на базе нечеткологической математической модели. // Труды VI Международной научно-практической конференции "Молодежь. Наука. Инновации". – Пенза, Издательство Пензенского филиала РГУИТП, 2013. – C.152-154.
2. Балашова И.Ю., Князев В.Н., Левашко В.В. Современные модели представления знаний в компьютерной обучающей системе. // Региональный молодежный форум «Открытые инновации – вклад молодежи в развитие региона». – Пенза, Издательство ПГУ, 2013. – C.30-33.