ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ И ФОРМ КОЛЕБАНИЙ ЛОПАТКИ МКЭ

Секачёв А.Ф.¹, Агарин М.Ю.²

^1,2,Омский государственный технический университет, г. Омск

ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ И ФОРМ КОЛЕБАНИЙ ЛОПАТКИ МКЭ

Аннотация

МКЭ были определены собственные частоты и формы колебаний лопатки цельнолитого диска вентилятора для двух случаев. Первый случай: условия испытания (тензометрирования), второй: условия эксплуатации (наличие центробежных сил, изменяющих жесткость лопатки).

Ключевые слова: собственные частоты, формы колебаний, МКЭ.

Sekachev A.F.¹, Again M.Y.²

^1,2Omskiy state technical University, Omsk

 THE DEFINITION OF NATURAL FREQUENCIES AND MODE SHAPES OF BLADES FEM

Abstract

FEM were identified natural frequencies and mode shapes of blades of solid disk fan for two cases. First case: test conditions (tenzometricheskie), the second: the operating conditions (presence of centrifugal forces that change the rigidity of the shoulder blade).

Keywords: natural frequency, mode shapes, FEM.

Частоты свободных колебаний системы тесно связаны с соответствующими собственными формами. Форма колебаний низшей частоты, как правило, очевидна [1]. Маятник,  к примеру, остаётся практически прямолинейным, для более сложного геометрического тела – лопатки – первая форма это изгибные колебания.

Формы и частоты колебаний являются неотъемлемыми параметрами системы. Их необходимо определять на этапе проработки конструкции, чтобы избежать разрушения при испытании. В случае лопатки, аналитические формулы дают приближенный результат; МКЭ более точно. Также МКЭ достаточно просто позволяет учесть изменение жесткости лопатки от действия центробежных сил.

Расчет частот и форм собственных колебаний лопатки проведен для  частоты вращения n = 5894 об/мин и  при отсутствии вращения. Модель разбивалась 372478 элементов. Количество узлов 76567. Граничные условия – отсутствие перемещений основания лопатки.

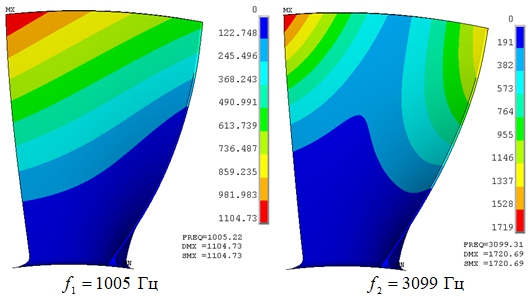
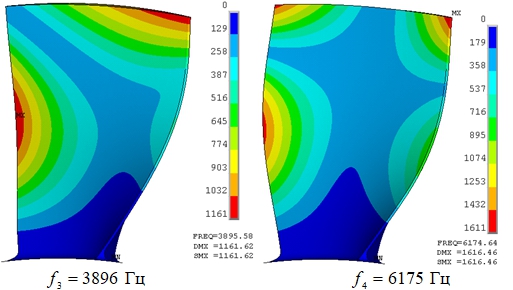
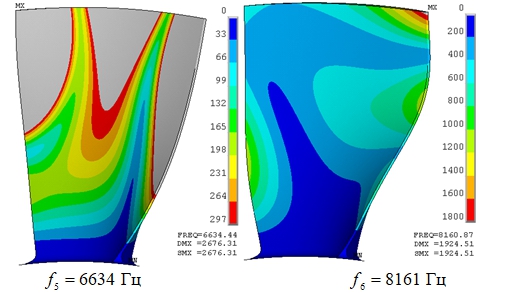
Рассчитаны шестнадцать форм и частот колебаний лопатки в диапазоне 0..20000 Гц. Результаты представлены в таблице. Шесть первых форм собственных колебаний при n = 5894 об/мин изображены на рисунке 1. Первая форма – первая изгибная форма колебаний лопатки. Вторая форма – первая крутильная форма. Третья, четвертая и шестая сложные изгибно-крутильные формы. Пятая – это вторая крутильная.

№ формы	f, Гц (n = 0 об/мин)	f, Гц (n = 5894 об/мин)
1	987,87	1005,2
2	3092,8	3099,3
3	3882,4	3895,6
4	6166,1	6174,6
5	6632,1	6634,4
6	8151	8160,9
7	9407	9418,4
8	10293	10303
9	11523	11532
10	12273	12276
11	14499	14512
12	15488	15496
13	15760	15775
14	16566	16574
15	18603	18601
16	19683	19684

Поскольку, размеры лопатки имеют допуски на изготовления, фактические частоты форм колебаний могут отличаться порядка 5%.

При тензометрировании лопаток место наклейки тензорезистора должно быть выбрано так, чтобы он был чувствителен к колебаниям и по первой и по второй форме.

Действие центробежных сил при частоте вращения n = 5894 об/мин не значительно увеличило жесткость, о чем свидетельствует не значительное увеличение частот. Тем не менее, МКЭ позволил определить собственные частоты лопатки, которые должны быть подтверждены на испытании, а также фактические частоты, которые будут иметь важнейшее значение для оценки работоспособности вентилятора.

 

Рис. 1 – Формы колебаний лопаток при n = 5894 об/мин

Литература

1. Колебания. Р.Е. Бишоп, Перевод с английского, Главная редакция физико-математической литературы Изд-ва «Наука», 1968 г., 161 стр.
2. Каплун А. Б., Морозов Е. М., Олферьева М. А. ANSYS в руках инженера: Практическое руководство. – М.: Едиториал УРСС, 2003. – 272 с.
3. Басов К. А. ANSYS: справочник пользователя. – М.:ДМК Пресс, 2005. – 640 с.
4. Чигарев А.В., Кравчук А.С. Смалюк А.Ф. ANSYS для инженеров: Справ. Пособие. М.: Машиностроение-1, 2004. – 512с.