НАХОЖДЕНИЕ ОПТИМАЛЬНОЙ СТРАТЕГИИ ФУНКЦИОНИРОВАНИЯ МНОГОНОМЕНКЛАТУРНОГО ПИЩЕВОГО ПРЕДПРИЯТИЯ С ИСПОЛЬЗОВАНИЕМ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ И МЕТОДА РОЯ ЧАСТИЦ

Научная статья

Остроух Е.Н.

Солопова О.Г.

Кулешова Е.Ю.

Выпуск: № 5 (24), 2014

Опубликована:

2014/06/08

PDF

Остроух Е.Н.¹, Солопова О.Г.², Кулешова Е.Ю³

¹Доцент, Донской государственный технический университет, кандидат технических наук, доцент (ДГТУ, г. Ростов-на-Дону); ²Доцент, Ростовский государственный экономический университет, кандидат технических наук, доцент (РГЭУ, г. Ростов-на-Дону); ³Магистрант, Донской государственный технический университет, (ДГТУ, г. Ростов-на-Дону)

НАХОЖДЕНИЕ ОПТИМАЛЬНОЙ СТРАТЕГИИ ФУНКЦИОНИРОВАНИЯ МНОГОНОМЕНКЛАТУРНОГО ПИЩЕВОГО ПРЕДПРИЯТИЯ С ИСПОЛЬЗОВАНИЕМ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ И МЕТОДА РОЯ ЧАСТИЦ

Аннотация

В данной работе предложена оптимизационная постановка задачи управления функционированием предприятия, выпускающего пищевую продукцию с большой номенклатурой наименований, поставленная в форме задачи нелинейного программирования с векторным критерием, для решения которой разработан модифицированный генетический алгоритм, а также один из инновационных эвристических методов-метод роя частиц. Разработан программный продукт, применяющий два алгоритма оптимизации на выбор пользователя – генетический алгоритм или алгоритм роя частиц.

Ключевые слова: нелинейное программирование, генетический алгоритм, стратегия управления.

Ostrouh E.N,¹, Solopova O.G.², Kuleshova E.U.³

¹Professor of department, Don state technical University, candidate of technical

Siences (DSTU, Rostov on Don),

²Professor of department, Rostov state economic University , candidate of technical Siences (RSEU, Rostov on Don),

³Undergraduate of Don state technical University (DSTU, Rostov on Don)

OPTIMAL STRATEGIES MULTIPRODUCT FOOD BUSINESSOPERATION USING GENETIC ALGORITHMS AND PARTICLE SVARM

Abstract

In this paper the authors propose an optimization problem of control over the operation of the company, which produces food products with a large range of items delivered in the form of a nonlinear programming problem with a vector criterion, for which we have developed a modified genetic algorithm, and also one of the innovative heuristic methods, particle swarm optimization. The developed software using two algorithms of optimization on the user selection - genetic algorithm or particle swarm optimization algorithm.

Keywords: nonlinear programming, genetic algorithms, management strategy.

Итак, рассматривается задача выбора оптимальной стратегии управления малым предприятием, имеющим дефицит финансовых ресурсов с учётом договорных обязательств и сезонности спроса на продукцию.

Решив её, получаем оптимальную стратегию управления предприятием на данный момент времени (изменение номенклатуры изделий, введение инновационных технологий и т.д.).

Математическая модель задачи имеет следующий вид:

(1)

где: C_i – удельная прибыль от продажи единицы продукции, т.е., разница между доходом и затратами: на приобретение сырья - Z₁, транспортировки - Z₂, хранения на складе - Z₃, налогообложение- Z_4.

Исходя, например, из прибыли минимум в 25 %, имеем:

C_i=1,25 (Z₁+Z₂+Z₃+Z₄) (2)

(3)

где b_i, i=1_…n– удельные издержки на транспортировку и хранение продукции;

(4)

где – экологические издержки при производстве;

(5)

где – удельная отпускная цена единицы товара;

A – розничная цена (цена в розничном магазине).

(6)

где A1 – оборотный капитал (на закупку, транспортировку и хранение продукции);

(7)

где – затраты на издержки:

М=0,15×A₁, (8)

A+M= A₁, (9)

α_i≤x_i≤β_i , (10)

где α_i – договорные обязательства с постоянными заказчиками на продукцию x_i;

β_i– максимальный спрос на продукцию x_i;

x_i≥0 (11)

Многокритериальная задача (1), (3)-(5), (7), (10)-(11) может быть сведена к однокритериальной. Обозначим критерии (1), (3), (4) как F1, F2, F3 соответственно.

Тогда целевая функция принимает вид:

α F₁-β F₂-γ F₃→ max (12)

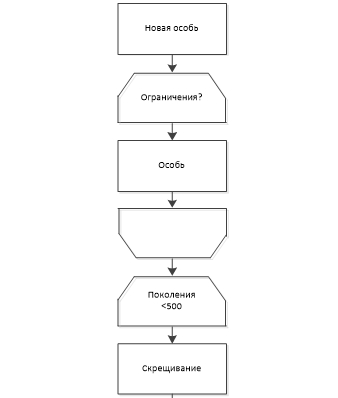
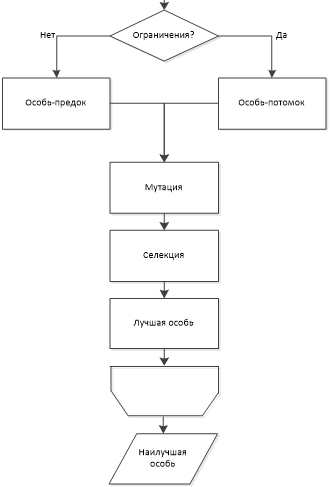
Поставленная задача весьма специфична и использование классического генетического алгоритма весьма затруднительно, поэтому была проведена некоторая модификация классического алгоритма и получен модифицированный генетический алгоритм (рис.1), достаточно эффективно решающий сформулированную задачу. В отличие от классического алгоритма, при генерации каждой особи необходимо проверять её «живучесть», т.е. удовлетворяет ли особь поставленным ограничениям. При мутации и скрещивании ограничения не учитываются. Подвергаться процессу мутации может любая особь, у которой вероятность мутации выше 49%. В скрещивании могут участвовать любые пары особей. Выбор особей, которые будут скрещиваться, происходит случайным образом из всего поколения. Фактически, любая особь может скреститься с любой другой. Некоторые особи могут поучаствовать в размножении не один раз. Формирование нового поколения происходит с учетом ограничений. Если окажется, что какая-либо новая особь не удовлетворяет ограничениям, то она выбрасывается из нового поколения. Недостающее число особей генерируется с учетом ограничений. Это гарантирует, что в каждом новом поколении будут находиться исключительно особи, которые удовлетворяют всем ограничениям. Ещё одним отличием является то, что количество поколений заранее фиксировано, т.е., идёт до указанного числа, и наилучшее решение будет получено при генерации всех поколений. Это неудобство возникло из-за того, что невозможно заранее предсказать желаемую прибыль. Так как классический генетический метод даёт сходимость в среднем за 500 итераций (поколений), то и в данной задаче было принято решение углубиться до 500 поколений. В каждом поколении существует 100 особей.

Блок-схема алгоритма представлена на рисунке 1.

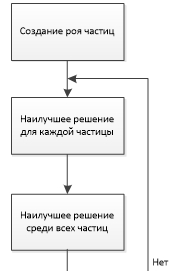
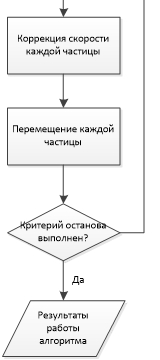
Эта же задача была решена с использованием метода роя.

Блок-схема алгоритма представлена на рисунке 2.

Простой и эффективный путь подбора параметров метода роя предложен Педерсеном и другими авторами [1-2]. Они же провели численные эксперименты с учетом различного типа критериев оптимальности и ограничений для «настройки» параметров МРЧ.

Проведенные по данным алгоритмам вычисления решения конкретно поставленной задачи с нелинейными ограничениями дали схожие результаты, практически не отличающиеся друг от друга.

Результатом выполнения работы является программный продукт, который позволяет получить оптимальную стратегию работы малого предприятия. Стратегия управления учитывает три критерия: доход, издержки и экологичность производства.

Рис. 1 – Блок схема модифицированного генетического алгоритма

Рис. 2 – Блок схема алгоритма роя частиц

Было показано, что разработанная модель, благодаря учёту при расчетах экологической составляющей, обеспечивает наиболее безопасную и экологичную работу любого малого предприятия.

Литература

Алгоритм роя частиц [Электронный ресурс] – URL:http://ru.wikipedia.org/wiki/Алгоритм_роя_частиц
Алгоритм роя частиц [Электронный ресурс] – URL: http://habrahabr.ru/post/105639/