МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ГИДРАТООБРАЗОВАНИЯ В ПОЛИМЕРНОМ АРМИРОВАННОМ ТРУБОПРОВОДЕ МАЛОГО ДИАМЕТРА
Сухоносов А.Л.1, Людвиницкая А.Р.2, Джафаров Р.Д.3
1Кандидат физико-математических наук, доцент, Уфимский государственный авиационный университет; 2кандидат технических наук, доцент, Уфимский государственный нефтяной технический университет; 3аспирант
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ГИДРАТООБРАЗОВАНИЯ В ПОЛИМЕРНОМ АРМИРОВАННОМ ТРУБОПРОВОДЕ МАЛОГО ДИАМЕТРА
Аннотация
Рассмотрена технология отвода газа из-подпакера по полимерному армированному трубопроводу, математически смоделирован процесс гидратообразования в трубопроводе малого диаметра.
Ключевые слова: пакер, скважина, обводненная нефть, газовый фактор, полимерный армированный трубопровод, отвод газа, гидратообразование.
Suhonocov A.L.1, Lyudvinitskaya A.R.2, Dgafarov R.D.3
1PhD in Physics and mathematics, assosiate professor, Ufa State Aviation Technical University (USATU);2PhD, assosiate professor, Ufa State Petroleum Technical University; 3postgraduate stuent
MATHEMATICAL MODELING OF HYDRATE FORMATION IN POLYMERIC REINFORCED SMALL DIAMETER PIPELINES
Abstract
Authors describe a new technique, using an armored polymer pipeas a bypass to flow out excessive natural gas, othervise aggregating under a production packer. Authors also introduce a new mathematical model describing hydrates creation in small-diameter pipes.
Keywords: Packer, wellbore, high-watercut oil production, gas factor, armored polymer pipe, exsessive natural gas removal, hydrates creation.
При использовании пакерной компоновки с полимерным армированным трубопроводом для отвода газа из-подпакерной области по трубопроводу отводится влажный газ, поэтому возникает опасность отложения гидратов, особенно в интервалах вечной мерзлоты. В области локального понижения температуры возникают условия для гидратообразования.
Нами была рассмотрена задача по определению скорости образования гидратного слоя и области возможного локального ускорения потока газа. Для получения модели принималось что газ, выделяющийся из нефти – метан. Рассматривалось одномерное движение влагонасыщенного газа в трубке внутренним радиусом ![]() и внешним
и внешним ![]() . Считается, что влаги, необходимой для образования гидрата, достаточно по всей оси трубки, так что проходное сечение
. Считается, что влаги, необходимой для образования гидрата, достаточно по всей оси трубки, так что проходное сечение ![]() и диаметр
и диаметр ![]() полагаются переменными относительно пространственной координаты и времени. Здесь
полагаются переменными относительно пространственной координаты и времени. Здесь ![]() – толщина слоя гидрата в трубке.
– толщина слоя гидрата в трубке.
Процесс гидратообразования идет медленно, по сравнению со скоростью установления температуры и давления газа, так что процесс можно считать квазистатическим, а давление и температура газа описываются системой уравнений:
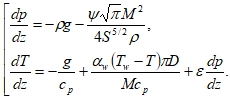 (1)
(1)
Здесь координата z отсчитывается вдоль оси трубки, g – ускорение свободного падения, p – плотность газа, ![]() – постоянный массовый расход газа (v –скорость потока),
– постоянный массовый расход газа (v –скорость потока), ![]() – удельная теплоемкость газа при постоянном давлении,Ψ – коэффициент гидравлического сопротивления, ε – коэффициент Джоуля-Томсона.
– удельная теплоемкость газа при постоянном давлении,Ψ – коэффициент гидравлического сопротивления, ε – коэффициент Джоуля-Томсона.
Для системы (1) задаются начальные условия
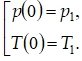 (2)
(2)
где ![]() – давление и температура на входе в трубопровод.
– давление и температура на входе в трубопровод.
Система (6) дополняется уравнением состояния:
![]() , (3)
, (3)
где коэффициент сверхсжимаемости газа задается уравнением Латонова-Гуревича:
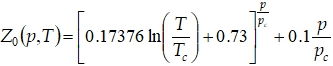 (4)
(4)
Температура стенки ![]() для областей, покрытых гидратом, принимается
для областей, покрытых гидратом, принимается ![]() . Температура
. Температура ![]() фазового перехода газ-гидрат определяется уравнением
фазового перехода газ-гидрат определяется уравнением
![]() , (5)
, (5)
где ![]() - эмпирические постоянные.
- эмпирические постоянные.
Для областей свободных от гидрата температура стенки канала ![]() определяется из решения тепловой задачи для распределения температуры
определяется из решения тепловой задачи для распределения температуры ![]() в толще материала трубки, т.е.
в толще материала трубки, т.е. ![]() , где
, где ![]() – внутренний радиус трубки. Заметим, что тепломассоперенос через канал трубопровода достаточно мал по сравнению с тепломассопереносом в скважине, так что можно принять, что поток газа в трубопроводе практически не влияет на температурное поле.
– внутренний радиус трубки. Заметим, что тепломассоперенос через канал трубопровода достаточно мал по сравнению с тепломассопереносом в скважине, так что можно принять, что поток газа в трубопроводе практически не влияет на температурное поле.
На границе раздела фаз, следуя [1-3], запишем условие Стефана в виде:
![]() (6)
(6)
Здесь ![]() − плотность гидрата, удельная скрытая теплота образования гидрата, коэффициент теплопроводности гидрата,
− плотность гидрата, удельная скрытая теплота образования гидрата, коэффициент теплопроводности гидрата, ![]() − коэффициент теплоотдачи от газа к гидратному слою,
− коэффициент теплоотдачи от газа к гидратному слою, ![]() − температура гидрата, T − температура газа в канале,
− температура гидрата, T − температура газа в канале, ![]() − толщина гидратного слоя. Уравнение (1) выражает тот факт, что скорость гидратообразования определяется интенсивностью тепловых потоков к фазовому фронту, как со стороны стенки канала, так и со стороны газа. Координата r − радиус-вектор, выходящий из точки на оси канала в горизонтальном направлении.
− толщина гидратного слоя. Уравнение (1) выражает тот факт, что скорость гидратообразования определяется интенсивностью тепловых потоков к фазовому фронту, как со стороны стенки канала, так и со стороны газа. Координата r − радиус-вектор, выходящий из точки на оси канала в горизонтальном направлении.
На внешней и на внутренней стенке трубопровода, в отсутствии гидратного слоя, задаютсяграничные условия третьего рода:
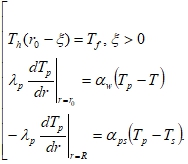 (7)
(7)
Здесь ![]() − температура материала стенки трубки,
− температура материала стенки трубки, ![]() − температура окружающей среды затрубного пространства, распределение которой вдоль вертикальной оси считается заданным,
− температура окружающей среды затрубного пространства, распределение которой вдоль вертикальной оси считается заданным, ![]() − коэффициент теплообмена стенки с окружающей средой,
− коэффициент теплообмена стенки с окружающей средой, ![]() − коэффициент теплообмена стенки трубки с газом в канале,
− коэффициент теплообмена стенки трубки с газом в канале, ![]() − теплопроводность полипропилена.
− теплопроводность полипропилена.
Учитывая анализ, проведенный в [1], примем, что движение фазового фронта происходит достаточно медленно, чтобы считать температурное поле установившимся в любой момент времени. Тогда, решая стационарное уравнение теплопроводности, для участков непокрытых гидратом найдем температуру внутренней стенки трубки:
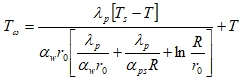 . (8)
. (8)
Для участков покрытых гидратным слоем, из условия Стефана (12) и стационарного уравнения теплопроводности найдем уравнение движения фазового фронта:
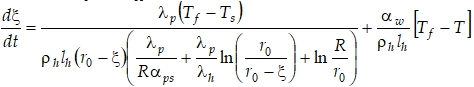 . (9)
. (9)
Таким образом, на каждом временном слое, из уравнений газовой динамики (1) находим распределение давления и температуры в потоке, и, пробегая вдоль оси трубки, определяем распределение толщины гидратного слоя из уравнения (9) и температуру внутренней стенки трубки из соотношения (8).
Литература
- Бондарев Э.А., Габышева Л.Н., Каниболотский М.А. Моделирование образования гидратов при движении газа втрубах // Изв. АН СССР. Механика жидкости и газа, 1982,№ 5, с. 105–112.
- Хайруллин М.Х., Шамсиев М.Н., Морозов П.Е., Тулупов Л.А. Моделирование гидратообразования в стволе вертикальной газовой скважины // Вычисл. технологии,2008, т. 13, № 5, с. 88–94.
- К.К. Аргунова, Э.А. Бондарев, И.И. Рожин. Математические модели образования гидратов в газовых скважинах. Криосфера Земли, 2011, т. XV, № 2, с. 65–69
